《基于变换域的压缩感知快速重构算法》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于变换域的压缩感知快速重构算法

范文

唐川雁史姣姣

摘要：压缩感知是信号处理领域热门研究课题，其应用前提为原信号是稀疏或可压缩的。时域非稀疏信号可以变换为频域稀疏信号，但变换后的信号和传感矩阵表示形式为复数，增加了重构复杂度。为了降低复杂度，提高信号重构效率，提出一种基于实变换的重构算法，该算法将复数形式的稀疏信号和传感矩阵的实部和虚部分离后再参与重构。与传统重构算法相比，该算法改善了重构信号的均方误差，明显缩短了重构时间，极大提高了信号重构效率。

关键词：压缩感知;频域分析;稀疏信号;传感矩阵;实变换;重构算法

DOI：10. 11907/rjdk. 182596 开放科学（资源服务）标识码（OSID）：

中图分类号：TP312文献标识码：A 文章编号：1672-7800（2019）007-0096-04

Fast Reconstruction Algorithm Based on Transformation Domain

for Compressed Sensing

TANG Chuan-yan，SHI Jiao-jiao

（School of Communication Engineering，Hangzhou Dianzi University，Hangzhou 310018，China）

Abstract： Compressed Sensing is a hot research theory in the field of signal processing in recent years.Its application precondition is that the original signal is sparse or compressible.Time domain non-sparse signals can be transformed into frequency domain sparse signals，but the transformed signal and sensor matrix are expressed in the complex number? increasing the complexity of reconstruction.In order to reduce complexity and improve the efficiency of signal reconstruction， a reconstruction algorithm based on real transformation is proposed.The algorithm separates the real and imaginary parts of complex sparse signal and sensor matrix，then participating in the reconstruction operation.Experiments show that compared with the traditional reconstruction algorithms， the proposed algorithm improves the mean square error of reconstructed signal，shortens the reconstruction time and greatly improves the efficiency of signal reconstruction.

Key Words： compressed sensing;frequency domain analysis;sparse signal;sensor matrix;real transformation; reconstruction algorithm

作者简介：唐川雁（1993-），女，杭州电子科技大学通信工程学院硕士研究生，研究方向为信号处理;史姣姣（1992-），女，杭州电子科技大学通信工程学院硕士研究生，研究方向为无线电软件。

0 引言

压缩感知（Compressed Sensing，CS）理论[1-3]自2006年诞生以来发展迅猛，已应用在图像处理[4]、视频编码[5]、信道估计与信道编码[6-7]、目标跟踪[8-9]、模式识别[10]等诸多领域。基于经典奈奎斯特采样定理[11]提出的压缩感知理论，以低于奈奎斯特采样定理要求的频率对信号进行采样，并在采样的同时实现数据压缩。但是该理论的前提是信号在时域必须是稀疏的，或经过某种变换在其它变换域是稀疏的，如离散小波变换、离散余弦变换、离散傅里叶变换等。在此条件下，利用测量矩阵对信号进行降维处理后得到测量矢量，再选择恰当的重构算法即可从测量值中恢复原信号[12]。在这个过程中，测量矩阵与稀疏基相乘后可得传感矩阵，而后续信号重构正是由传感矩阵与测量矢量在迭代过程中匹配最佳原子来逼近原信号以求得稀疏解，再将其与变换基相乘得到最终的恢复信号，因此传感矩阵和稀疏信号影响信号重构的复杂度。该过程求解是一个复杂的组合问题，很难找到满足要求的最优解，一般都是求解其次优解。目前已有许多重构算法可以保证求出次优解，如梯度投影（Gradient Projection For Sparse Reconstruction，GPSR）算法[13]、迭代硬閾值（Iterative Hard Thresholding，IHT）算法[14]、正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法[15-16]、压缩采样匹配追踪（Compressive Sampling MP，CoSaMP）算法[17]、正则化正交匹配追踪（Regularized Orthogonal Matching Pursuit，ROMP）算法[18]、分段式正交匹配追踪（Stagewise OMP，StOMP）算法[19]等。最为经典的OMP算法在余量更新阶段采用Schmidt正交化处理方法使当前原子与已选原子均正交，避免了原子的重复选择，因此OMP算法的收敛过程更快，信号重建效果更好。然而OMP算法在每次迭代过程中都要进行Schmidt正交化处理，使运算量加大，且在迭代过程中每次只选择一个原子，对于大规模问题花费时间较长。而IHT算法较为简单、易于实现，在实际中应用较多，但其易受测量矩阵限制，计算复杂度高、运算时间长。

为克服上述算法的不足，学者Nouasria & Et-Tolba[20]通过传感矩阵乘以逆稀疏矩阵改善重建信号性能，而本文旨在降低时域非稀疏信号转换为频域稀疏信号后以复数形式增加的重构复杂度，将得到的频域稀疏信号和复数传感矩阵以实数形式表现，从而在一定程度上减少误差及算法运算时间，加快算法收敛速度。

1 压缩感知理论

设在[RN]空间中存在一个长度为[N]的离散信号[x]，可看作是一个[N×1]维的列向量。现假设有一组基函数[ψi（i=1，2，？，N）]也是[N×1]维的，若[x]可用[ψi]的线性组合表示，令[Ψ=[ψ1，ψ2，？，ψN]]，则[x]可表示为：

[x=Ψα=i=1Nψiαi] （1）

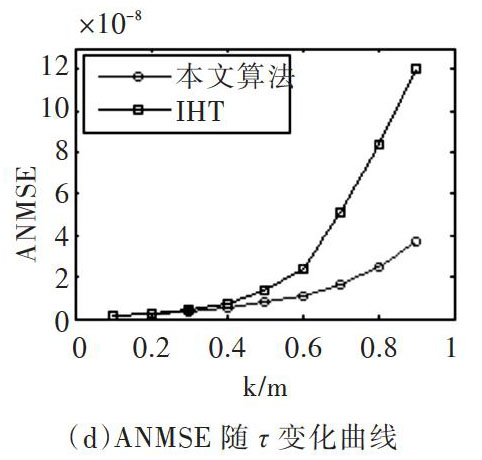
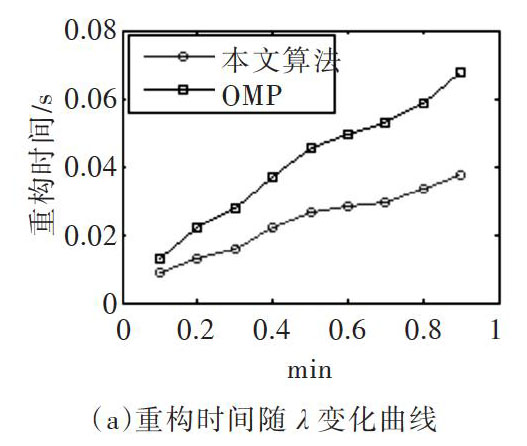
式（1）中，[Ψ]为稀疏基（变换基），[α=[α1，α2，？，αN]T]称为稀疏矢量。若矢量[α]只存在至多[K]个非零值或重要元素，则可认为该信号在变换基上是稀疏的，稀疏度为[K]。CS通过矩阵[A∈RM×N]对信号[x（x∈RN）]进行观测实现降维处理，其中[K

[y=Ax=Dα] （2）

式（2）中，[D=A×Ψ∈RM×N]为传感矩阵，[A]为测量矩阵。

从测量矢量[y]中重构出原始信号[x]的过程叫作CS恢复过程，即求解式（2）。因为[D]不是一个方阵[（M

通过相关重构算法，如OMP算法、IHT算法，就可利用已知的观测向量[y]和传感矩阵[D]求得稀疏表示向量[α]，进而求出信号[x]。

2 基于CS复域到实域的快速重构算法

2.1 算法原理

在信号重建过程中，测量矩阵与稀疏基相乘后可得传感矩阵，而后续信号重构正是由传感矩阵与测量矢量在迭代过程中匹配最佳原子来逼近原信号以求得稀疏解，再将其与变换基相乘得到最终的恢复信号，因此传感矩阵和稀疏信号影响信号重构的复杂度。本文所提算法的系统框图如图1所示，在恢复过程之前分离传感矩阵和经过稀疏变换的信号虚部，变成实矩阵和实信号以降低算法复杂度。

图1 本文算法模型

设长度为[N]的输入信号[x]为时域非稀疏信号，通过傅里叶变换为频域稀疏信号[xf]：

[xf=Fx] （4）

[x=F-1xf] （5）

再通过测量矩阵[A]获得测量值[y]：

[y=Ax=AF-1xf=Dxf] （6）

然后利用本文算法获得实矩阵[Dreal]和实矢量[xfreal]以降低复杂度，此时测量矢量[y]变为：

[y=Drealxfreal] （7）

由已知的测量矢量[y]和实传感矩阵[Dreal]，再利用某种重构算法即可获得稀疏解[xf]，然后通过逆傅里叶变换获得恢复的原信号[x]。经过此算法后，稀疏信号和传感矩阵由原来的复数形式变为实数形式。而在数据处理中，处理实数比复数更加简单且出错概率小，因此由传感矩阵与测量矢量在迭代过程中匹配最佳原子来逼近原信号求得的稀疏解，其均方误差更小，算法收敛速度更快，减少了重构运行时间。

2.2 数学分析

下面证明从复域到实域的转换可得到同样的观测向量[y]，证明过程如下：

信号恢复过程依赖[D]和[xf]的复杂度，因此，将[D]和[xf]由复域变成实域可改善信号恢复性能。

假设矩阵[D]为[m×n]维，[xf]为[n×1]维，则[m×1]维的观测向量[y]为：

[D=A×F-1=ψ11+jθ11? ？？？？? ？？？ψ1n+jθ1n? ? ? ？？？？? ? ? ? ?？？？？？? ? ?？？？？？？？？？？？？？？？？ψm1+jθm1? ？? ψmn+jθmn] （8）

其中[F-1]为逆傅里叶变换矩阵，[ψmn]为矩阵[D]第m行n列的实部，[θmn]为矩阵[D]第m行n列的虚部。

[xf=（R1+jI1，？，Rn+jIn）T] （9）

[Rn]为稀疏信号[xf]第n行的实部，[In]为稀疏信号[xf]第n行的虚部。得到[D]和[xf]后，由两者相乘便能得到测量矢量[y]，如下所示：

接下来分离[m×n]维复矩阵[D]的实部和虚部得到维度为[m×2n]的实矩阵[Dreal]，分离[n×1]维稀疏信号[xf]的实部和虚部得到维度为[2n×1]维的实稀疏信号[xfreal]：

由以上分析可知，式（10）和式（13）得到同样的观测向量[y]，表明由复域到实域的变换在数学上证明是正确的，并且这种变换在一定程度上降低了误差，这是由于处理实矩阵比复矩阵容易得多，重构时间更短。

3 仿真与分析

本文使用长度为[n=1024]的正弦信號作为输入信号：

[x=0.6sin2π29nt-1.5sin2π100nt+sin2π200nt+]

[0.8sin2π400nt+2sin2π500nt-sin2π600nt] （14）

选择测量矩阵[A]为高斯随机矩阵，将时域非稀疏信号[x]变换为频域稀疏信号[xf]，稀疏度为12，测量向量[y=Ax=AF-1xf]，维度为[m×1]，仿真时取[m=roundλ n]，其中[λ=mn]称为压缩率;变换复矩阵[D=AF-1]为实矩阵[Dreal=[real（D） -imag（D）]]，维度为[m×2n]。变换复向量[xf]为实向量，[xfreal=[real（xf）? imag（xf）]T]维度为[2n×1]，此时测量向量[y=Drealxfreal];用其中一种重构算法重构信号，如IHT算法，得到恢复的稀疏信号[xf=xf（1：n）+ixf（n+1：2n）]，再通过逆傅里叶变换得到估计的正弦信号[x]。

计算平均归一化均方误差（Average Normalized Mean Square Error，ANMSE），表达式为：

[ANMSE=15001500x-x22x22] （15）

为了验证本文算法的有效性，选择高斯随机矩阵作为测量矩阵。重构算法以IHT算法、OMP算法为例，取[m=λn]，其中[λ]称为压缩率且[λ=0.1：0.1：0.9]，分别验证算法的重构时间、平均归一化均方误差随压缩率的变化情况。固定测量值[m=256]，取[k=τm]，其中[k]为标准测量稀疏度且[τ=0.1：0.1：0.9]，验证重构时间、平均归一化均方误差随[τ]的变化情况，每种情况均运行程序500次求平均值。仿真环境为Win10 64位系统Intel奔腾G4560处理器的Matlab2014a，结果如图2、图3所示。

图2 本文算法与IHT算法比较

图3 本文算法与OMP算法比较

由图2（a）可知，随着[λ]值的增大，在重构时间上本文算法比IHT算法优势明显，最大可缩短时间72.59%，是IHT算法所用時间的27.40%。随着[λ]的增大，优势渐不明显，但所用时间总是比IHT算法少。图2（b）中，[τ]较小时本文算法较IHT算法优势不大。但随着[τ]的增大，IHT算法在重构时间上增长很快，而本文算法增长较为缓慢。当[τ=0.9]时，本文算法所用时间比IHT算法少了75.72%。

图2（c）中，本文算法开始与IHT算法相比均方误差相当，当[λ0.7]时小于IHT算法。而图2（d）中，两种算法均方误差均随着[τ]的变化而变化，但本文算法误差更小。图3（a）、图3（b）中，本文算法与OMP算法相比，本文算法的重构时间始终小于OMP算法，最大时间分别减少44.69%和60.82%;图3（c）、图3（d）中，与OMP算法相比，本文算法在重构误差上改善明显。综上所述，本文算法在保证重构误差与原算法相当甚至更小的基础上，极大程度地减少了重构时间，算法收敛速度更快，信号重构效率更高。

4 结语

时域非稀疏信号转换为频域稀疏时，使用傅里叶变换将导致稀疏信号和传感矩阵为复数形式而增加信号重构复杂度和运行时间。本文提出一种由复域到实域的变换方法改善算法性能，通过分离稀疏信号与传感矩阵的实部和虚部降低复杂度，加快算法收敛速度，提高重构效率。与传统算法相比，所提算法在改善均方误差的情况下极大程度减少了重构运行时间，算法收敛速度更快，信号重构效率更高。鉴于本文的变换域只是傅里叶基且只对两种算法进行了比较，其它算法与本文算法的性能比较结果还有待进一步验证。因此，将来要与更多算法进行比较验证，以增加本文算法的普适性和鲁棒性。

参考文献：

[1] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory， 2006， 52（4）：1289-1306.

[2] CANDèS E J. Compressive sampling[J]. Marta Sanz Solé， 2006， 17（2）：1433-1452.

[3] 金坚，谷源涛，梅顺良. 压缩采样技术及其应用[J]. 电子与信息学报， 2010， 32（2）：470-475.

[4] LI Q，HAN Y，DANG J. Image decomposing for inpainting using compressed sensing in dct domain[M]. New York：Springer-Verlag Inc，2014.

[5] 顾莹. 基于压缩感知的分布式视频编解码及其图像超分辨率重建研究[D]. 南京：南京邮电大学， 2011.

[6] NIAZADEH R，GHALEHJEGH S H，BABAIE-ZADEH M，et al. Adaptive and non-adaptive isi sparse channel estimation based on slo and its application in ml sequence-by-sequence equalization[M]. Latent Variable Analysis and Signal Separation. Springer Berlin Heidelberg， 2010：579-587.

[7] CANDES E J， TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory， 2005， 51（12）：4203-4215.

[8] 程中建，李康，谷懿，等. 基于稀疏表达特征选择的压缩感知目标跟踪算法[J]. 软件导刊， 2018（7）：91-96.

[9] 黄庆俊，何儒汉. 基于协方差矩阵的压缩感知跟踪算法[J]. 软件导刊， 2017， 16（4）：31-34.

[10] WRIGHT J， YANG AY， GANESH A， et al. Robust face recognition via sparse representation.[J]. IEEE Trans Pattern Anal Mach Intell， 2009， 31（2）：210-227.

[11] 王世一. 数字信号处理 [M].修订版.北京：北京理工大学出版社， 2006.

[12] 倪加明，孙钦者，陆家明. 一种改进的稀疏度自适应压缩采样匹配追踪算法[J]. 通信技术， 2016， 49（8）：992-996.

[13] FIGUEIREDO M A T， NOWAK R D， WRIGHT S J. Gradient projection for sparse reconstruction： application to compressed sensing and other inverse problems[C]. IEEE Journal of Selected Topics in Signal Processing， IEEE Journal of Selected Topics in Signal Processing， 2007：586 - 597.

[14] BLUMENSATH T， DAVIES M E. Iterative hard thresholding for compressed sensing[J]. Applied & Computational Harmonic Analysis， 2009， 27（3）：265-274.

[15] TROPP J A， GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory， 2007， 53（12）：4655-4666.

[16] PATI Y C， REZAIIFAR R， KRISHNAPRASAD P S. Orthogonal matching pursuit： recursive function approximation with applications to wavelet decomposition[C]. Signals， Systems and Computers， 1993 Conference Record of The Twenty-Seventh Asilomar Conference on. IEEE， 2002：40-44 .

[17] NEEDELL D， TROPP J A. Cosamp： iterative signal recovery from incomplete and inaccurate samples [J]. Applied & Computational Harmonic Analysis， 2008， 26（3）：301-321.

[18] NEEDELL D， VERSHYNIN R. Uniform uncertainty principle and signal recovery via？regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics， 2009， 9（3）：317-334.

[19] DONOHO D L， TSAIG Y， DRORI I， et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory， 2012， 58（2）：1094-1121.

[20] NOUASRIA H，ET-TOLBA M. New sensing approach for compressive sensing using sparsity domain[C].2018 19th IEEE Mediterranean Electrotechnical Conference （MELECON）， Marrakech， 2018：20-24.

[21] CANDèS E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes rendus - Mathématique， 2008， 346（9）：589-592.

（責任编辑：杜能钢）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。