《多指标加权关键边评估模型及应用》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

多指标加权关键边评估模型及应用

范文

侯贺郑伟马林郭亚娟

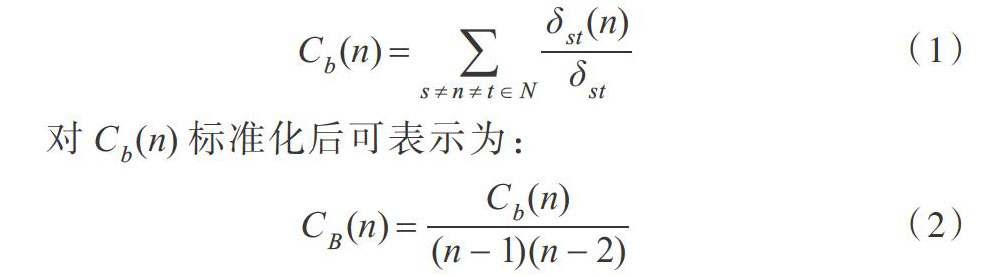
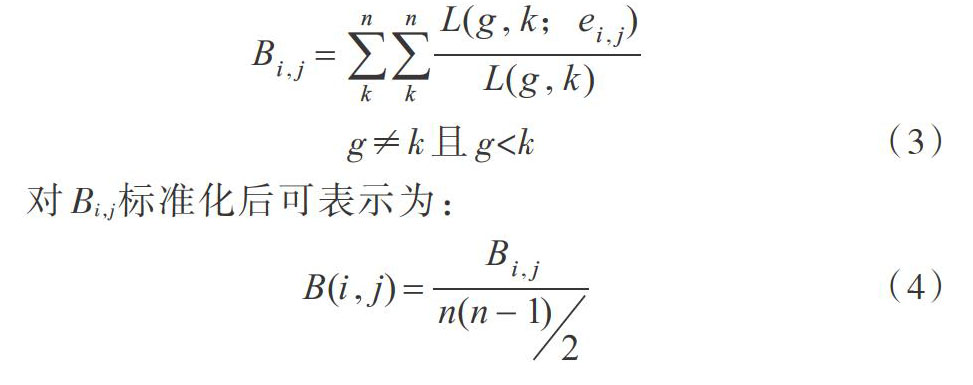
摘要：针对高校网络舆情边评估研究较少、评估指标单一、评估因素特定等问题，提出多指标加权关键边评估模型。首先，将高校网络拓扑化，并利用矩阵表示网络参与者之间的关系;其次，计算网络拓扑中每条边的边介数以及支撑边两个点的点介数;最后，分析在边介数、支撑边两个点的点介数及3个指标的不同加权作用下高校网络中关键边的评估情况。根据多指标加权关键边评估模型，可从网络舆情引导机制、信息工作机制、预警和处理机制4个方面为高校网络舆情引导策略的制定提供参考。

关键词：边介数;点介数;多指标加权;高校网络舆情

DOI：10.11907/rjdk.191043开放科学（资源服务）标识码（OSID）：

中图分类号：TP301文献标识码：A 文章编号：1672-7800（2019）010-0059-03

0引言

根据中国互联网络信息中心（CNNIC）2018年7月份发布的第42次《中国互联网络发展状况统计报告》年龄结构和职业结构分析可知，我国网民主要群体是年龄段为20-29岁的大学生。大学生网民乐于参与互联网话题交流，互联网已成为实现交流的一种重要形式。高校网络作为大学生交流的重要场所，受到了广泛关注和重视，高校网络舆情也成为研究热点。

目前，高校网络舆情研究主要集中在舆论学、系统动力学、社会网络分析学3方面。舆论学从经验总结层面，通过现象定性描述高校网络舆情引导及应对机制，缺乏对网络舆情形成机制、传播机制的研究;系统动力学从因果关系层面，搭建高校网络舆情流图，并构造方程描述流图中每个要素间的定量关系，可实现高校网络舆情形成机制、传播机制的定量分析。然而流图方程中各要素权重均由专家依据主观赋权法评判得出，其主要缺点是权重随机性较大，会因选取专家的不同，得出的权重系数也不同，可能造成网络舆情分析结果与实际差异较大;社会网络分析法将高校网络拓扑化，网络拓扑中的节点表示高校网络中的行动者，边表示高校网络中行动者之间的关系。该方法通过研究网络拓扑中的节点、边的指标值，将高校舆情网络中的行动者及其之间的关系量化，克服了舆论学定性描述和系统动力学主观赋权的缺点，是研究高校网络舆情的一种重要方法。黎友红以高校网络节点为研究对象，根据高校舆论网络中节点的度、介数指标挖掘高校网络中的意见领袖，提出高校应对网络舆情的两种方法;刘欣等综合考虑网络实际情况，采用网络节点的k-shell值、介数值、紧密值3个指标加权挖掘意见领袖，全面分析网络多种节点的作用，优化了意见领袖排序方法。网络节点重要性评估是高校网络舆情研究中的重要内容，但是现有研究往往片面强调节点重要性而忽略边对节点的影响。针对该缺点，熊金石等在充分考虑节点重要性的基础上，引入边介数表征边对节点的支撑作用，建立了节点度与边介数共同作用下的节点重要性评估模型，利用真实网络验证评估模型有效性。相對于社会网络视觉下高校网络舆情中节点边评估方法，高校网络中边的研究未受到太多关注，且现有评估方法较少。常用方法仅将边介数作为衡量边重要性的指标，认为边介数越大边越重要，评估指标单一，结果具有一定的片面性。邱原建立了两个不同结构的网络，验证了边介数相同的两条边在所属网络中的重要度不一定相同，并在此基础上提出一种基于复杂理论的关键边评估方法。该评估方法与直观判断边重要度基本保持一致，但仅考虑了节点度、节点介数、边介数在特定情况下的综合作用，缺乏对多指标加权作用下关键边重要性的研究。

综上所述，本文提出一种多指标加权关键边评估方法，研究边介数及支撑边的两个节点介数在不同权值下的关键边排序，以此为依据对高校网络舆情进行管理引导。

1高校网络拓扑结构

1.1社会网络分析

社会网络由社会行动者及其关系纽带构成网络拓扑，社会网络分析（Social Network Analysis，SNA）是一种基于网络拓扑的多学科交叉研究方法，该方法在社会学、心理学、生物学、统统计学等众多领域得到广泛应用和长足发展。在网络舆情中，网民作为行动者通过对某话题进行点赞、转发、评论等操作彼此连接，网民及其连接共同构成社会网络。作为网络舆情的一种类型，高校网络舆情也可按照社会网络分析法进行研究。

1.2网络拓扑及表示

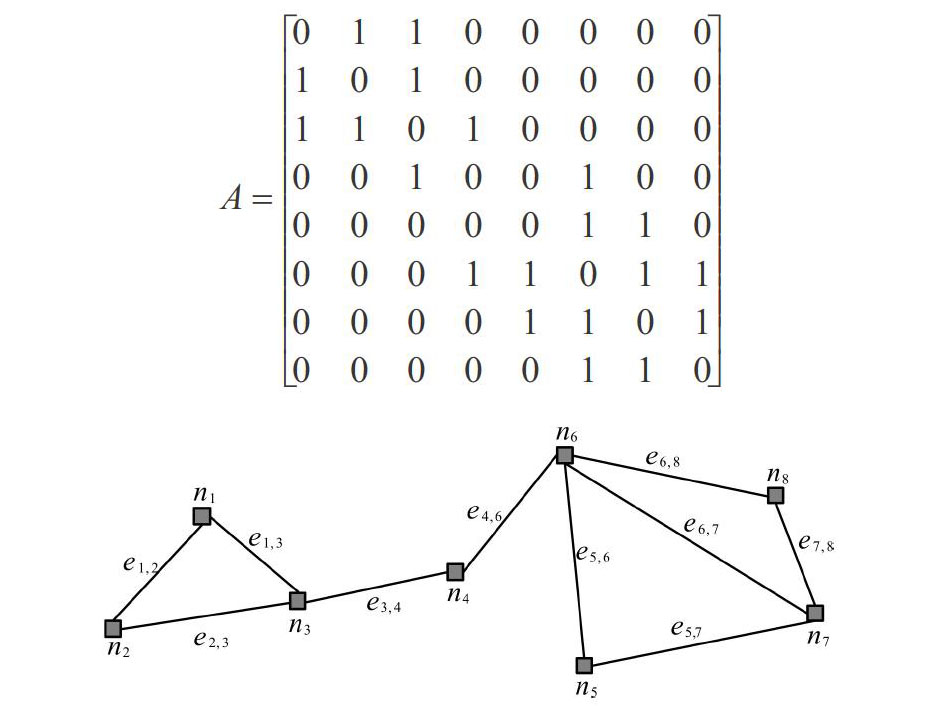
用集合C=（N，E）表示网络拓扑图，其中N={ni|i=1，2，…，}表示节点集合，E={ei，j|i≠j}表示边集合。高校网络舆情针对某个话题构成的一个网络拓扑图如图1所示，ni（i=1，2，3，4，5，6，7，8）表示8个学生节点，ei，j（i≠j）表示节点ni和nj有相关关系。

图1中节点及节点间关系可用邻接矩阵A表示，矩阵的行和列表示节点，矩阵元素值表示两节点之间的关系。如节点n1、n2进行了点赞、转发、评论等互动操作，则对应值为1，邻接矩阵A可表示为：

2多指标加权关键边评估模型

2.1节点介数

节点介数指社会网络图中某一点处于其它点对最短路径上的概率之和。式（1）中，δst表示点s到点t之间存在的最短路径总数，δst（n）表示在网络图中点s到点t之间通过点n的最短路径数目。因此，Cb（n）表示点n处于所有其它点对最短路径的概率和，即n的节点介数。

节点介数是社会网络衡量α节点重要性的指标，表示节点对网络的控制能力，处于任意位置的某个节点最短路径概率较高，则该节点对网络控制能力较强，其信息导向作用更大。

2.2边介数

边介数定义为社会网络中某条路径处于所有其它点对最短路径的概率之和。式（3）中L（g，k）表示节点g和k之间存在的最短路径总数，L（g，k;ei，j）表示存在于节点g和k之间且通过边ei，j的最短路径数目，Bij表示边ei，j处于所有其它点对概率之和，即ei，j的边介数。

边介数是社会网络中衡量路径的重要指标，反映了路径对网络传输及控制能力，若某条路径处于任意节点、最短路径概率较高，则该条路径对网络传输及控制能力较强，在网络中的作用也较大。

2.3多指标加权关键边评估模型

在结构不同的两个网络中，两条路径的边介数相同并不意味着该路径在网络中的重要度一致，因此仅将边介数作为衡量边重要性唯一指标具有一定片面性。网络中边的重要性除与边介数相关外，还依赖于支撑边的两个节点对其产生的影响。因此，将边介数、两个节点介数加权评估网络中边的重要度，从而挖掘网络关键边，其评估结果可能更接近真实情况。因此，多指标加权评估网络关键边数学模型构建如式（5）所示。

2.4关键边评估值计算流程

将网络拓扑化后，用矩阵表示网络参与者及其之间的关系，关键边评估值计算流程为：①根据式（4），确定边ei，j的边介数B（i，j）;②根据式（2），确定节点i的点介数Ci;③根据式（2），确定节点;的点介数Gj;④根据式（5），计算在不同α、β、γ加权下关键边ei，j的评估值Ii，j。

3多指标加权关键边高校网络舆情引导策略

网络作为学生沟通和交流的重要平臺，在高校舆论中发挥重要作用，正确引导网络舆论十分重要。根据多指标加权关键边评估模型，本文提出从以下3个方面进行引导：

（1）健全网络舆论引导机制。通过多指标加权关键边的分析，可以得出高校网络舆情参与者之间的关系，并且在网络舆情中存在重要关系，这对网络舆情引导有重要意义。首先，重要关系在网络舆情的形成中具有枢纽作用，研究高校网络舆情中的重要关系，有助于挖掘网络舆情演化规律，掌握网络舆情发展趋势，制定应对措施;其次，通过重要关系的建立和管理，引导正确的网络舆论。

（2）完善网络舆情信息工作机制。传统网络舆情信息工作机制是专门化的舆情通报机制，由专门部门、专项刊物对日常舆情进行采集、整理、分析，并按照自上而下的层级结构构建而成。在网络舆情信息工作机制建设上，高校还应该重视网络舆情自身优势，以多指标加权关键边为依据，在通报机构和掌握基层舆情信息的参与者之间建立直接通报关系，利用网络舆情传播优势实现网络舆情通报。

（3）提高预警和处置能力。针对敏感话题，利用多指标加权关建边进行网络舆情仿真、分析，总结多种舆情事件一般规律和共同特征，进而对潜在舆情话题进行预测、分析并制定处置预案。

4结语

本文提出的多指标加权评估网络关键边数学模型，综合考虑了边介数、支撑边节点介数等因素，通过具体网络拓扑分析，得出应将边介数作为关键边评估的主要因素，并应结合支撑边节点介数共同对关键边进行评估的结论。因此，在高校网络舆情管理及引导工作中，除要关注网络用户外，还应关注用户之间的关系，并进行引导管理。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。