《合情推理》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

合情推理

范文

张凤玲

【摘要】德国教育家第斯多惠指出：“教育的艺术的本质不在于传授本领，而在于激励、唤醒、鼓舞.”合情推理是启迪学生思维的利器，教师在教学中启发学生用合情推理迁移建模，指引学生用合情推理归纳拓展.

【关键词】合情推理;迁移;数学建模;归纳回顾;拓展

教师创设具体生动的教学情境，唤起学生积极愉快的情感，激活学生的思维，不仅有利于培养学生多种优良思维品质，也体现了“在于激励、唤醒、鼓舞”这种教学艺术.显然，启迪学生思维是教学艺术的主旋律，也是教学艺术的核心，更是数学教学责无旁贷的使命.而合情推理就是启迪小学生思维发展的利器[1].

一、合情推理，迁移利器

古希腊的哲学家苏格拉底这样说过：“教育不是灌输，而是点燃火焰.”教师在教学中若想避免强硬地灌输知识，可以借助合情推理，引导学生把已经学到的知识技能自主地遷移到要学习的新知上.合情推理在不经意间就把教师传授知识变成了学生自主习得新知.在教学“比的基本性质”时，由于在前一节课学生刚刚明确了比、除法、分数三者的对应关系，所以，教师启发学生大胆猜一猜：除法有商不变的性质，即被除数与除数同时乘或除以同一个不为零的数，商不变，而分数也有分数的基本性质，即分数的分子和分母同时乘或除以同一个不为零的数，分数的大小不变.那么，比有没有类似的性质呢？学生利用合情推理很自然地就从这两个熟悉的性质迁移到比的基本性质了，同时，将零散的知识系统化了.在教学“小数的加法”时，教师问：“你们是怎么计算整数加法的？”“将数字的末尾对齐！” “你知道为什么要将数字的末尾对齐吗？”“因为这样数位就对齐了！” “那么小数的加法能不能也像整数的加法那样把末尾对齐呢？为什么？”“不能，因为小数的末尾可能是十分位，也可能是百分位或千分位！”“那该怎样对齐小数的数位呢？”学生马上就想到了对齐小数点，小数点对齐了，个位就对齐了，所有的数位都跟着对齐了.由计算整数加减要末尾对齐合情推理出计算小数加减时要小数点对齐，完成了整数加减法到小数加减法的完美迁移.在教学“圆的面积”时，学生在经历了数出3个边长等于圆的半径的正方形的面积，用数格子的方法数出3个对应圆的面积，计算出每个圆的面积是与边长等于它的半径的正方形的面积的倍数后，启发他们大胆推测圆的面积是边长等于它的半径的正方形的面积的几倍.有了刚刚学过的圆的周长是直径的π倍，而这里反复出现3倍多一点，很容易让他们合情推理出也是π倍.而到论证阶段，学生自然而然地想到以往多边形的面积公式的推导过程，如平行四边形的面积通过剪拼法转化成长方形的方法，那么，是否也可以迁移到把圆的面积通过剪拼法转化成长方形呢？这样的迁移顺利地完成了圆的面积公式的推导，水到渠成，顺理成章.

二、合情推理，建模利器

数学学习的过程在很多时候就是数学建模的过程.在数学建模的过程中，总少不了合情推理的身影[2].在教学“圆柱的体积”时，学生面对这种全新的柱体的体积，很自然地回忆起曾经学习过的两种立体图形的体积——长方体和正方体的体积.它们的体积都可以统一用一个体积公式去求，即体积=底面积×高.学生很自然地推理出圆柱的体积是不是也可以用它的底面积×高去求？再次联想圆的面积公式的推导过程是把圆形转化成长方形，那么，这里的圆柱体是不是也可以用类似的方法转化为长方体？在学生完成证明后，教师让学生思考：是不是所有的柱体的体积都可以统一成这一个体积公式？为什么？学生展开自己的想象和推理，很快得出肯定的结论.如果柱体的底面是平行四边形，可以通过割补法将它变成长方形，原来的柱体变成了长方体;如果柱体的底面是三角形，可以沿着它一边的中位线裁开，再旋转180°得到平行四边形，再重复刚才的割补法将它变成长方形，原来的柱体变成了长方体;如果柱体的底面是其他的多边形，都可以通过若干次割补法将它变成长方形，原来的柱体变成了长方体……所以，学生通过合情推理建立起了他们学习生涯中一个非常重要的数学模型：即柱体的体积=底面积×高.综上所述，合情推理在数学模型建立过程中起到了重要作用：第一次合情推理指引了正确的猜想方向，第二次合情推理找出了正确的证明方法，第三次合情推理构建了数学模型.一次次合情推理闪烁着智慧的光芒，让我们越来越接近事实和真理.在教学“圆锥的体积”时，教师设计了两个实验，引导学生合情推理建立数学模型：一个是教师演示实验，一个是学生实验.实验准备：透明的塑料教具（等底等高的圆锥和圆柱）、一脸盆水、红墨水、一个小圆锥、一个大圆锥.实验过程：出示等底等高的圆锥和圆柱.“同学们，仔细观察老师手中的圆锥和圆柱，想一想，它们的底面积和高有什么关系？”“相等！”“怎么看出来的？”指名让学生演示比较过程，学生把它们的底面重叠在一起“它们的底面积正好重合，所以底面积相等.你看，把它们放在桌面上它们一样高，所以高也相等！”“你真会比，我们称它们是等底等高的圆锥和圆柱，猜一猜，这个圆柱的体积是圆锥的几倍？”“2倍！”“3倍！”“请看！”教师往脸盆里滴了几滴红墨水，再用透明的塑料圆锥装满水，倒入透明的塑料圆柱体中，“看看这里满满一圆锥的水可以到圆柱的几分之几的位置？”“三分之一”“让我们来倒倒看！”“两杯，三杯.三杯倒满，你猜对了吗？”等底等高的圆柱和圆锥体积之间的倍数关系就这样给学生留下了深刻的印象.学生实验就是一个简单的手工，用手中两团颜色不同、大小相同的橡皮泥分别捏成圆柱和圆锥.第一次要求圆柱和圆锥的底面积相同，比较圆柱和圆锥的高.第二次要求圆柱和圆锥的高相同，比较圆柱和圆锥的底面积.学生很快投入到火热的捏橡皮泥的实验中，捏着捏着就会发现：圆柱和圆锥的体积和底面积都相等，就是用同样大的橡皮泥捏出底面积一样的圆柱和圆锥，而圆柱上下一样粗，圆锥是越来越尖，用同样多的橡皮泥捏出圆锥要高许多.轻松得出了第一个结论：体积相等、底面积相等的圆柱和圆锥，圆锥的高是圆柱高的3倍;再用这两团橡皮泥捏出高相等的圆柱和圆锥，不难发现，圆锥的底面积是圆柱高的3倍.于是得出第二个结论：体积相等、高相等的圆柱和圆锥，圆锥的底面积是圆柱的3倍.

三、合情推理，归纳利器

归纳回顾是数学教学中不可忽视的重要环节，俗话说得好：“千金难买回头看.”著名的教育家波利亚也曾指出：“你也许能找到一个更好的新解答，找出新的有趣的事实，无论如何，你如果养成以这种方式回顾和仔细检查你所解答的习惯，你将获得一些条理分明、随时可以使用的知识，并且将会提高你的解题能力.”这些都明确地告诉我们一个道理：解出一道题，不是思考的结束，而是新的思考的开始.

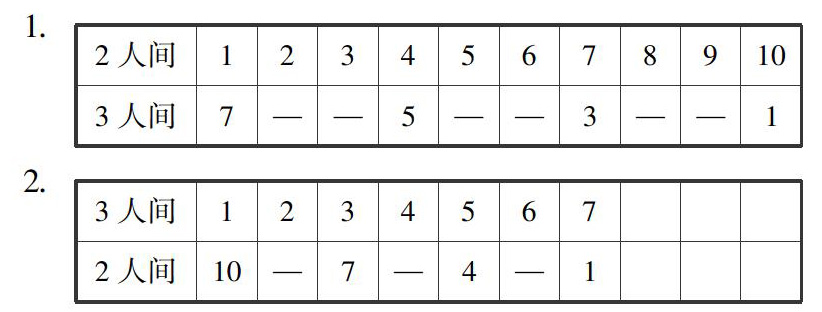
教学例题：旅游团23人到旅馆住宿，住三人间和两人间（每个房间不能有空位），有多少种不同的安排？学生根据上节课所学的一一列举的解决问题的策略，自主解答，展示出以下两种不同的解法：

在教学时，我问学生：“这两种解法，你更喜欢哪一种？”“第二种！”“为什么？”“它的表格短一些！简单些！”“你知道为什么第二种的表短一些吗？”“因为第二种解法，第一行表示的是3人间在逐渐增加，每增加1间就解决了3人的住宿.而第二种解法，第一行表示的是2人间在逐渐增加，每增加1间只能解决2人的住宿.所以第一行是3人间的表格短一些！” “再仔细观察每个表格的第二行，你有什么发现？”“数字的变化好像有规律，第一个表的第二行后面的数总是比前面一个数小2，第二个表的第二行后面的数总是比前面一个数小3！”“这里的小2小3与题目中出现的2人间3人间，数字上的重复是不是偶然？”“不是偶然！因为3个2人间住的人正好住满2个3人间.所以，我们看第一个表的第一行从1变成4表示2人间增加了3个，相应的第一个表第二行的3人间就从7变成5，表示3人间减少了2个：2×3=3×2.所以，这里有四种不同的安排，分别是：1个2人间和7个3人间、4个2人间和5个3人间、7个2人间和3个3人间、10个2人间和1个3人间.”学生还意犹未尽：“弄明白规律之后，其实我们只要找到了第一种，后面三种可以根据2人间每增加3个，3人间就相应地减少2个的规律推出来.”“我还知道这种住房间的题，以后列表时，把住人多的放在第一列，表就相应短一些！”利用合情推理进行归纳，学生收获满满.

四、合情推理，拓展利器

孔子说：“举一隅不以三隅反，则不复也.”意思是：学一件东西，不会灵活地思考，再把学到的方法运用到其他相类似的东西上，这样的学生就没法教了.伟大的教育先圣充分肯定了在学习过程中拓展应用的重要性.而合情推理又是必不可少的拓展利器.学生能熟练地利用合情推理轻松地做到举一反三[3].在学习了六年级下“解决问题的策略”的例题时，学生根据画图的策略找到了解决鸡兔同笼问题的一般性方法——假设法.

例题如下：全班42人去公园划船，租10只船正好坐满.每只大船坐5人，每只小船坐3人.租的大船、小船各有多少只？假设租的全是大船，那么10只大船可坐10×5=50（人），有50个座位，而全班只有42人去划船，坐不满，50-42=8（个），还有8个空座位.所以，要将其中的一部分大船换成小船.每只大船坐5人，每只小船坐3人.5-3=2（个），每将一只大船换成一只小船可以减少2个空座位：8÷2=4（只），要把其中的4只大船换成小船，所以，租的大船：10-4=6（只），租的小船：4只.已知总人数和总共要租的船的只数，还有大小船的满载量，求租的大船、小船的只数.在求解时，可以先假设全是大船或全是小船，再根据假设算出假设的座位，算出与实际人数的差，然后调整最初的假设.在学生做了几道类似的练习之后，出示这样一道思考题：在12张球桌上同时进行乒乓球比赛，双打的比单打的多6人.进行双打和单打比赛的乒乓球各有几张？引导学生思考：“这道题和例题有什么不一样？”“例题告诉了我们总人数，而这道题给出的是双打的比单打的多的人数！”“想一想，这道题能不能也用和例题类似的方法来解决？”师生共同摸索：假设全是双打，双打就是12张桌，单打就是0张桌，双打的比单打的多12×4=48（人），而实际双打的比单打的多6人，假设与实际的差别是48-6=42（人）.问：“这里把双打换成单打是不是抵消了2个人的差别，为什么？”学生经过思索后明确：这里和例题不一样，把一桌双打换成单打，参加双打的就少了4人，同时单打的就多了2人，换一次单打就比双打多出6人，所以多出的42人要换7次，所以进行单打比赛的乒乓球桌有7张，双打的有5张.

利用合情推理，学生成功地把经典的鸡兔同笼问题举一反三拓展到复杂的变式题.“教”的最终目的是“不教”，而合情推理让我们轻松地做到从“教”到“不教”，例题有限，拓展无穷.合情推理，居功至伟.

总结

合情推理在教学时能够启发学生在他们迷茫踯躅时，指引迁移建模的方向，能够带领学生进行恰当归纳拓展，开阔视野，举一反三，触类旁通，不把数学学习拘泥于具体的解题.总之，合情推理是启迪学生思维的利器.运用之妙，存乎一心！

【参考文献】

[1]程雪.小学数学低年级学生审题能力的培养策略[J].数理化学习，2018（07）：17-18.

[2]单红利.运用迁移原理促进学生认知[J].中小学数学，2018（04）：17-18.

[3]宋亚东.现代教育技术在小学数学教学中的优缺点分析[J].數学学习与研究，2018（04）：52.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。