黄家豪 郝润科 吕刚震


摘 要:清扫机器人进行全遍历路径规划要求机器人能够遍历环境中所有的可清扫区域,因此提出一种基于蚁群系统算法的地图全遍历路径规划算法。使用搭载单线激光雷达传感器的机器人进行环境建图,对每个栅格赋予不同概率值反映环境状态信息;采用 Boustrophedon细胞分解方法将栅格地图划分为若干相邻子模块,并让机器人从起始点开始遍历所有子模块后再回到起始位姿。为了提高各子模块之间的衔接效率,引入蚁群系统算法实现机器人在到达每个子模块的起始位姿后,对每个子模块进行高效的区域全覆盖。实验结果表明,该算法相比传统生成树算法,清扫覆盖率达到了96%,清扫效率提高了两倍。
关键词:全遍历路径规划;清扫机器人;栅格地图;蚁群系统算法;Boustrophedon细胞分解
DOI:10. 11907/rjdk. 192275 开放科学(资源服务)标识码(OSID):
中图分类号:TP301文献标识码:A 文章编号:1672-7800(2020)007-0041-05
Map Full Traversal Path Planning Based on Ant Colony System Algorithm
Huang Jia-hao, HAO Run-ke, LV Gang-zhen
(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)
Abstract: The full traversal path planning of the cleaning robot requires the robot to traverse all the cleanable areas in the environment. This paper proposes an algorithm for map full traversal path planning based on ant colony system algorithm. The robot is equipped with a single-line lidar sensor for environmental mapping. Each grid gives different probability values to reflect the state information of the environment. The Boustrophedon celluar decomposition method is used to divide the grid map into several adjacent sub-modules. And the robot traverses all submodules from the starting point and then return to their starting pose. In order to improve the connection efficiency between the various sub-modules, an ant colony system algorithm is introduced to realize that after the robot reaches the starting position of each sub-module, it covers the entire area of each sub-module efficiently. The experimental results show that compared with the traditional spanning tree algorithm, the proposed algorithm has a cleaning coverage rate of 96% and the cleaning efficiency is doubled.
Key Words: full traversal path planning; cleaning robot; grid map; ant colony system algorithm; Boustrophedon cell decomposition
0 引言
地圖全遍历路径规划算法旨在解决如何覆盖工作环境中的所有区域并避开障碍物。该算法被广泛应用于各种机器人平台中,例如清洁机器人[1-2]、排雷机器人[3]、割草机器人[4]等。
根据是否有先验的环境信息存储在系统中,全遍历路径规划算法可分为在线方法[5-6]和离线方法[7]两种。在线方法致力于未知环境实时规划与覆盖,但由于传感器自身精度的局限性,存在无法覆盖环境中所有区域的问题。离线方法虽具备更高的覆盖率,并能生成更优路径,但在环境发生变化时极易出现算法失效的情况。Ribeiro 等[8]提出的生成树算法和Hu等[9]提出的螺旋填充路径算法虽然能基本实现地图全遍历路径规划,但因生成的路径重复率太高,导致清扫效率较低;Karthikeyan等[10]提出的基于神经网络算法的路径规划和Yakoubi等[11]提出的基于遗传算法的路径规划虽然能生成优于前者、重复率较低的全遍历路径,但神经网络和遗传算法主要用来解决最短路径优化问题,最短路径优化中的目标函数通常是连续的,并且最终会收敛到特定的最优值,且全遍历路径规划中的最大覆盖范围会对目标函数进行严格约束,若面对多变的复杂环境,机器人也无法保持正常工作状态。
空间分解技术[13]是全遍历路径规划中的关键一环,选择适当的空间分解技术能极大地简化环境模型并降低算法整体复杂度。基于栅格的分解方法[14]将环境空间划分为较小单位元素的并集,其中所有单元的大小与形状相同,且不存在任何重叠区域。同时,每个栅格大小决定了地图分辨率,高分辨率的地图可使算法对工作环境进行更好的估计,达到更高的覆盖率。
故本文通过引入蚁群系统算法[15-16],使用搭载单线激光雷达传感器的清扫机器人构建环境的高分辨率地图,并对地图进行Boustrophedon细胞分解[17],规划出全覆盖的全局路径。该算法相比传统算法具有更高的覆盖率与更低的重复率,弥补了传统算法在动态环境中容易失效的缺陷。
1 基于蚁群系统算法的全遍历路径规划算法
1.1 占用栅格地图构建
栅格地图由Moravec等[18]提出,该方法简单、直观且数据容易表示,所以被广泛应用于机器人避障导航、位姿估计及路径规划等方面,特别适合于处理激光雷达采集的数据。占用栅格地图构建算法可根据给定数据计算整个地图的后验概率。
式中,m为地图,[z1:t]为指导时刻t的所有测量值,[x1:t]为包含所有机器人位姿的路径。
这里采用对数表达形式,以避免0和1附近数值的不稳定性,即:
则式(1)转化为:
因此,将求解整个地图转换成求解每个栅格的概率问题,并将每个单元被占有的概率记为置信度。
当机器人位姿发生改变时,再将当前观测的局部地图融入到已有的全局地图中。图1为单线激光雷达构建的实际环境1的栅格地图,图2为实际环境2的栅格地图。
1.2 环境栅格地图噪声处理
如图1、图2所示,使用单线激光雷达传感器构建的占用栅格地图不可避免地会存在许多噪声点和发散点,并且地图中有许多穿透玻璃门扫到的室外区域,这些区域都不在室内清扫机器人的清扫范围内,所以需要去除栅格地图中的噪声。
本文使用OpenCV中的膨胀与腐蚀算法[19]对栅格地图进行去噪,并确定清扫机器人作业范围。膨胀和腐蚀是图像形态学中的重要操作,原理为对图像进行卷积操作,其需要有一个kernel卷积核,常见的是3*3的矩阵。但与卷积不同的是,如果矩阵中的像素点有任意一个点的值是前景色,則设置中心像素点为前景色。在算法处理前,先将地图变成二值图像,用数值1表示障碍物,数值0表示空闲区域。
采用腐蚀算法,用3*3的kernel扫描图像每一个像素,并用kernel与其覆盖的二值图像作“与”操作,如果都为1,最终图像的该像素为1,否则为0;采用膨胀算法,用3*3的kernel与其覆盖的二值图像作“与”操作,如果都为0,最终图像的该像素为0,否则为1。
图1中的原始栅格地图经过OpenCV中的算法处理后得到如图3所示地图。
1.3 Boustrophedon细胞分解
Boustrophedon细胞分解是一种栅格地图分解方法,算法原理为:切片扫过有界自由空间,从“负无穷大”开始,在切片最初遇到自由空间时生成第一个细胞;然后切片继续扫过自由空间。在IN事件中,切片连通性增加,当前细胞关闭,两个新细胞被打开。相反,在切片连通性降低的OUT事件中,两个当前细胞关闭,一个新细胞被打开。当切片离开有界自由空间时,该过程终止。在计算分解时,还要确定邻接图。同样,每个细胞是图中的节点,并且是边连接的相邻节点。用类似深度优先的图搜索算法输出表示通过邻接图的穷举遍历路径列表,遍历路径列表构成了对邻接图的详尽遍历;最后,使用上述路径列表计算机器人的实际路径。当机器人进入“未清理”单元时,进行Boustrophedon运动,然后计算路径列表中的下一个单元路径。当机器人进入“已清理”单元时,只是计算通过当前单元格到路径列表中下一个单元的路径。重复这两个动作,直到到达路径列表末尾,即直到每个单元都已被“清理”。IN事件和OUT事件分别如图4、图5所示。
在对图3完成Boustrophedon细胞分解后,得到如图6所示分块地图。对实验环境2也进行Boustrophedon细胞分解,得到如图7所示分块地图。
1.4 蚁群系统算法
将环境栅格地图分解为多个子区域后,需要给清扫机器人规划出一条从起点开始访问所有子区域,最后又回到起点的最优路径,也即组合优化问题中的旅行商问题。该问题是在一个带权完全无向图中寻找一个权值最小的Hamilton回路[20]。由于该问题的可行解是所有顶点全排列,随着顶点数的增加,会产生组合爆炸,因此是一个NP完全问题。图8是实验环境1的区域结构图,根据该图直接实现全遍历规划算法是不现实的。
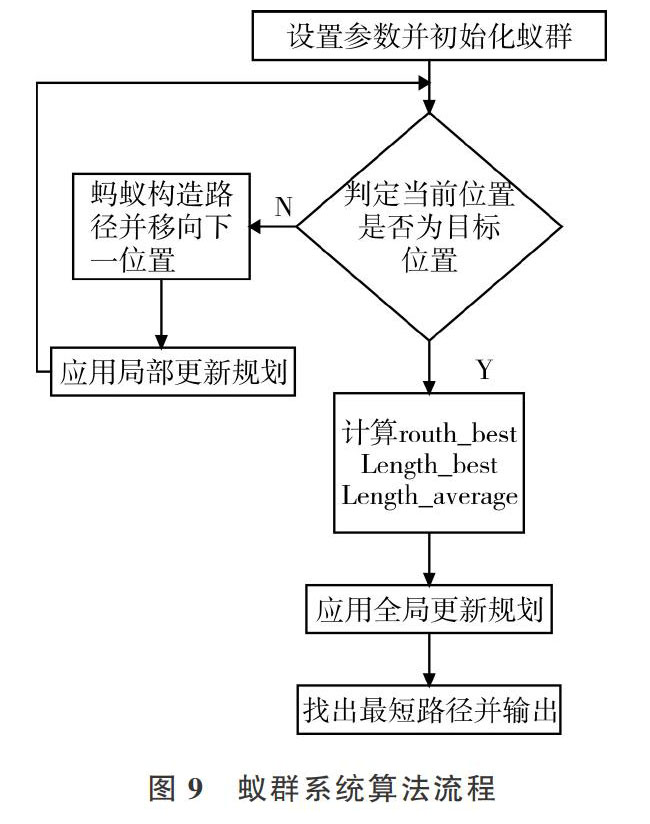
蚁群系统算法(Ant Colony System,ACS)是一种基于群体、用于求解复杂优化问题的元启发式算法。与真实蚂蚁通过外激素的留存、跟随行为进行间接通信类似,ACS中一群简单的人工蚂蚁之间通过媒介质进行间接通信,并利用该信息以及与问题相关的启发式信息逐步构造问题的解,实现对问题的优化。算法流程如图9所示。
根据图8得到一个有向图G的三元组为(V,E,f),其中V是一个非空集合,其元素称为有向图节点;E是一个集合,其元素称为有向图的边;f是从E到V×V的一个映射。E中元素总是与V中的序偶有对应关系,可用V中的序偶代替E中元素,则G简记为(V,E)。
设[C=c1,c2,?cn]为n个城市的集合,[L=lij|ci,cj∈C]是集合C中元素两两连接的集合,[diji,j=1,2,?,n]是[lij]的Euclidean距离,如式(6)所示。
G=(C,L)构成一个有向图,从G中寻找长度最短的Hamilton圈,即全遍历路径。
在蚁群系统算法中,蚂蚁采用伪随机比例规则策略。根据该策略,一只位于子区域1的蚂蚁k通过公式(5)选择下一个要访问的区域j。
q为[0,1]区间均匀分布的随机数,[q0]为一个参数,[0q01]。蚂蚁k以[q
- 旅游宣传与现代手段的碰撞
- 以科技创新推动全域旅游发展的研究
- 大连市会展旅游研究综述
- 冬奥会背景下虚拟现实技术对冰雪体育旅游目的地营销效果的影响研究
- 开平碉楼旅游业融资机制研究
- 全域旅游视角下绍兴红色旅游的创新发展研究
- 阿尔山市冰雪旅游游客满意度影响因素研究
- “互联网+”背景下益阳竹艺旅游资源与现代元素结合的商品化开发分析
- 基于大学生群体的沈阳市“微旅游”产品创新研究
- 循环经济思想在绿色饭店建设中的实践研究
- 基于网络游记的重庆旅游形象感知与推广研究
- 生态文明建设背景下常德市研学旅行课程开发研究
- 文旅融合背景下苏州博物馆文创产品的营销策略研究
- 文旅融合背景下湛江海洋文化遗产活化利用研究
- 辽西锦陶饰品产业化发展的SWOT分析
- 徐霞客与贵州旅游资源开发
- 论瑶语的保护和传承
- 非物质文化遗产的传承与发展研究
- 智慧旅游发展对策研究
- 寓教于乐的田园亲子游公共空间设计策略
- 基于大健康产业背景下广西老年旅游发展对策研究
- 崇州市融入成都世界旅游目的地建设路径探究
- 新疆生产建设兵团红色旅游发展研究
- 跨境电商视域下乡村旅游的困境与出路
- 试析休闲农业与乡村旅游创新发展策略
- communally
- commune
- communed
- communer
- communers
- communer's
- communes
- communes'
- commune²
- commune¹
- communicate
- communicated
- communicatees
- communicates
- communicating
- communication
- communicational
- communicationally
- communications
- communicative
- communicatively
- beat sb up
- beat sb ↔ up
- beats me
- be-at-someone
- 臣子向皇帝陈述事状
- 臣子因进谏触犯皇帝而获罪
- 臣子在君王前的自称
- 臣子夺取君位
- 臣子对他国谦称自己的国君
- 臣子对帝王陈述意见或说明事情
- 臣子总是按照君主意图行事
- 臣子或仆人忠于君主或主人
- 臣子朝拜皇帝的地方
- 臣子朝见君主
- 臣子的权力大于国君
- 臣子的灵柩葬在皇帝坟墓的旁边
- 臣子盗取君位
- 臣子篡夺君位
- 臣子获得君王的信任
- 臣宪
- 臣宰
- 臣对君卑称自己的年龄
- 臣对君的谦称
- 臣属依附
- 臣属向皇帝上书的名称之一
- 臣属当面回答皇帝提出的问题
- 臣工
- 臣心似水
- 臣心如水