《高阶时滞系统辨识方法》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

高阶时滞系统辨识方法

范文

李海龙王亚刚

摘要：工业生产中高阶系统较为复杂，为了改善系统辨识效果和模型预测控制，在二阶加时滞系统基础上进行改进。运用频域方法，对高阶时滞系统进行研究。在系统低频和中频段找出合适的采样区间。对系统划分子区间长度，对输出信号进行拟合，使系统进行数次迭代，求出临界频率，确定高阶系统的重要频率段，得出辨识系统在频率段的特性响应矩阵。通过幅值和相位关系，采用最小二乘法拟合二阶加滞后模型参数。利用MATLAB对模型进行验证，得出系统的Nyquist曲线和单位阶跃响应曲线。仿真实验表明，辨识的系统结构简单，有利于系统的整体控制和控制器参数整定，整个系统辨识效果提高了[31.65%]，达到了对系统降阶的目的。

关键词：模型辨识;二阶加纯滞后模型;最小二乘法;频率响应;MATLAB仿真

DOI：10. 11907/rjdk. 192599 开放科学（资源服务）标识码（OSID）：

中图分类号：TP301文献标识码：A 文章编号：1672-7800（2020）007-0066-04

Identification Method for High Order Time Delay Systems

LI Hai-long，WANG Ya-gang

（School of Optical-Electrical and Computer Engineering，

University of Shanghai for Science and Technology，Shanghai 200093， China）

Abstract： In industrial production， higher-order systems are more complicated. In order to improve system identification effects and model predictive control， improvements are made on the basis of second-order time-delay systems. In this paper， the frequency domain method is used to study high-order time-delay systems. This study finds suitable sampling intervals in the low-frequency and mid-frequency bands of the system， divides the sub-interval length of the system， fits the output signal， makes the system iterate several times， finds the critical frequency， and determines the important frequency band of the higher-order system. The characteristic response matrix of the identification system in the frequency band is obtained. Through the relationship between amplitude and phase， the least square method is used to fit the parameters of the second-order plus lag model. By using MATLAB to verify the model， the system Nyquist curve and unit step response curve are obtained. Simulation experiments show that the identification system has a simple structure， which is conducive to the overall control of the system and the setting of controller parameters. The identification effect of the entire system is improved， and the purpose of order reduction is achieved.

Key Words： modeling identification; second order with pure time delay model; least square method; frequency response; MATLAB simulation

0 引言

系統辨识是在未知系统模型情况下，在典型激励信号输入后获得输出响应，根据输出响应和输入信号，预测系统的传递函数模型[1]。工业受控对象大多是非线性、多容、高阶的，常用的辨识方法有多层递阶法、面积法、模糊逻辑法、小波网络法、连分式法等[2-6]。Ahmed&Shah等 [7]提出基于阶跃响应的系统辨识方法，但算法比较复杂且只能辨识滞后环节较小的对象;李大字等[8]提出了基于阶跃响应和开闭环转换的三步法辨识，但不能准确辨识纯滞后的系统阶次;闫子豪等[9]利用继电反馈，将积分系统组合进行参数辨识和整定，利用相角偏移补偿继电反馈振荡点与临界值之间的误差。但系统需要多个组合积分器，辨识模型需要利用多个积分环节;陈安钢等[10]对模型进行降阶，使用PI（D）对系统进行辨识，但在实际模型中对系统降阶处理会导致系统振荡环节减少，出现一定误差。针对工业带有时滞环节的高阶系统，采用对二阶系统模型参数进行改进的方法，利用得出的重要频率段，在频率段内对系统进行拟合，利用幅频关系辨识系统模型。

工业上一般都采用MATLAB自带的系统辨识工具箱辨识一阶加时滞环节和二阶加时滞环节[11]，通过最小二乘法对系统对象进行辨识。本文在二阶加时滞系统改进模型参数，通过频率段特性响应矩阵，在系统重要频率段中选择适当的频率点个数，拟合出二阶加滞后模型[12]。

1 高阶时滞对象频率特性

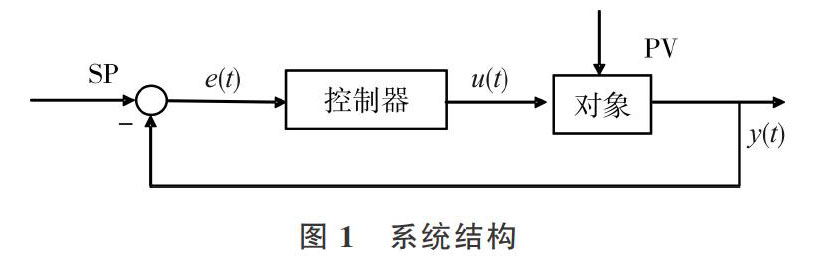
在工业系统控制中被控对象在控制器的控制下，在外部输入激励信号[u（t）]，经过系统内部相互作用，测得系统实际输出，通过高阶模型近似逼近出闭环模块的传递函数，对系统进行建模分析，得出辨识结果。外部输入均为多输入多输出的非线性高阶系统，SP是多输入系统的设定目标值，[u（t）]为系统输入激励信号，[y（t）]为系统实际输出信号，系统结构如图1所示。

其中，SP为设定的目标值;PV为动态值，即实际测量值;[e（t）]为扰动信号。

激励信号[u（t）]的动态信号中包含激励信号的频域信息，但其不一定可积[13]，对信号[f（t）]作处理，将其分为稳态信号[Δf（t）]和瞬态信号[fs（t）]。

进行[Laplace]变换得：

若系统输出信号在[t=T]时刻达到稳定状态，此时瞬态响应[fs（t）]的值为0，由式（2）可得：

系统在[t=T]时刻，模型的输入信号和输出响应由式（3）得出当前时刻的传递函数模型：

将阶跃信号作为系统的输入时，[Δu（t）=0]，输出则为瞬态响应和稳态响应。令[s=jω]，得式（5）[14]。

式（5）在采样时间[ti] 到[ti+1]时间内，对系统输出响应进行拟合，将输出响应划分为M长度[Δli] 的子区间。

通过式（6）可确定系统的重要频率段。任意给定频率[ω]，都可根据式（6）求出频率[ω]的幅值和相位参数。

1.1 高阶时滞对象频率特性

若模型收敛则系统主要受影响部分为低频段和中频段，系统高频段受到的影响较小，所以采用从零开始直到找出相角由正变负的起始频率作为系统的频率范围，临界频率作为终点频率，进行迭代得[15] ：

经过数次迭代即可求出临界频率点[ωc]，则[（0，ωc）]为重要频率段[16-17]。

2 高阶时滞对象传递函数模型

根据式（7）求得频率段，可以得到其频率特性，在频率段内选取[M]个频率点，采用改进二阶加滞后模型辨识方法，其传递函数模型如下：

3 仿真实验

为评估模型的准确性，仿真实验使用高阶振荡模型和高阶非振荡模型[19-20]，使得辨识模型更加具有普适性。

采用本文使用的辨识方法，系统的主要频率段为[0，0.123 5]，令M=15，主要频率段选取15个频率点，最终辨识模型为：

初始系统和辨识系统的Nyquist如图2所示。

初始系统和辨识系统的单位阶跃响应如图3所示。

假设高阶非振荡系统模型为：

采用本文使用的辨识方法，系统的主要频率段为[0，0.171 5]，令M=15，主要频率段选取15个频率点，最终辨识的模型为：

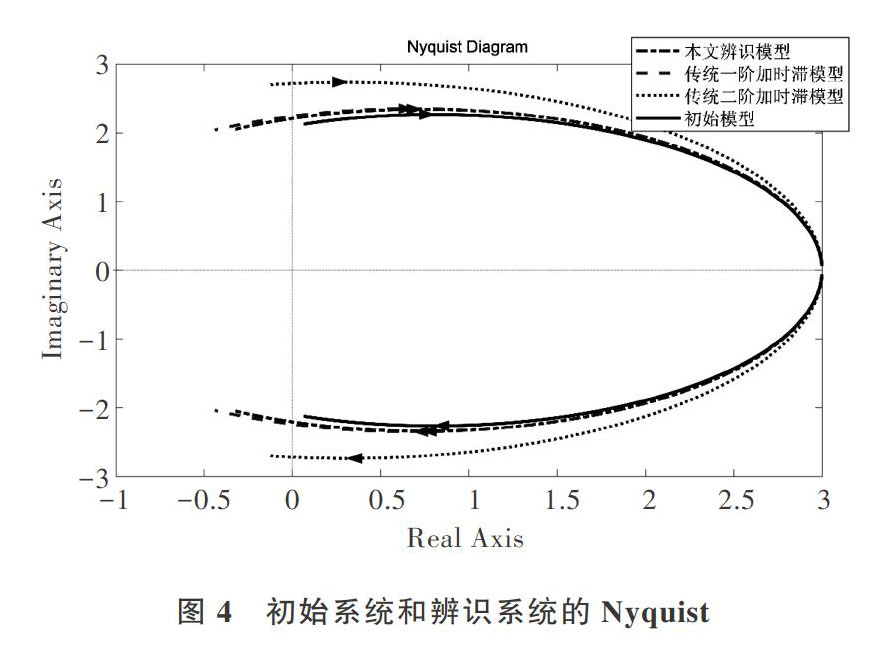
初始系统和辨识系统的Nyquist图如图4所示。

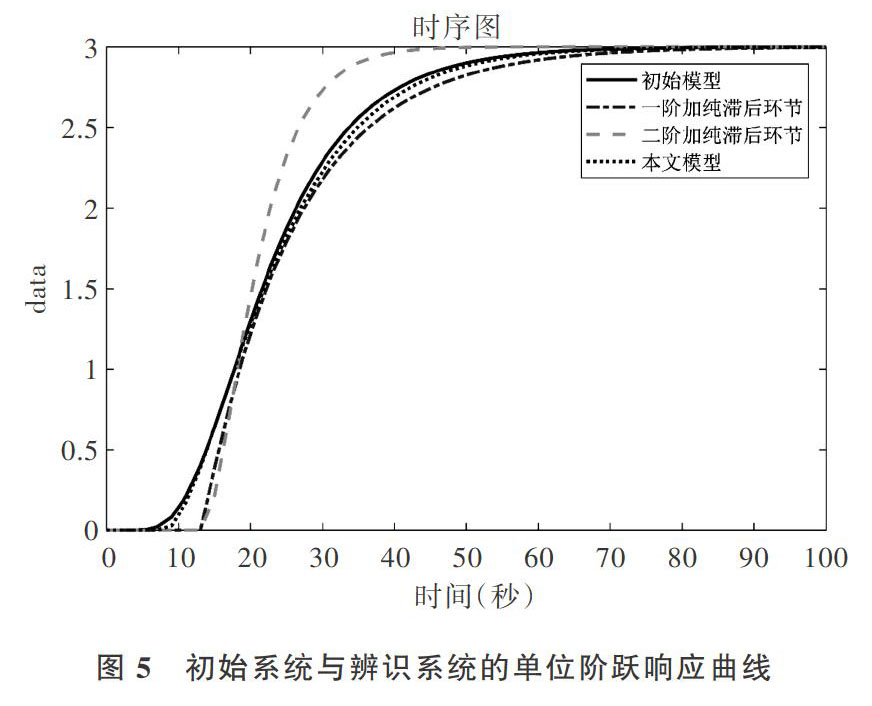
初始系统和辨识系统的单位阶跃响应如图5所示。

由图（2）-图（5）的仿真实验结果可以看出，MATLAB中自带的系统辨识工具箱辨识的一阶和二阶模型，和初始模型相比都有一定的误差，在低频段和中频段对初始模型能准确拟合响应信号，对高阶系统的辨识效果提高了31.65%。利用输出信号划分的M个区间，确定频率范围，消除噪声影响。结合最小二乘法对M区间内的频率进行拟合以确定最终的模型参数T1、T2、L、K。通过上述分析，文中采用的方法具有较高的稳定性和精确性。

4 结语

本文对高阶时滞对象辨识进行改进，对辨识对象子区间进行划分，获取频率范围，选择重要频率段内的15个频率点，对选择的频率点进行迭代。通过特性响应矩阵求出辨识模型参数，使得高阶时滞系统可以更好地应用于工业生产中。通过仿真实验对辨识系统加入单位阶跃信号，获取系统输出。本文可对参数模型进行改进，增加频率点个数，以进一步提高准确性。本文没有对噪声或者干扰进行辨识仿真，后续可以在系统中增加频率点、加入扰动进行辨识。

參考文献：

[1] 王维贺，王平. 二阶加纯滞后对象模型辨识方法及其应用[J].? 化工自动化及仪表，2010， 37（9）： 21-24.

[2] 姜永明，王长青，徐骋.? 基于递推最小二乘法的飞行器模型参数在线辨识[J].? 控制与信息技术，2019（4）： 58-64.

[3] 李闯，王亚刚. 对高阶对象的一种模型辨识方法[J]. 软件导刊，2019（1）：174-177.

[4] 顾玮. 基于最小二乘法的系统参数辨识[J]. 科研教育，2017（263）：39-41.

[5] 李少远，蔡文剑. 工业过程辨识与控制[M]. 北京：化学工业出版社，2005.

[6] 萧德云. 系统辨识理论及应用[M]. 北京：清华大学出版社，2014.

[7] AHMED SALIM，HUANG BIAO，SHAH S L. Novel identification method from step response[J]. Control Engineering Practice，2017 （15）：545-556.

[8] 李大字，曾繁友，靳其兵，等. 基于阶跃响应和开闭环转换的三步法辨识[J]. 仪器仪表学报，2009，30（6）：30-33.

[9] 闫子豪，任正云，陈安钢. 基于继电反馈的组合积分系统参数辨识与整定[J]. 石油化工自动化，2017，53（5）：33-38.

[10] 陈安钢，任正云，倪潇. 复杂高阶对象的预测PI（D）控制[J]. 计算机测量与控制，2017，25（6）：37-40.

[11] 李晓枫，陈广学. 采用基于闭环辨识IMC-PID实现串级汽温的鲁棒控制[J]. 中国电力，2017，50（11）：15-21.

[12] 单永明，王亚刚，王凯. 高阶加时滞模型的系统频域辨识[J]. 电子科技，2019，23（3）：6-9.

[13] 王贤平，王亚刚，李晓枫，等. 含微分环节过程对象模型的频域辨识方法[J]. 控制工程，2015，22（5）：1006-1009.

[14] 王亚刚，许晓鸣. 复杂多变量过程模型的闭环频域辨识[J]. 控制与决策，2010，25（6）：825-830.

[15] MI? W T，QIAN S，LI S. Basis pursuit for frequency-domain identification[J]. Mathematical Methods in the Applied Sciences，2016，39（3）：498-507.

[16] 胡钢墩，李发泽. 惯性系统的时域在线辨识[J]. 控制与决策，2010，25（1）：133-136.

[17] 谭功全，干树川，陈永会. 一阶时滞过程PID控制器优化准则[J]. 控制工程，2012，19（5）：798-801.

[18] 冯利卿. 含有混合噪声的线性系统的频域辨识[D]. 成都：电子科技大学，2018.

[19] 侯媛彬，汪梅，王立琦. 系统辨识及其Matlab仿真[M]. 北京：科学出版社，2004.

[20] 吕秋霞，李继容.? Matlab在系统辨识中的应用[J]. 仪器仪表用户，2008，15（1）：60-61.

（责任编辑：杜能钢）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。