《一种新颖的数字图像篡改检测方法》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

一种新颖的数字图像篡改检测方法

范文

王泓鑫李硕

摘要：检测数字图像复制—粘贴型篡改是目前研究热点之一。多数复制—粘贴篡改检测方案只对刚性平移篡改具有较好的检测精度，无法有效应对更复杂的几何变换和常规信号攻击。为优化数字图像复制—粘贴篡改检测效率和精度，首次提出一种使用极坐标复指数变换（PCET）与一致性敏感哈希（CSH）的高效检测算法。首先，计算滑动窗口PCET系数，将其作为不变的图像局部特征;然后，根据这些特征，利用CSH算法快速、精确地匹配大量密集分块;最后，使用基于密集线性滤波的后处理算法消除匹配结果中的错误匹配并定位重复区域，得到最终检测结果。根据实验结果可知，该算法不仅检测精度平均提高12.06%，而且处理时间平均缩短315.64s。因此利用对几何变换和常规信号攻击鲁棒的PCET系数刻画图像局部特征，并采用基于图像一致性的快速高精度匹配算法CSH，可有效优化复制—粘贴篡改检测精度和效率。

关键词：复制—粘贴型篡改;图像矩;区域复制;旋转不变

DOI：10. 11907/rjdk. 192614 开放科学（资源服务）标识码（OSID）：

中图分类号：TP317.4 文献标识码：A 文章编号：1672-7800（2020）008-0221-05

Abstract： Detecting copy-move forgery of digital images is one of the current research hotspots. However， most existing copy-move forgery detection schemes are generally only robust to translation， and they are not effective in dealing with more complex geometric transformations and conventional signal processing attacks. In addition， such algorithms are often time-consuming and cannot meet the needs of real-time detection. In order to optimize the efficiency and accuracy of digital image copy-move forgery detection， a fast and effective algorithm using polar complex exponential transform （PCET） and coherency sensitive hashing （CSH） was proposed in this paper. First， the algorithm calculates the PCET coefficients of the sliding windows as invariant local features. Then， based on these feature vectors， a large number of dense windows will be quickly and accurately matched by the CSH algorithm. Finally， the dense linear fitting （DLF） based post-processing algorithm is used to eliminate the mismatches and locate the duplicated regions. In this paper， five challenging tampered images are selected from GRIP and FAU databases， and the accuracy and speed are compared with classic algorithm. According to the experimental results， the proposed algorithm not only improves the average detection accuracy by 12.06%， but also reduces the average processing time by 315.64 seconds. PCET coefficients that are robust to geometric transformations and conventional signal processing attacks are used to characterize image local features. Moreover， image coherency based CSH is introduced for fast and high-precision feature matching. Therefore， the proposed algorithm is able to effectively optimize the accuracy and efficiency of detection.

Key Words： copy-move forgery;image moment; region duplication; rotation invariance

0 引言

圖像作为人类最重要的信息来源之一，在群体和个人意见形成过程中扮演关键角色。然而，现代图像处理软件（Photoshop、Gim）及个人电脑和终端的快速推广，使人们可以极低的成本篡改数字图像内容。这对数字图像可靠性产生了严重威胁，若篡改的图像应用于关键场景，可能导致严重的社会后果。

复制—粘贴篡改是一类常见的图像篡改手段，其中图像一个或多个区域被复制并粘贴在同一图像中的其它位置，其目的是隐藏或强调感兴趣的对象[1]。尽管该篡改过程非常简单，但由于图像存在同源性和差异性，检测难度较大。在过去的10年中，多个复制—粘贴篡改检测方案被提出[2- 3]。它们基本遵循一个通用框架：特征提取、特征匹配和后处理。根据是从每个像素中提取局部图像特征，还是仅从某些选定特征点中提取特征，检测方案可分为两大类：基于块的方法和基于特征点的方法。其中，基于特征点的方法因为特征点稀疏性，检测结果通常不如基于块的方法精确。对基于块的方法，现有文献更多关注特征提取和匹配两个阶段。

在特征提取方面，不同的篡改检测方法使用不同的变换描述图像块。常用变换方法包括离散余弦变换（Discrete Cosine Transform，DCT）[4]、离散小波变换（Discrete Wavelet Transform，DWT）[5]、傅立叶变换（Fourier Transform，FT）[6]、主成分分析（Principal Component Analysis，PCA）[7]和奇异值分解（Singular Value Decomposition，SVD）[8]。但是，这些特征在旋转和缩放攻击下非常脆弱。因此，出现新算法使用更复杂的几何不变变换，如Hu矩（Hu Moments）[9]、泽尼克矩（Zernike Moments，ZM）[10]、傅里叶—梅林变换（Fourier-Mellin Transform，FMT）[11]和极坐标余弦变换（Polar Cosine Transform，PCT）[12]。这些方法在抵抗几何攻击方面表现出更出色的检测精度。

在特征匹配方面，大量图像块（105～106）需进行匹配以揭示篡改。传统匹配算法主要包括暴力搜索、字典排序、KD树和局部敏感哈希算法（Locality Sensitivity Hashing，LSH）[13]，通常需高昂的时间成本。这主要是因为这些技术是通用的，并非专门用于篡改检测任务，还忽略了该领域一项重要的先验知识：自然图像平滑性和自相似性意味着领近像素最近邻在空间上很大可能也彼此接近。受此启发，一些更适用于复制-粘贴篡改检测的匹配算法受到关注，包括PatchMatch [14]和一致性敏感哈希算法（Coherency Sensitive Hashing， CSH）[15]。由于充分利用了先验知识，这些对特征点位置敏感的新颖匹配策略在时间效率方面大幅度领先于其它方法。

为优化数字图像复制—粘贴篡改检测效率和精度，本文首次提出一种使用极坐标复指数变换（PCET）[16]与一致性敏感哈希（CSH）[17]的高效检测算法。首先，计算滑动窗口PCET系数，并将其作为不变的图像局部特征;然后，根据这些特征，大量密集分块由CSH算法快速、精确地匹配;最后，使用密集线性滤波（Dense Linear Fitting，DLF）[14]处理算法消除匹配结果中的错误匹配，并定位重复区域，得到最终检测结果。根据实验结果可知，该算法不仅可大幅提高检测精度，还可极大压缩基于块的检测算法时间成本。

1 复制—粘贴篡改检测算法

1.1 极坐标复指数变换

极谐变换（Polar Harmonic Transforms，PHTs）由Yap等[16]于2010年提出，是一种定义域为单位圆的新型正交矩。PHTs包括极坐标复指数变换（PCET）、极坐标余弦变换（PCT）和极坐标正弦变换（Polar Sine Transform， PST）。本文聚焦于PCET。

由式（7）可知，将图像旋转一个角度后的PCET的模与原始图像PCET的模相等。

1.2 一致性敏感哈希算法

一致性敏感哈希（CSH）算法 [17]扩展于LSH算法和PatchMatch算法，可达到快速匹配图像片段的效果。LSH基于图像哈希算法，它会将相似的图像块投影到相同的桶（Bin）中，因此算法可在桶中找到匹配圖像块。LSH匹配精度虽然很高，但需高昂的计算成本。PatchMatch算法则基于图像一致性，在自然图像中迭代地进行最优偏移向量估计，并利用一致性获得全局最优的匹配偏移。由于使用了先验知识，算法计算复杂度很低，但有随机性和匹配误差大等缺点。CSH是LSH和PatchMatch的融合算法，首先CSH使用LSH查找初始匹配图像块（而不是使用PatchMatch的随机初始化），然后再利用PatchMatch在图像中具有一致性的区域拓展正确匹配（而不是仅使用CSH的图像哈希）。通常，CSH匹配时间远少于PatchMatch，且匹配精确也更高。显然CSH对于自然图像篡改检测任务非常有效。

CSH算法流程可分为两大部分：建立索引和搜索。算法输入是特征矩阵[A]和[B] （[A]和[B]可以相同），[A]为源，[B]为目标，输出是近似的最近邻域（Approximate Nearest Neighbor Fields，ANNF）。

1.2.1 索引建立

如此操作直至穷尽[PB]中的所有元素。

在上述搜索流程中，生成最近邻候选集[PB]是关键操作。为简化讨论，首先引入几个标记。定义哈希函数为[g]，由该函数生成的哈希表为[T]。此外，将哈希函数[g]分为[gA]和[gB]：当对[A（B）]中的块[a（b）]进行哈希时，哈希函数[g]标记为[gA（gB）]，生成的哈希表记为[TA（TB）]，并引入[gA]（[gB]）的逆运算[g-1A]（[g-1B]）。块[p]的上、下、左、右邻接块分别记[Top（p），Bottom（p），Left（p），Right（p）]。[A]中的块[a]在[B]中目前已知的最近邻块记为[Cand（a）]。

CSH算法匹配候选技术基于以下4个定理，其中，[a，a1，a2]是[A]中的块，[b，b1，b2]是[B]中的块。

定理1：如果[gA（a）=gB（b）]，则[b]是[a]的一个（最佳）候选。

定理2：如果[b]是[a1]的候选，并且[gA（a1）=gA（a2）]，则[b]也是[a2]的候选。

定理3：如果[b1]是[a]的候选，并且[gB（b1）=gB（b2）]，则[b2]也是[a]的候选。

定理4：如果[b]是[Left（a）]的候选，则[Right（b）]是[a]的候选（该定理对于Right/Left Top/Bottom和Bottom/Top对同样成立）。

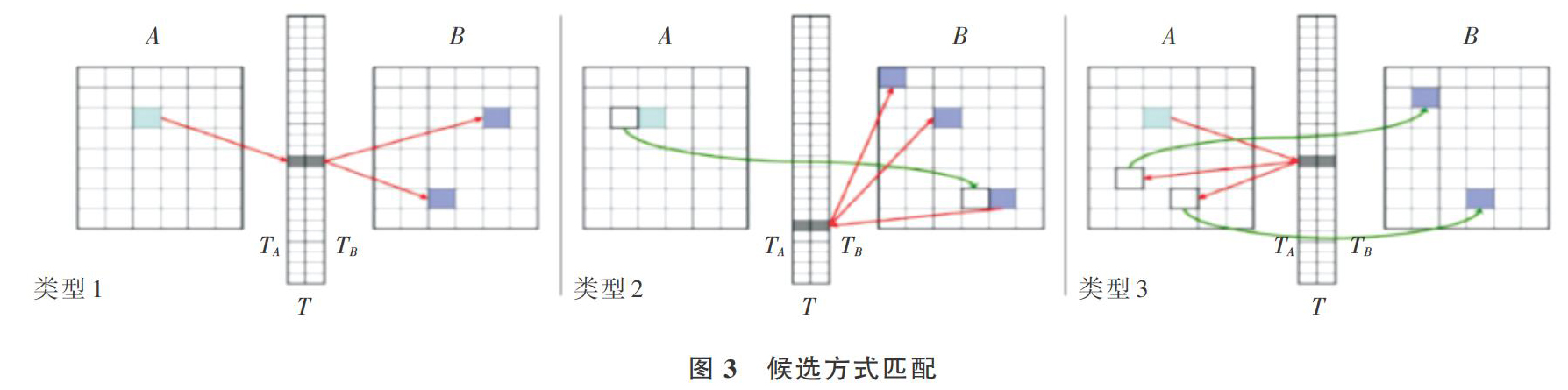
上述4项定理出自LSH和PatchMatch算法假设，其中定理1至定理3源自LSH，依赖于表示空间，定理4出自PatchMatch，依赖于一致性。以这4条定理为基础，CSH算法定义了3种匹配候选方式，其公式定义和直观表示分别见表1、图3（彩图扫描OSID码可见），该定义对于类型2，Top/Bottom对同样成立。

图3中，红色箭头表示哈希函数[g]（请注意箭头方向和表1公式定义之间的对应关系），绿色箭头表示目前已知最近邻块[Cand（）]，[A]中的浅蓝色块表示[a]，[B]中紫色块并集是[a]的最近邻候选集[PB]，在[A]和[B]中间的哈希表[T]实际上是由[TA]和[TB]合并得到的，[TA（TB）]的宽度指哈希表中每个桶最多可储存的块数，设置为[k]。则在理想情况下，类型1和类型3每个类型将贡献[k]个候选块，类型2中Left/Right对和Top/Bottom对每对将贡献[k+1]个候选块，因此[PB]的势最大为[4k+2]。

可以看出，CSH的3种匹配候选方式融合折中了LSH与PatchMatch的匹配方式，这使得CSH算法高效且精确。通过3种匹配候选方式，[A]中的任意块[a]都得到了自己最近邻候选集[PB]。

1.3 算法流程

本文提出的复制-粘贴篡改检测算法充分利用了PCET与CSH的优势。首先，密集图像分块特征表示基于PCET系数，特征对于旋转攻击不变，而且在噪声鲁棒性方面表现良好。这是传统空域特征和频域特征所不具有的。随后，CSH被用于图像密集域局部不变特征的匹配，较于经典的匹配策略，它在特征匹配速度和精度两方面均有大幅改进。整体上算法包括以下步骤：

步骤1：将给定的彩图原始图像变换为灰度图像。

步骤2：计算密集分块的PCET系数 [16]，并取系数的模作为特征。

步骤3：使用CSH [17]对图像块特征进行快速精确匹配，得到相应匹配结果。

步骤4：对匹配结果使用DLF算法[14]进行误匹配筛除，并使用形态学方法优化结果，最后标记篡改区域。

2 实验结果

本文实验环境为：Matlab R2016a、3.60GHz 中央处理器和16GB 内存。为使实验结果更有说服力，来自GRIP [14]和FAU [18]数据库的5幅测试图像用于本次实验。

算法參数方面，图像块大小为[25×25]、特征的最大阶数为5、匹配对最小距离为50像素、篡改区域最小尺寸为图像尺寸的0.002%。

图4给出了相关实验结果，其中第一列是原始图像、第二列是篡改图像、第三列是真实篡改区域、第四列是文献[19]的检测结果、第五列是本文算法的检测结果。可以看到，本文算法检测精度非常高，对各类篡改（特别是多对象篡改）有很强的检测能力。

3 结语

本文提出了一种新颖的数字图像复制—粘贴篡改检测方法，可同时提高检测精度和效率。该算法充分利用了PCET和CSH技术优势。首先，使用PCET抽取密集图像分块的高阶特征，PCET系数对旋转具有不变性，而且低阶系数对噪声类图像攻击具有鲁棒性。相比于传统空域特征和频域特征，这有助于跨越语义鸿沟;随后，基于图像一致性这一关键先验知识，采用CSH匹配图像密集域局部不变特征。较于计算机视觉领域中常规的匹配策略，CSH在特征匹配速度和精度两方面均具有优势。从具体实验结果来看，本文算法不仅在检测精度上平均高出经典方案12.06%，而且在计算时间方面也比经典方案减少了315.64秒。这证明本文算法具有较好的精度和效率，图像矩方法与基于一致性的匹配算法在复制-粘贴篡改检测领域具有独特优势。

尽管本文算法对于常见的几何攻击（如旋转、缩放、翻转）具有较好的鲁棒性，但由于使用了固定尺寸的图像块，导致缩放鲁棒性仅在有限范围内可满足。下一步将联合尺度空间理论和图像矩方法，寻找一种可行的优化方法。

参考文献：

[1] 吕颖达，申铉京，陈海鹏. 具有几何不变性的图像复制—粘贴盲鉴别算法[J]. 电子学报，2016， 44（11）： 2592-2599.

[2] 毕秀丽，魏杨，肖斌，等. 基于级联卷积神经网络的图像篡改检测算法[J]. 电子与信息学报， 2019， 41： 1-8.

[3] 许曼曼，杨继翔. 数字图像复制—粘贴篡改检测与定位算法[J]. 软件导刊，2016，15（11）： 199-201.

[4] FRIDRICH A J，SOUKAL B D， LUKá ?A J. Detection of copy-move forgery in digital images[C]. Proceedings of Digital Forensic Research Workshop，2003： 94-100 .

[5] MUHAMMAD G，HUSSAIN M，BEBIS G. Passive copy move image forgery detection using undecimated dyadic wavelet transform[J]. Digital Investigation， 2012， 9（1）： 49-57.

[6] BRAVO-SOLORIO S，NANDI A K. Exposing duplicated regions affected by reflection， rotation and scaling[C]. 2011 IEEE International Conference on Acoustics，Speech and Signal Processing，2011： 1880-1883.

[7] POPESCU A C， FARID H. Exposing digital forgeries by detecting duplicated image regions[R]. Dartmouth College： TR2004-515， 2004： 1-11.

[8] ZHAO J， GUO J. Passive forensics for copy-move image forgery using a method based on DCT and SVD[J]. Forensic Science International， 2013， 233（1-3）：158-166.

[9] 王俊文，刘光杰，张湛，等. 图像区域复制篡改快速鲁棒取证[J]. 自动化学报， 2009， 35（12）： 1488-1495.

[10] RYU S J，LEE M J， LEE H K. Detection of copy-rotate-move forgery using Zernike moments[C]. International Workshop on Information Hiding， 2010： 51-65.

[11] BAYRAM S，SENCAR H T，MEMON N. An efficient and robust method for detecting copy-move forgery[C]. 2009 IEEE International Conference on Acoustics， Speech and Signal Processing， 2009： 1053-1056.

[12] LI Y. Image copy-move forgery detection based on polar cosine transform and approximate nearest neighbor searching[J]. Forensic Science International， 2013， 224（1-3）： 59-67.

[13] PUN C M， CHUNG J L. A two-stage localization for copy-move forgery detection[J]. Information Sciences， 2018， 463： 33-55.

[14] COZZOLINO D，POGGI G，VERDOLIVA L. Efficient dense-field copy–move forgery detection[J]. IEEE Transactions on Information Forensics and Security， 2015，10（11）： 2284-2297.

[15] BI X， PUN C M. Fast copy-move forgery detection using local bidirectional coherency error refinement[J]. Pattern Recognition， 2018， 81： 161-175.

[16] YAP P T，JIANG X，KOT A C. Two-dimensional polar harmonic transforms for invariant image representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，32（7）： 1259-1270.

[17] KORMAN S，AVIDAN S. Coherency sensitive hashing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2015， 38（6）： 1099-1112.

[18] CHRISTLEIN V， RIESS C， JORDAN J， et al. An evaluation of popular copy-move forgery detection approaches[J]. IEEE Transactions on Information Forensics and Security， 2012， 7（6）： 1841-1854.

[19] ZANDI M， MAHMOUDI-AZNAVEH A， TALEBPOUR A. Iterative copy-move forgery detection based on a new interest point detector[J]. IEEE Transactions on Information Forensics and Security， 2016， 11（11）： 2499-2512.

（責任编辑：江艳）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。