《计算动词元胞网络中的菱形对称波模式》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

计算动词元胞网络中的菱形对称波模式

范文

李彬　李琳　杨涛

摘要：计算动词元胞网络（CVCN）是一种使用计算动词局域规则的新型元胞计算平台。对于利用语言描述的高级模型来建模人类个体之间的确定与不确定性社会行为，计算动词元胞网络是非常成功的模型。由于计算动词理论有丰富的动词规则，因而计算动词元胞网络有多种形式。元胞网络是建模复杂系统的良好载体，将计算动词应用于元胞网络的构建，是解决复杂社会行为可计算化的一个行之有效的方法。计算动词元胞网络把物理语言学植入到元胞网络的局域规则中，从而实现物理信号推理到符号推理的转变。因此只需简单的计算动词局域规则即可建模高级的社会行为。

关键词：计算动词元胞网络；动词规则；局域规则；菱形对称波模式

中图分类号：TP3-05

文献标识码：A

0 引言

计算动词元胞网络最早由杨涛教授在美国加州大学伯克利分校提出，详细阐述了计算动词元胞网络的结构及一致的规则。元胞网络经由局域规则来维持个体间的联系，这些个体被定义为元胞，元胞间直接联系的范围为每个元胞的局域规则所对应的邻域范围，元胞网络的模式即为输出的结果。而实际上每个元胞只按照各自的局域规则改变，只受其邻域范围内的元胞直接影响，对于邻域外的元胞是由相邻的邻域不断传递来形成间接影响。因而局域规则是维持整个元胞网络动态演化的关键。这与人类的社会行为类似，人类个体只会受到有关联的个体们的直接影响，在其邻域外的个体只能通过元胞间的邻域作用的传递而产生间接影响。

计算动词元胞网络结构与元胞自动机结构相似，中间细胞的状态会被周围细胞在每次细胞迭代中影响。然而，它们又存在一些不同点，元胞自动机的状态是有限的，它们非0即1；而计算动词元胞网络是基于计算动词理论并且考虑过程及细胞状态的变化。举例来说，用“increase”来表达细胞现在的状态比上一个状态更大，定义标准计算动词为{increase，stay，decrease}，利用细胞动词状态值之间的相似性和标准动词来定义细胞状态值变化程度的权重。在计算动词元胞网络中，细胞连续性的状态值即计算动词元胞网络的模式比元胞自动机的模式要丰富得多。

元胞自动机被广泛地应用在物理、生物及社会关系的模型中。目前，我们需要从不同方式来对物理场景进行建模。计算动词元胞网络通过将动力学系统引入到局域规则的结构中去而产生了元胞自动机。在论文中研究了一维计算动词元胞网络。在论文中讨论了三种一维计算动词元胞网络模式，分别为同质模式，棋盘模式和翻转模式。在论文中呈现出来一维计算动词元胞网络模式的分类和统计信息和右及自身影响。在论文中研究了二维计算动词元胞网络，在本文中，我们将研究一种新型的二维计算动词元胞网络模式——菱形对称波模式。

本文提出新型的计算动词元胞网络模式——菱形对称波模式，又分为典型性和非典型性两类，在除图像处理上有应用，也在农业，电子等领域有着重要的研究价值。刘文华等人发现菱形冲击波在水利研究中有着重要的科研价值，蔡秀梅等人利用菱形结构设计新型滤波模板，在指纹识别上有良好的应用价值，沈飞等人提出利用菱形的新型曲折线慢波结构来处理电子束，刘光鑫通过对球面菱形网格系统实现在球面菱形网格网上集成和管理中国海潮系统模型相关数据，所以菱形对称波模式的发现对研究二维计算动词元胞网络有推进式的发展。

本文的安排如下：在第一部分，为本文的研究背景及简介；在第二部分，解释二维计算动词元胞网络的原理等；在第三部分，研究典型性和非典型性菱形对称波模式计算动词元胞网络；在第四部分，得出本文的结论及展望。

1 二维计算动词元胞网络

就算动词元胞网络是局域规则是计算动词规则的细胞网络，每一个细胞只和它的邻域细胞相互直接影响。

广义的计算动词元胞网络由于存在空间变化而有很强的非线性和结构上的复杂性所以难以对其进行。我们只着力于计算动词元胞网络及它在整个网络中的邻域的空间变化，

我们用一个m*n的网格来表示二维计算动词元胞网络，表示第i行第j列的细胞的二维计算动词元胞网络为Cij。假设细胞Cij的状态是Xij。细胞Cij的邻域是Nr（i，j）。对于摩尔邻域，我们设定细胞中心距离r=1，Xij的进化过程基于计算动词规则如下：

2 二维计算动词元宝网络菱形对称波

在之前的计算动词元胞网络研究中，都是针对随机初始来获得模式图案，本文研究创新点是在特定初始值情况下由混沌状态演化为稳态模式的情况。采取6.24是因为在1与10之间的一个随机的中心元胞状态值，更能有效地模拟出菱形对称波的CVCN模式。

试验环境：网络大小是64×64，初始条件：整个网络除中心元胞状态值为6.24外，其他元胞状态值都为0。

2.1典型性二维计算动词元宝网络菱形对称波

典型性二维计算动词元胞网络菱形对称波是严格按照菱形对称模式存在的波形，通过菱形波来和邻域细胞产生相互影，形成稳定的菱形对称波。

设置动词矩阵V后，利用特殊值Pi，Ps，和Pd得到二维计算动词元胞网络菱形对称波。维度为15*10。

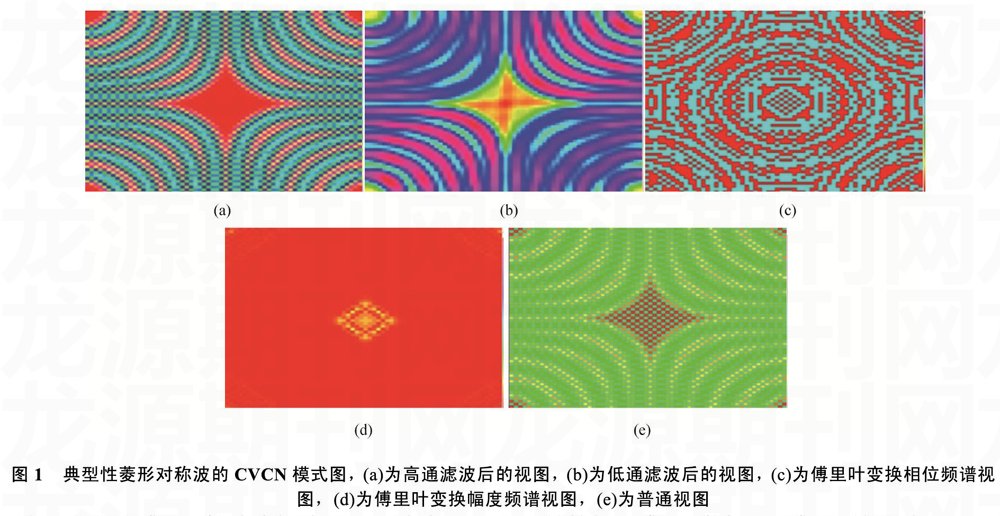
设置参数为Pi=2.79696，Ps=-9.92491，Pd=-3.85904，图（1）如下所示：

产生的各项参数如表1和图2所示。在迭代次数达2042次时达到典型性二维计算动词元胞网络菱形对称波的图案。

2.2非典型性二维计算动词元胞网络菱形对称波

非典型性二维计算动词元胞网络菱形对称波是相似性的按照菱形对称模式存在的波形，通过菱形波来和邻域细胞产生相互影响。

设置动词矩阵V后，利用特殊值Pi，Ps，和Pd得到二维计算动词元胞网络菱形对称波。维度为15×10。

设置参数为Pi=2.79696，ps=-9.92491，Pd=-3.85904，图（2）如下所示。

产生的各项参数如表2所示。在迭代次数达2042次时达到典型性二维计算动词元胞网络菱形对称波的图案。

非典型性二维计算动词元胞网络菱形对称波又包括扩散式和融合式，图4和图5分别体现出来两种类型的低通滤波图和高通滤波图。

3 结论

在本文中，我们利用计算动词元胞网络模型对菱形对称波进行建模，有典型性和非典型性两种模式，通过简单的设置便能利用计算动词理论来计算复杂模型或图案。将非线性系统与计算动词系统联系起来对科学系统中的各种应用模型进行建模，并且今后菱形波将越来越多地应用到科学研究中。然而，利用计算动词元胞网络来建模的主要困难是模型多变，并且在相同的计算动词规则下，我们可以改变动词的权重来得到不同的菱形波或其他的可模拟的波形。

目前，二维计算动词元胞网络的研究只是在表面较浅的程度，今后的研究工作是如何通过可视化来探索形成动词元胞网络模式的特性规律。我们希望本文可以为今后的元胞网络研究提供一个方向。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。