《基于改进粒子群算法的机位分配问题研究》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于改进粒子群算法的机位分配问题研究

范文

陈骁睿

摘要：为提高机场的运营效率和保证客户的满意度需要合理进行停机位分配工作。经详细分析机位分配问题的要素和约束条件，以停机位使用最均衡以及旅客的行走距离最短为目标建立分配模型，选定粒子群算法对其初始化及迭代步骤进行改进，对模型进行求解，编码设计出可拖拽的机位分配系统，采用模拟数据方式证明本改进算法提高了分配效率。

关键词：计算机应用技术；粒子群算法；机位分配模型；图形化系统

中图分类号：V351.11

文献标识码：A

0 引言

随着经济发展对航空业业务量和服务质量要求越来越高，机场的基础设施容量不足逐渐成为发展的掣肘，而对核心资源停机位的最大化利用的研究也就刻不容缓。从长远发展的角度，解决停机位资源紧缺最简单的办法是增加硬件设施投入，但考虑到开销较大，周期较长，影响因素较多，需要充分调研，不能解决于一朝一夕。而结合现有停机位并未充分利用的现象，当前的最实用策略，就是最大化挖掘潜力，通过智能化信息化方法合理分配停机位使用，确保机场的高效运转，提高旅客的满意度，此研究具有重要的现实意义。

机位分配问题是一个NP问题，同时具有复杂的约束条件，问题规模较为庞大，很难找到精确的最优解。对于此问题，国外目前的研究主要分为数学规划，计算机仿真和专家系统三个方向。Bailey提出了一个最小化旅客到达相关航班的时间的方案，采用启发式禁忌搜索办法，模拟成混合0-1规划问题，取得较好序列。而S.GHamzwawi采用计算机仿真的方法，模拟机场环境，得到机位预分配方案。此外，G.D Gosling等学者进一步考虑各种约束条件，各自建立了改进效率的专家系统。国内学者张晨等也从航班延迟，容量计算等不同角度扩展了问题研究思路。本文在其基础上，探讨了改进算法的运行效率，以及现实使用性等，分析机位分配问题因素，结合改进粒子群算法建立分配模型，最终设计出机位分配系统，并进行数据模拟验证。

1 问题分析及模型构建

1.1问题分析

停机位分配问题是将航班时刻表，停机位资源情况，航班情况等综合考虑，为未来一段时间内到达的航班预分配好适当的停机位，保证机场的稳定高效运转以及旅客的安全平稳进出。本文选取旅客行走时间最短与机位均衡使用为优先目标，设计出高效的分配算法，实现可实时自动分配机位的系统，确保机场运营效率和旅客体验双标准。

机位分配问题中的约束是由航班和停机位两者相互影响产生的。航班影响分配结果的属性主要有，一是航班号，确定航班唯一ID。二是航班的路线，可分为国内，国际，地区航线等。三是航班的机型，目前按大小主要分为A-F六类飞机，本文简化为大，中，小三种机型。四是航班的到港和离港时间，考虑旅客上下机，加油，进出机位多种时间因素，一般大机型停留时间较长，小机型比较快捷。而停机位的主要属性包括，一是停机位唯一标识。二是根据距离航站楼远近分为近机位和远机位，近机位服务质量高，由廊桥即可进入，远机位需摆渡车接送乘客，体验较差。三是停机位的大小，依据航班的标准，也分为大中小三种。四是机位的启用情况，只有已启用机位方可使用。

本文模型在以下假设前提下进行了抽象，选取最主要问题进行剖析。一是选取有限时间范围，因停机位分配是个连续的过程，本文只考察某段时间内分配情况，对问题并无影响。二是假设机场容量充分，假设停机位及其配套设施足以满足航班进离港的需求。三是航班配对假设，即一个到港航班必对应一个离港航班，使用配对的航班号。

可以分析出这是一个多目标多约束的模型，具有复杂的求解特性，有解时具有巨大的解空间，随着停机位及航班序列的增长，问题难度会成阶乘级增长。传统的数学规划等方法很难高效的求解问题，而本文设计的改进粒子群算法收敛快，遍历范围广，很适合求解机位分配问题。

2.2.3更新策略

用以上适应度函数即可求得每个粒子的适应度值，进而比较出个体极值pbest和全局极值gbest。因机位分配问题设计中采用离散编码，对于连续性的速度位置更新策略很难表示。本文引入遗传算法的交叉，变异策略，将变异看成对保持本身速度惯性的改变，将交叉看成粒子对个体极值与全局极值的靠拢程度。

在变异操作中，从粒子的分配序列中，随机选择一个变异点h1，从它的可分配机位集合Availablei中随机选择一个可用机位。如果没有可用机位的话，选择不变异，保证该粒子依旧满足约束。

在交叉操作中，需要将每个粒子分别于其个体极值和总的全局极值进行交互，符合粒子群算法追踪最靠近最优解的粒子来寻找最优解的特性。从粒子中随机选择两个变异位置c1和c2，将其间的序列片段与个体极值和全局极值分别进行交互。

在交叉操作后，改进算法设计一种调整策略，对交叉产生的不可行解调整成可行解，同时也扩大了搜索范围，避免算法过早陷入局部最优解。从交叉操作的起始位置c1开始，一直纵深向下搜索，采用初始化中的回溯法结合随机法，直到找到可行解为止。

为提高效率，使得向最优解收敛加快，本算法设计在每个粒子发生交叉变异操作后，即刻对操作后的粒子适应度值fitness1与pbest和gbest进行比较，采用实时更新策略改变两个极值，使得本算法更新速度更快。

2.2.4算法终止

当达到迭代次数iteration后，即退出算法，当超过一定迭代次数后，算法的gbest值会趋于稳定，此时也代表找到了最优解。此时种群中的所有粒子应都趋于一个位置，而此时的全局极值gbest的粒子，即为最终所求的最优航班分配序列。

3 展示及模拟数据分析

3.1结果展示

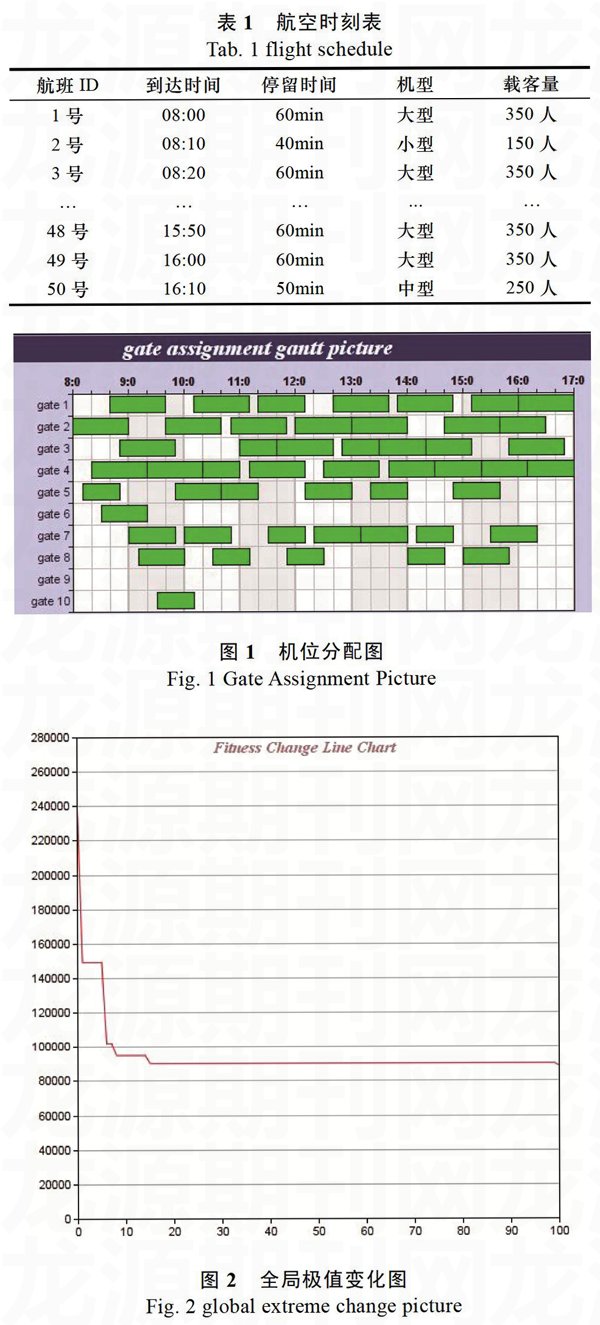
以某机场运行现状进行同比缩小后，对机位分配问题中各项数据做出如下设定。设定一共有10个可用停机位，其中4个为大型机位，4个为中型机位，2个为小型机位。而前5个设定为近机位，后5个为远机位。假设问题时间段为从早8：00至下午5：00，共9个小时，航班到达时间皆在此时间段内，停留时间超出部门截取掉不计。9个小时内，配对航班总共为50架次，以每10分钟一架次的频率到达，机型数据按规律模拟随机产生。

可见航班时刻表如表1。

程序中，种群大小设定为10，而迭代次数取值100次，多次试验证明此时结果基本趋于稳定。算法中两个目标，旅客行走距离最短必然使得靠近航站楼的机位会使用更加频繁，而均衡使用的目标使得远侧机位也能得到充分利用，这两个目标本身具有一定矛盾性，所以权重系数α有侧重选取，本文使行走距离最短目标占0.8，均衡使用目标占0.2。

3.2结果分析

可见，在机位分配结果中，由于选定行走距离最短为主要目标，靠近航站楼的停机位都得到了充分利用，有效缩减了旅客的行走时间。而对于均衡使用目标，可见大部分停机位都得到了充分利用，由于小型机较少，而且利用前面机位能得到更优质的服务，使得空间时间方差和得到有效降低。

改进算法中，通过观察gbest的变化，可以分析出算法的性能。本改进粒子群算法的全局极值变化如图2。

可见改进算法可以取得快速的收敛，在20轮迭代左右即趋于稳定，而改进算法的适应度值也得到了大幅度的降低，找出了最优解。说明本算法从效率和可行性上都取得了不错的成效。

4 结束语

本文从提高机场运营效率和增加旅客满意度两个角度出发，分析了机位分配问题中航班和停机位的影响因素，抽象出约束条件和目标函数建立了机位分配问题的数学模型。因为粒子群算法在解决此类问题上快捷，有效的特点，结合机位分配问题独有特性，对算法中各个步骤进行改进，提高了分配效率。设计出图形化的机位分配系统，采用可拖拽的方式简化操作人员的难度。最后模拟数据对算法的可行性进行验证，表明改进的粒子群算法可以快速，有效地完成机位分配工作。因研究时间尚短，还有很多改进工作和方向可以在今后深入研究与探索。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。