《小波分析和支持向量机在供水短期负荷预测中的应用》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

小波分析和支持向量机在供水短期负荷预测中的应用

范文

闫江宝+谭向宇+张长胜+赵振刚+李川

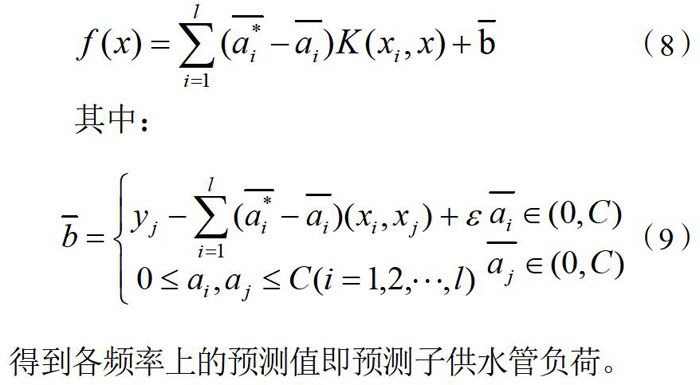
摘要：本文运用支持向量机具有训练时间短、结构风险最小化、全局最优、泛化能力强等优势，将其应用于供水管网短期负荷预测；利用小波分析在时频分析具有跟踪时间和频域信息的优势，同时联合支持向量机的优势，将此预测算法运用到供水短期负荷预测系统中，实现了算法的实际应用。

关键词：供水管网；短期负荷预测；小波分析；支持向量机

0 引言

城市用水量预测是供水网络分析管理的重要组成部分。供水系统负荷预测的准确性直接影响供水优化调度的可靠性和可用性。供水管网系统中供水负荷的变化无论从微观上还是从宏观上分析都受到很多因素的影响，如何既能够预测突发负荷变化又能够预测负荷变化的主要趋势成为一直以来的难题，恰好小波分析刚好能够承担起这方面问题的处理者。

供水管网水量具有特殊的周期性和随机性，利用小波变换将符合序列分解到不同的频率段上，分为低频分量和高频分量两个部分。可以根据实际需要选择分解尺度，得到各个尺度上的负荷子序列，再根据不同负荷子序列的周期性和特点，有针对性的建立负荷预测模型，最后通过重构，得到完整的负荷预测结果。

1 小波变换

小波变换是在二十世纪七十年代首先提出来的，是继传统傅里叶变换之后提出的一种新型算法小波变换改进了傅里叶的缺陷，提供了一个可以变化的时间一频率窗，能获得时间空间频域的局部化信息，达到高频位置时间细分，低频位置频率细分，在科学领域具有重大突破。

小波是指在-∞，+∞上振荡，振幅很快衰减的一类函数，设Φ t∈LR，且满足允许条件：则Φt 成为一个基小波，对于一个给定的基小波Φ （t），令：

其中a∈R-{0}，br，a称为尺度函数，1/a相当于频率，b称为定位参数。

设ft∈LR是有限能量函数，积分核表示为函数族Φab（t），那么f'（t）的连续小波变换如下式3所示：

Φab（t），称为小波变换的原子，其具有白适应性，能提取局部信息，同理，小波变换具有逆变换：由Parseval定理，得到：

假设Φ（t）的时域重心和半径为t*和VΦ（t），（t），，频域重心和半径为w*和VΦ，则Φab（t）的时域重心和半径为a（t*+b/a）=at*+b和a△ψ，频域重心和半径为ω*/a和△∧/a，则时域和频域窗口分别为：显然视频窗口的面积是常数4△Φ△因而能够生成自适应窗口，小波变换通常被称为数学显微镜。

2 支持向量机

支持向量机（Support Vector Machine，SVM）[9，10]是二十世纪中期提出的一种新的机器学习技术，此技术建立在统计学的VC维理论与结构风险最小化原则的基础上，按照Mercer核定理，采用了非线性映射方法用于处理样本空间并将其映射到高维特征空间。在高维特征空间中，线性学习机用于解决样本空间的非线性分类问题。此思想方法与传统的线性模型比较，不会让计算很复杂。子空间包涵了不同的模式样本，满足了最优超平面离其最近的样本到其距离最大。支持向量通常被指定为与超平面最近的样本，并且该对应模型被称为支持向量机模型。支持向量机模型可以得到全局的最优寻求过程，并且适用于小样本问题，解决非线性、高维数带来的干扰。

支持向量机（ SVM）方法可用于建立一个令人满意的短期负荷预测模型，可用于预测短期负荷，具有良好的适用性和较高的预测精度。

3 基于小波分析和支持向量机供水短期负荷预测

3.1 建立供水负荷预测模型

将基于小波和支持向量机的供水负荷预测步骤分为五部分：

（1）首先，获取历史供水负荷数据，进行预处理。供水管网短期负荷预测需要大量的历史数据作为计算的基础，历史负荷序列可以选择每隔半小时或者一小时为间隔单位的离散负荷序列，同时还要求具有日周期性、周周期性、月周期性、季度周期性及年周期性。对数据中的供水管负荷分量进行小波频域分析：将各种供水管的负荷影响因素作为输入量，将待求的供水管负荷作为输出量，建立预测样本集。

（2）选择haar小波基函数利用训练样本中的负荷数据组成时间序列，并对时间序列进行小波频域分析。对小波分解以得到负荷子序列l和负荷子序列2。

（3）对每个负荷子序列执行SVM训练，建立SVM的目标函数，为每个频域中目标最小化的目标函数建立最优解，并将最优解代人回归函数中确定回归决策函数。

（4）求得最优解a=（a1，a1，al，...，al），代入下式，得到决策回归方程。

其中：

得到各频率上的预测值即预测子供水管负荷。

（5）通过预测子供水管各频段负荷的预测结果进行小波重构，预测供水管负荷。流程图如图1所示：

小波变换应用于供水管网负荷预测的优点表现出来得比较的明显，经过小波变换得到不同的负荷子序列，然后根据每个负荷子序列的不同周期特性分别建模预测，这样预测精度能够得到很大程度的提高。

将小波分析應用于供水管网短期负荷预测时，选取一个合适的小波函数是非常重要的。由于小波函数的多样性，当选择不同的小波函数时，相同的工程问题将有不同的解决方案。由于双正交小波具有良好的对称性和线性相位，在对负荷序列进行分解和重构时不易失真，而且双正交小波能够同时满足线性相位和正交性的要求。如图1所示，选择morl、bior、mexh、haar四种小波基函数并结合支持向量机作为供水管负荷预测算法，预测准确性最好的是选择haar小波基函数准确率达到0.98%以上；如图2所示，用SVM和神经网络算法对预测准确率作比较，在样本数一样的情况下，支持向量机的预测准确性要优于神经网络算法。

3.2 对城市供水负荷预测

为了验证本文提出的基于小波和支持向量机的供水负荷预测的有效性，本文以云南某地区的供水负荷为例，采用2011年10月至11月的数据建立采样，并以2011年10月30日进行10次负荷测试，验证预测精度。获得以下历史负荷数据用于预处理。

为了比较，采用小波和SVM负荷方法，BP神经网络方法和一般SVM负荷预测方法预测2012年3月19日，全天24小时的负荷。预测结果和各种预测的预测误差方法分别如图4和图5所示。比较各种预测方法和实际负载曲线的结果曲线，如图4所示（其中x轴显示连续24个负荷，v轴负荷）。

上面结果显示：图4中小波支持向量机的预测结果更接近实际负荷。图5中从预测均误差和最大预测误差来看：支持向量机均误差是2.59小于BP预测算法的3.38，支持向量机的最大误差6.46小于BP预测算法的10.31；从预测时间来看，SVM的预测时间6.25s小于BP预测算法的l6.56S。证明SVM预测算法优于神经网络预测算法。

由以上的数据曲线可以看出小波支持向量机负荷预测模型的优越性，仿真结果表明了联合小波和SVM负荷预测的算法，显著提高了供水短期负荷预测的精度，说明本文所提出的基于小波和支持向量机的供水负荷预测模型是有效的。

4 结束语

供水管负荷预测是管网系统安全运行的重要环节，因为供水负荷预测的相关因素复杂，具有非线性，所以只用一种负荷预测很难实现对预测精度的挺高。对数据进行相应的处理，加强其可预测性，同时是降低预测时间的一种好方法。本文采用小波频域分解对历史供水管网负荷序列进行分解，小波频域分解后的负荷序列的可预测性显著提高。由上述仿真结果证明本文利用小波分析与支持向量机回归相结合的方法有效性，可以实际运用于供水管网的负荷预测。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。