网站首页  词典首页

请输入您要查询的论文：

　

标题 基于神经网络的建筑物稳定性时间预报分析
范文 何群
摘要：利用神经网络对GNSS数据进行高程异常拟合处理，以地铁地表沉降二等水准数据为检测数据，对拟合后的精度进行评定。在神经网络预测中，神经元的选择以及训练函数的确定，对建筑物稳定性评价起到关键作用。
Abstract： The neural network is used to fit the elevation anomaly of GNSS data， and the second-level data of subsidence of metro surface is taken as the test data to evaluate the accuracy of fitting. In neural network prediction， the selection of neurons and the determination of training function play a key role in the stability evaluation of buildings.
关键词：神经网络；建筑物稳定性评价；高程异常拟合
Key words： neural network；evaluation of building stability；abnormal elevation fitting
中图分类号：TU196+.1 文献标识码：A 文章编号：1006-4311（2018）12-0171-02
GNSS定位系统是大数据信息化的一个获取地球表面信息的重要手段，由于其具备便捷的的操作方式、高等级的测量水准，在大数据时代的生产领域得到充分利用。将GNSS定位技术与局部范围内地球重力资源、精密水准资源和高分辨率的地形数据资源加以整合，可以解决GNSS定位技术自身无法直接提供准确正常高的弊端，从而精确地获得局部范围内高程异常可靠值。
水准正常高主要应用于建筑物施工过程，建筑施工测量中正常高的获取方法通常是利用水准测量来满足生产的需要，但由于需要在外业进行长时间的观测，受外界自然条件影响的因素较多。而GNSS观测技术已经攻克观测时受外界条件影响的各项弊端，精确测定正常高成为GNSS定位系统的一项技术难点。
GNSS定位系统的静态精度已经可以达到0.5毫米以下，相对而言，高程定位精度较低。由于GNSS高程测量系统中的大地高是基于一个相对特定参考椭球，和建筑工程测量中广泛应用的正常高具有不同的参考基准。如果获得两者之间的转换参数（水准面差距或高程异常），并构建相应的高程系统转换模型，从而将GNSS定位系统的大地高转换为水准正常高。
对于建筑物稳定性时间预报系统的构建，需要根据具体的监测项目数据利用神经网络模型构建适合高程异常转换的神经网络BP预测模型。
神经网络BP预测模型是具有多层神经元的传统经典神经网络，正常情况下预测模型可以由输入层、中间层和输出层组成。第一阶段信号传播过程如下：前后层间可以实现网络神经自由连接，而自身层各神经元间是没有信息沟通的。当学习样本赋予给神经网络后，神经元的激活值从前一层经中间层向后一层正向传播，输入响应在输出层各神经元间产生，并完成第一阶段信号正向传播。第二阶段信号传播过程如下：依据产生最小输出误差的原则，从最后层经过若干中间层反向传输至第一层，并逐层修改各连接权值，即“误差反向传播算法”，完成第二阶段的信号反向传播。
从理论上分析建筑物沉降变形监测是GNSS平面坐标（或大地坐标）到高程异常（或正常高）的转换，利用神经网络BP模型进行完成GNSS高到水准高的预测，需要构建的BP神经网络结构应该是A×M×B的结构。
以某地铁地表监测资料为样本来源，进行高程异常拟合。根据区间自身风险及环境风险，监测等级采取“就高不就低”的定级原则，综合判断，本区间联络通道及左右线下穿浑河段监测等级为一级；其它区间段监测等级为二级。为验证神经网络BP模型预测的精度满足地铁地表沉降观测的需要，进行如下实验：
实验一：
将外业观测数据选择6个点作为学习样本，9个点作为测试数据，BP神经网络中间层设定12层，网络目标中误差0.0001m。分别采用梯度下降法（traingd）、拟牛顿算法（trainbfg）、动量及自适应lr的梯度下降训练法（traingdx）、Levenberg-Marquardt训练法（trainlm）进行BP神经网络拟合模型训练，实验结果如表1。通过实验一可以得出GNSS高程异常神经网络BP拟合模型的训练函数最优选择是traingdx函数。
实验二：
将外业观测数据选择8个点作为学习样本，7个点作为测试数据，BP神经网络中间层分别设定为6、8、12、15、18、20层，输出结果目标中误差0.0001米。本实验主要选用traingdx和trainlm作为网络训练函数，实验结果如表2。
结果表明针对GNSS高程异常在建筑变形监测中利用BP神经网络构建拟合模型，trainlm函数收敛速度最快，traingdx函数训练精度高。从表2中可以看出，拟合精度提高与网络神经元的数量多少有一定关系，但并非中间层神经元数量越多代表其拟合精度就越高，具体可见图1、2所示。
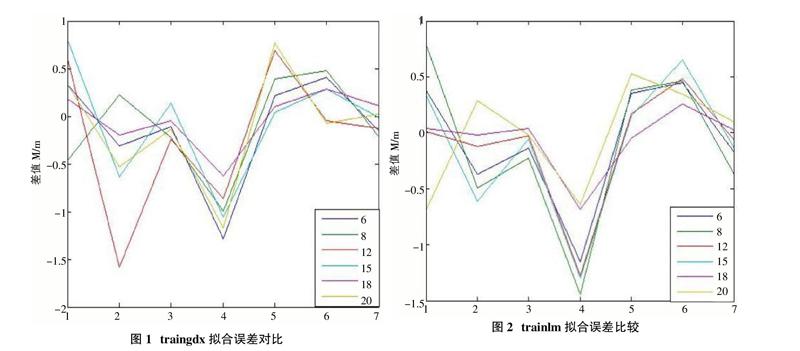
利用神经网络BP模型对GNSS高程异常进行拟合，选择什么样的训练函数对模型的收敛速率和效率都会有一定的影响。在施工场地变形监测实践中，需要根据具体的实际工程项目进行多次模拟测试，以便选择最合适的训练函数，构建最优的网络结构，以寻求经典的网络预测模型。
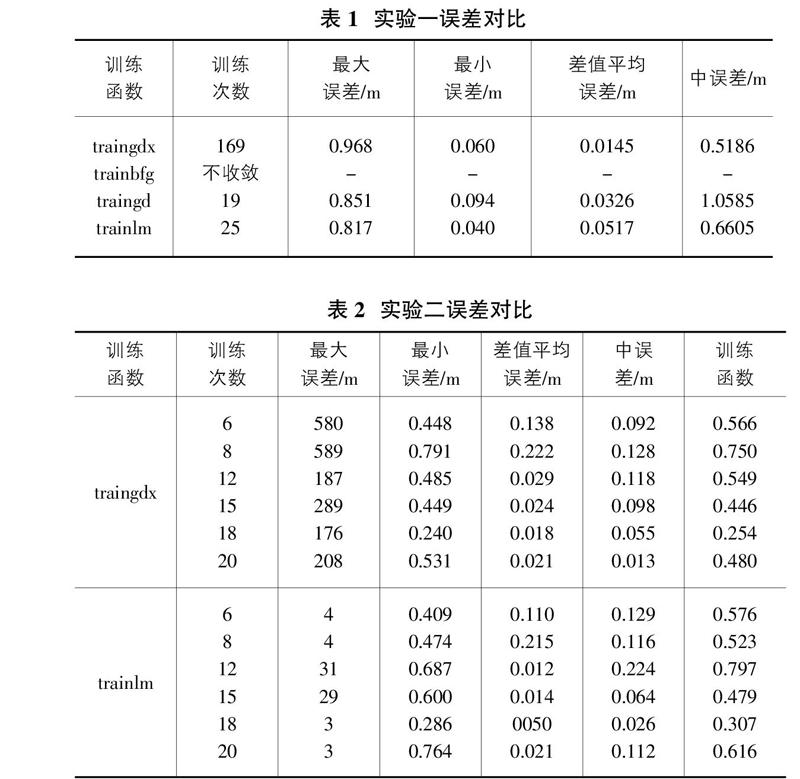
本项目结论如下：
①通过对GNSS大地高进行变形监测神经网络BP擬合模型转换， traingdx训练函数的 网络效率最好，trainlm 训练法收敛速率最高，建筑变形监测应结合的实际工程项目精度需要选择合理的训练函数。
②本次网络试验测试选择traingdx函数，中间层确定在16-18层之间，模型拟合精度可以满足地铁地表沉降观测的精度要求。
③实验结果表明，利用神经网络构建拟合模型完成GNSS大地高转换，在训练好网络结构模型后，可以得到比传统数学模型更高的转换精度。
④目前神经网络BP拟合模型研究在训练样本数量等方面没有明确的规定，但在本项目实验过程中发现训练样本对于提升网络的学习能力和泛化能力有很重要的影响。建筑物变形监测中当训练样本的数量和质量涵盖所要监测项目的全部特征，利用神经网络模型制定自身合理的学习方式，完成拟合模型对问题的描述。
⑤神经网络BP拟合模型的精度不仅与施工场地的似大地水准面有关，还与GNSS已知点点位和数量有关。如果已知点与似大地水准面的特征点重合度较大，则模型拟合效果就接近实际情况。如何布设GNSS已知点，是进行高程异常转换的关键问题之一。
参考文献：
[1]李建成.最新中国陆地数字高程基准模型.重力似大地水准面CNGG2011[J].测绘学报，2012（05）.
[2]谭立萍，等.三层模型的BP网络在GNSS高程拟合中的应用研究[J].测绘通报，2018（08）.
[3]朱宝训，杨波，王晓静，高宁.基于加权最小二乘的GNSS高程拟合模型分析[J].人民长江，2015（03）.
[4]占伟，黄立人，刘志广，孟宪纲.数据缺失对GNSS时间序列分析的影响[J].大地测量与地球动力学，2013（02）.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 3:43:56