网站首页  词典首页

标题	考虑结构刚度的四点接触球轴承力学建模方法与接触载荷分析
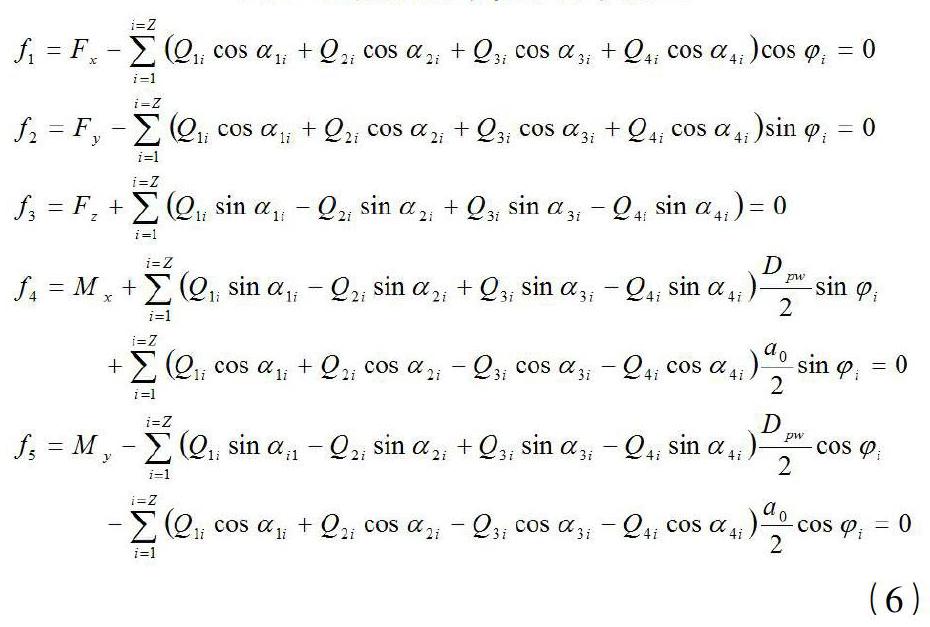
范文	李超 陈观慈 侯光辉 王存珠 温戈 摘要：本文采用数学建模的方法，引入四点接触球轴承套圈刚度矩阵，以此考虑结构刚度对四点接触球轴承内部载荷分布的影响。建立了四点接触球轴承的非线性位移和力学平衡方程，该方程可采用牛顿拉普逊方法迭代求解。以风力发电机组偏航变浆用四点接触球轴承为例进行了计算分析，验证了本文建立数学模型的计算快速性和精确性。 Abstract： In this paper， the stiffness matrix of four point contact ball bearing ring is introduced by mathematical modeling method， and the influence of structural stiffness on the load distribution of slewing bearing is considered. The nonlinear displacement and mechanical equilibrium equations of four point contact ball bearings are established， and the equations can be calculated by Newton-Raphson iteration procedure. Taking the four point contact ball bearing as an example， the calculation and analysis of the yaw and pitch bearing of the wind turbine are carried out， and the calculation speed and accuracy of the mathematical model established in this paper are verified. 關键词：四点接触球轴承；刚度矩阵；有限元；力学模型 Key words： Four point contact ball bearing；Stiffness matrix；Finite element；Mechanical model 中图分类号：TH133.3 文献标识码：A 文章编号：1006-4311（2018）19-0255-03 0 引言 四点接触球轴承套圈尺寸较大，刚性较低，轴承套圈刚性对其内部接触载荷分布影响较大，因此进行力学分析时其套圈刚性成为一个不可忽略的因素。目前国内外已经研究了关于四点接触球轴承力学建模方法和接触载荷分析的相关概念，但主要是针对不考虑结构刚度的刚性模型[1-3]或有限元模型[4-5]，而针对考虑结构刚度的四点接触球轴承力学模型研究较少。本文引入四点接触球轴承套圈刚度矩阵，以此考虑结构刚度对其内部载荷分布的影响，建立其非线性位移和力学平衡方程组，采用牛顿拉普逊方法求解此方程组。论文建立的数学模型兼顾了计算精确性和快速性，为四点接触球轴承相关参数的优化奠定了基础。 1 考虑套圈结构刚度的四点接触球轴承力学模型 1.1 四点接触球轴承力学系统 图1为风力发电机组用双列四点接触球轴承的截面图。图中：α0为轴承接触角；Dw为滚动体直径；g0为轴承游隙；Ri、Ro为内外圈滚道沟曲率半径。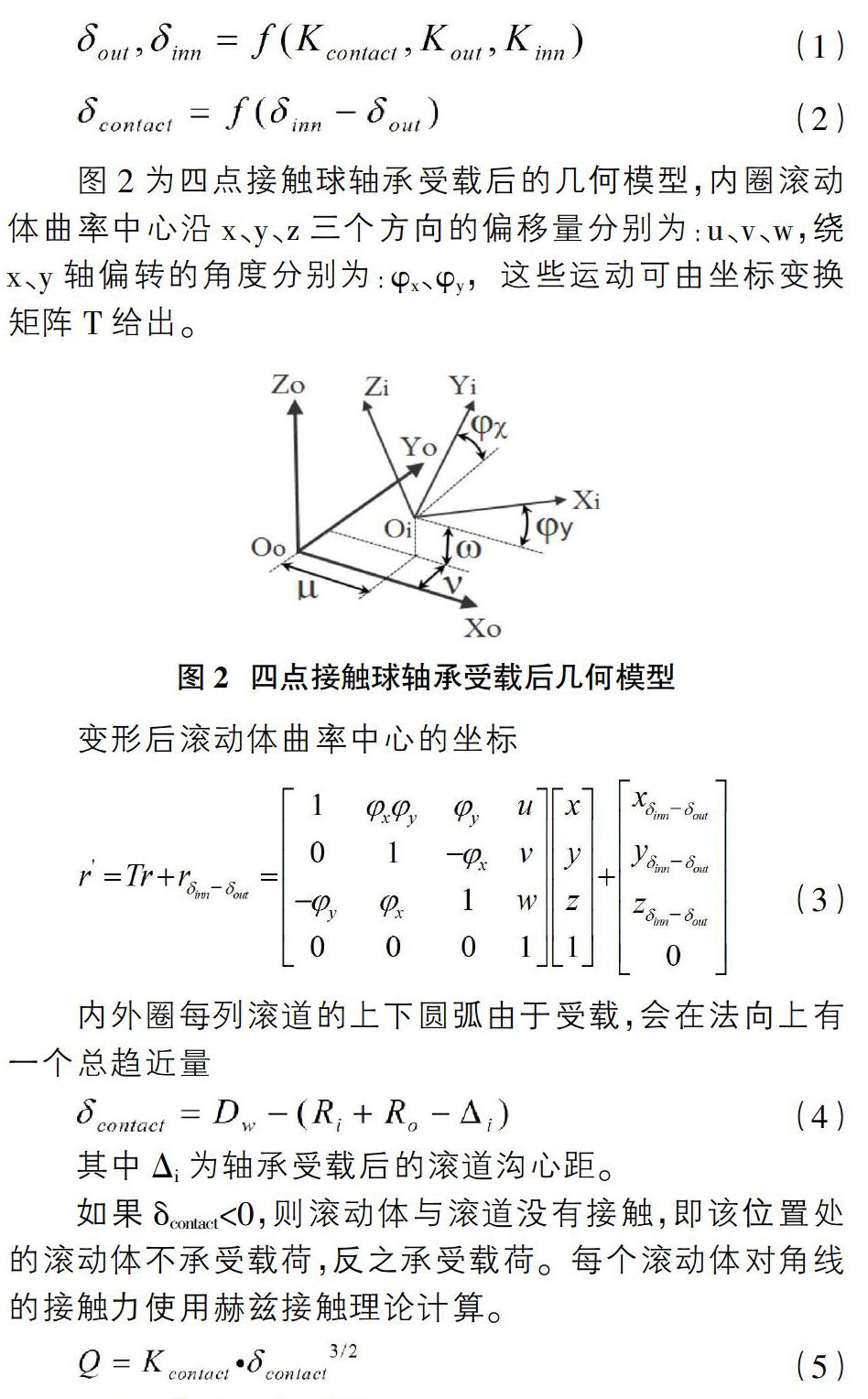 前述双列四点接触球轴承工作时的受力和变形可用三个弹簧串联表达，轴承外圈下端面固定，内圈承受外部载荷。变量Kinn、Kout代表内外圈的刚度矩阵，Kcontact是滚动体和滚道间的接触刚度，对内圈施加一个外载荷F，采用迭代程序获得平衡位置，内外圈弹性变形δinn和δout由接触刚度和套圈结构刚度共同决定。 图2为四点接触球轴承受载后的几何模型，内圈滚动体曲率中心沿x、y、z三个方向的偏移量分别为：u、v、w，绕x、y轴偏转的角度分别为：φx、φy，这些运动可由坐标变换矩阵T给出。 其中Δi为轴承受载后的滚道沟心距。 如果δcontact<0，则滚动体与滚道没有接触，即该位置处的滚动体不承受载荷，反之承受载荷。每个滚动体对角线的接触力使用赫兹接触理论计算。 1.2 平衡方程与求解 四点接触球轴承单个滚动体与内外圈滚道的接触载荷为一对平衡力，且滚动体接触载荷与套圈外载荷为平衡力，根据此原理即可建立套圈滚道接触载荷与外载荷的平衡方程，如式（6）。整个系统的力学模型可用图3表示。 其中Fx，Fy，Fz，Mx，My表示轴承承受的外载荷；φi表示第i个滚动体的位置角；αi表示轴承接触角；Q1i、Q2i表示第一排滚动体在位置角φi处两个接触面法线方向的接触载荷，Q3i、Q4i表示第二排滚动体在位置角φi处两个接触面法线方向的接触载荷。 滚动体和滚道接触载荷与轴承套圈的弹性变形相互影响，是非线性函数，因此要用图4中牛顿拉普逊迭代程序计算套圈的变形和接触载荷。 2 算例与结果分析 以某公司提供的风力发电机组偏航变浆用四点接触球轴承为例进行了计算分析，该轴承的基本结构参数和极限载荷见表2。 在相同外载荷下分别绘出四点接触球轴承在刚性模型、柔性模型、有限元模型下接触载荷和接触角分布特点，如图5和图6所示。 从图5可以看出，两沟道滚珠接触载荷分布趋势基本一致，且每列沟道滚动体所受载荷分布不均，在圆周上呈现近似正弦分布。两沟道与滚动体一半因分离而处于不受载状态，另一半因压紧而处于接触状态，大多数是两点受力，少部分是四点受力，且四点接触的滚动体承受的载荷比较小。轴承第一列滚动体对称位置承受的载荷相差较大，第二列基本一致。 从图6可以看出，两沟道滚珠接触角分布趋势基本一致，且每列沟道滚动体接触角不同，与滚动体的接触载荷分布规律一样，也成正弦分布。处于四点接触的滚动体对应的接触角相比原始接触角变小了，接触角在0°到150°承载区域内的变化幅度相对较小，在150°到360°承载区域内变化幅度相对较大。 3 结论 本文以双排四点接触球轴承为例，建立了考虑套圈结构刚度的大型转盘轴承静力学模型，建立了简化滚动体的有限元模型。且柔性模型所得结果与有限元模型结果基本吻合，其计算时间成本优于有限元模型，准确度优于刚性模型。该模型可扩展到考虑支撑结构刚度的四点接触球轴承，分析其结构刚度对其接触载荷和接触角分布的影响，并进行相关结构参数的优化设计。 参考文献： [1]高学海，黄筱调，王华，陈捷.双排四点接触球转盘轴承滚道接触压力分布[J].南京工业大学学报（自然科学版），2011（01）：80-83. [2]徐绍仁，杨友中，白宇光，王燕霜，邓四二.特大型负游隙四点接触球轴承拟静力学分析[J].轴承，2009（09）：1-3，7. [3]陈国桢，徐绍仁，杨友中，王燕霜，邓四二.特大型负游隙四点接触球轴承接触应力分析[J].机械传动，2009（05）：83-85，91，112. [4]李云峰，刘彩霞，陈红涛.双排四点接触球转盘轴承的有限元分析[J].哈尔滨轴承，2015（02）：3-6，9. [5]王存珠，陈观慈，李肖杰，温戈.螺栓及其预紧力对大型转盘轴承接触载荷分布的影响[J].轴承，2016（01）：24-27，33.
随便看	情境教学有效设问策略研究 聚焦题型减轻备考负担 优化模式提高复习效率 PISA的启示：探索从知识到素养的教学路径 关于化学课堂“有效共识”培训课程研发的思考与实践 初中生化学学习自我调节能力的调查研究 高中新课程化学实验教学现状调查报告 高一学生化学思维过程的差异及其培养策略研究 化学教学中的比较逻辑 深度学习理念下的有效教学设计 空气负离子发生器及负离子发生材料简介 解读中考化学识图题 利用“模型法”突破工艺流程图题 基于WSR系统方法论的化学实践性作业的设计 命制化学实验探究原创试题的实践与思考 增进中学化学作业交流功能的实践与思考 例谈重视化学实验的细节问题 例谈初中化学实验教学中培养学生控制变量思想的方法 发展学生思维品质的初中化学实验教学策略 二氧化锰的用量对双氧水分解反应的影响初探 补注区别浓硫酸和稀硫酸的方法 钠与硫爆炸反应实验的设计 几个初中化学趣味实验及相关探究课题 二氧化硫溶液与氯化钡溶液反应实验的改进 一种新的海带提取碘的实验方法探析 突破衍射极限——探索纳米世界的超分辨显微技术 rebaiting rebaits rebake rebaked rebakes rebaking rebalanced rebalances rebalancing reballot reballoted reballoting reballots reban rebandage rebandaged rebandages rebandaging rebaptisms rebaptized rebaptizes rebaptizing rebarbarization rebarbarize rebatable, rebateable 云梁 云梢 云梦 云梦之台 云梦伪游 云梦闲情 云梯 云楣 云楶 云楼 云概念 云榭 云榻 云横秦岭 云樽 云次鳞集 云欲断 云歌 云步 云步石梯 云殿 云母 云母冠 云母帐 云母的一种

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。