网站首页  词典首页

请输入您要查询的论文：

　

标题 基于CCGA—BP的凌情预报模型研究
范文 李福川+王富强+裴颖新+李宗霖

摘要：凌汛是河道里的冰凌对水流的阻力作用而引起的一种涨水现象，它直接影响到水利工程的运行和维护、水利发电、冬季输水等问题，较高精度的凌情预报成果可为防凌减灾提供重要决策信息。针对遗传算法优化神经网络时不能同步优化网络结构和连接权值且计算量大的问题，采取分而治之的思路构建了基于合作型协同进化遗传算法的BP神经网络（CCGA-BP）凌情预报模型。运用MATLAB2009b进行建模，并将其应用于宁蒙段巴彦高勒封河日期的预报，结果表明，CCGA-BP模型历史样本拟合合格率达到89.3%（25/28），预报检验合格率为100%（5/5）。预报模型可以用于黄河宁蒙段冰凌预报实践。
关键词：凌汛；凌情预报；封开河日期；CCGA-BP；宁蒙河段
中图分类号：P338文献标志码：A文章编号：
1672-1683（2015）001-0207-04
Study on the ice condition forecasting model based on CCGA-BP
LI Fu-chuan1 ，WANG Fu-qiang2，PEI Ying-xin3，LI Zong-lin1
（1.South-to-North Water Diversion Project eastern shandong co.，LTD ，JiNan 250013 China；
2.North China University of Water Conservancy and Hydroelectric Power，Zhengzhou 450045 China；
3.Material company？of Liaohe Petroleum Exploration Bureau，Panjin 124000 China）
Abstract：Ice flood is a freshet phenomenon caused by the blocking effect of ice in the river channel，it will directly influence the operation and maintenance of water conservancy project，hydroelectric generation and water delivery in winter，etc.High-accuracy ice forecasting achievement can provide important decision information to ice flood control and disaster mitigation.To counter the problem that genetic algorithm cannot optimize network topology as well as connection weights and has a large amount of calculation when optimizing neural network，this paper，based on the co-evolutionary genetic algorithm，first take the policy of divide and rule and set up the BP neural network（CCGA-BP） ice forecasting model.Then use MATLAB 2009 b and applied the model to the forecasting of ice-locked date in Bayangol，Ningxia-Inner Mongolia reach.The results show that the historical sample fitting rates reach 893%（25/28），and the prediction test passing rate is 100%（5/5）.Thus the forecasting model can be put into practice in Ningxia-Inner Mongolia reach of Yellow River.
Key words：ice run；ice condition forecasting；ice-locked and break up date；CCGA-BP；Ningxia-Inner Mongolia reach
黄河以冰凌灾害频繁而著名，每年封开河都要发生不同程度的卡冰结坝现象，由此造成冰凌灾害频发[1]。冰凌的出现往往危及桥梁、河道工程和其他水工建筑物的安全。因此黄河宁蒙河段的冰凌研究对于冰凌灾害防治具有重要的实践意义[2-3]。长期以来各有关部门的科研人员对冰凌现象进行了大量的预报研究。国外对封河、开河日期预报研究较多的是美国Clarkson大学的沈洪道教授[4]，主要依据热交换原理和冰水力学理论建立了数学模型。国内不少学者依据黄河的原型观测资料建立了一系列的冰凌预报模型。可素娟等于1998年建立了黄河上游实用冰情数学模型[2-5]；2004年陈守煜教授提出的模糊优选神经网络BP模型对黄河内蒙段封河、开河日期进行了预报[6]；2007年姚惠明对黄河宁蒙河段凌情特性进行了研究，并分析了宁蒙河段1950年—2004年流凌、封河、开河日期特征值[7]；2012年韩宇平、周翔南等提出了基于粒子群算法的神经网络在冰凌预报中的应用 [8-9]，提出了一种基于遗传算法优化支持向量回归参数的冰凌预报模型，建立了PSO-BP预报模型。
遗传算法是近年迅速发展的一种优化算法，它具有并行搜索和全局寻优的特点，广泛应用于神经网络的优化问题中。但是却只能完成神经网络权值的优化，不能进行网络结构和连接权值的同步优化，并且计算量大。人工神经网络的结构设计没有系统的规律可循，而且神经网络参数优化又易于陷入局部最优解。为了解决传统遗传算法优化神经网络时所存在的问题，本文将合作型协同进化遗传算法（Cooperative Co-Evolutionary Genetic Algorithms，CCGA）引入网络优化中。采用分而治之思想把复杂的问题分解成若干较简单的子问题，对每个子问题进行优化，最后把子问题合并形成完整的解。根据Kosmogorov定理，合适的网络结构和连接权值可以使三层前馈神经网络以任意精度逼近任意的连续函数，因此本文以三层BP神经网络为基础，建立基于合作型协同进化遗传算法的BP神经网络（CCGA-BP）的冰凌预报模型。
1基于协同进化遗传算法神经网络设计
1.1合作型协同进化遗传算法
合作型协同进化遗传算法是基于共生机制的解决复杂多变量问题的优化方法。其与传统遗传算法最大的不同是可以同时优化隐含层数已知的神经网络的连接权值和隐含层节点数，大大减少计算量。作为一种新的全局优化搜索算法，搜索过程作用于编码了的个体。所以它没有求导和函数连续性的限制，具有鲁棒性、随机性、全局性以及适于并行处理的优点，在分类、约束满足、优化调度、聚类等领域的应用上展现了它特有的优势。
该法进而将优化问题分割为多个子种群，通过各子种群间相互合作协同进化，由进化子种群构成一个完整的优化过的神经网络。相比粒子群优化算法（Particle Swarm Optimization，PSO）模型，CCGA-BP模型在优化连接权值的同时也优化了网络结构，减少了神经网络冗余的隐含层节点，其优化性能更高。
1.2基于CCGA的BP神经网络设计
利用协同进化遗传算法对神经网络进行优化，首先要进行种群分割，把目标问题分割为若干个子种群。本文对神经网络进行纵向分割，如图1所示，在一个已知为N+1层的BP神经网络中，将输入层至第一个隐含层之间的部分当做第一模块，第一层隐含层至第二层隐含层之间的部分当做第二模块，以此类推。对于每一个模块，分别用一个进化子种群优化其连接权值和网络结构（节点个数），将这些进化子种群记为P1，P2，…，PNp。
图1进化种群分割
其次要进行变量编码。以神经网络的第p个模块为例。由于神经网络的层数N+1以及输入和输出的向量个数已知，所以对网络结构进行优化就是隐含层节点的数目和节点之间的连接关系。本文对该模块的网络结构使用二进制编码，对连接权值使用实数编码，下面将分别进行分析。
（1）结构编码。
将第p层包含的节点数记为Np，用矩阵SpNp+1×Np表示第p个模块的连接关系。如果元素Sp（i，j）=1则第p层的第i个节点与第p+1层的第j个节点之间存在连接关系；如果Sp（i，j）=0，则第p层的第i个节点与第p+1层的第j个节点之间不存在连接关系。SpNp+1×Np表示第p个进化子种群个体的结构编码，把此矩阵展开即为该进化子种群网络结构的二进制编码。
图2所示的三层BP神经网络，各个层的节点数分别是2，3，1。将这个BP网络分割为两个部分，分别采用两个进化子种群优化这两个部分。
图2BP神经网络的编码
第一个进化子种群个体的结构编码是S1=111011，等价于二进制串11 10 11；第二个进化子种群的个体结构编码是S2=[111]，等价于二进制串111。
（2） 连接权值编码。
连接权值的编码要受到结构编码的控制，只有当结构编码为1时，两个节点之间才存在连接关系。如果两个节点之间不存在连接关系，就没有必要对该连接权值进行编码。因此，连接权值编码的长度应与结构编码中1的个数相同。随着进化的不断进行，结构编码中的1的个数是不断改变的，连接权值编码的长度也是随着进化的不断进行而不断变化。这种动态编码方法可以极大地降低算法计算的复杂性，从而使网络训练变得比较简便，提高了算法的性能。
仍以图2为例，不难得到，第一个进化子种群个体的连接权值编码是（02，04，-02，01，03）；第二个进化子种群的个体的连接权值编码是（01，-01，02）。
最后是交叉操作。由于结构部分的编码采用二进制编码方式，因此可利用标准遗传算法中的交叉操作来进行单点交叉或者多点交叉等；连接权值的部分采用实数编码，并且其实数编码的长度与结构编码中1的个数相同，所以，连接权值部分的交叉点依赖于结构部分交叉点位置，即实数编码交叉点前的编码串长等于其对应的二进制编码串交叉点前1的个数，这种交叉操作称为对等交叉。
假设某个进化子种群的两个父代个体，它们的基因型如表1中a列所示。对于其网络结构部分，选择第4位为交叉点，即001 1|01 100；101 1|00 111。经过交叉操作，其子代个体结构编码变为001 100 111；101 101 100。连接权值编码串交叉点的选择如表1中b列所示，经过交叉操作，其子代个体的连接权值编码变为（-03 03 -01 03 02）；（-02 01 04 -01 04）。交叉操作之后的子代个体基因型如表1中c列所示。
在神经网络的优化过程中，进化子种群的个体结构编码采用矩阵表示，它与神经网络某一模块的连接关系是一一对应的。有些特殊矩阵的某几行全为零，或者某几列全为零。在神经网络中，如果一个隐含层节点没有输入或者输出，这个节点是没有意义的，应该把这些没有意义的节点删除。删除了这些节点，与之相关的连接权值也一并被删除，进化子种群个体编码的长度将大大缩短，有效的降低了算法计算的复杂程度。因此，当计算某个进化子种群的个体适应度值时，应当首先检查其结构部分，若有全为0的行或列，应动态调整相应的个体的结构编码。例如当某个个体结构矩阵SP的第k行全为0，那么个体Sp+1的第k列也全为0；同样，当结构矩阵Sp的第k列全为0，个体Sp+1的第k行也全为0。当个体Sp+1结构部分编码发生变化以后，其连接权值部分编码也发生相应的变化，即应删除相应的实数编码。
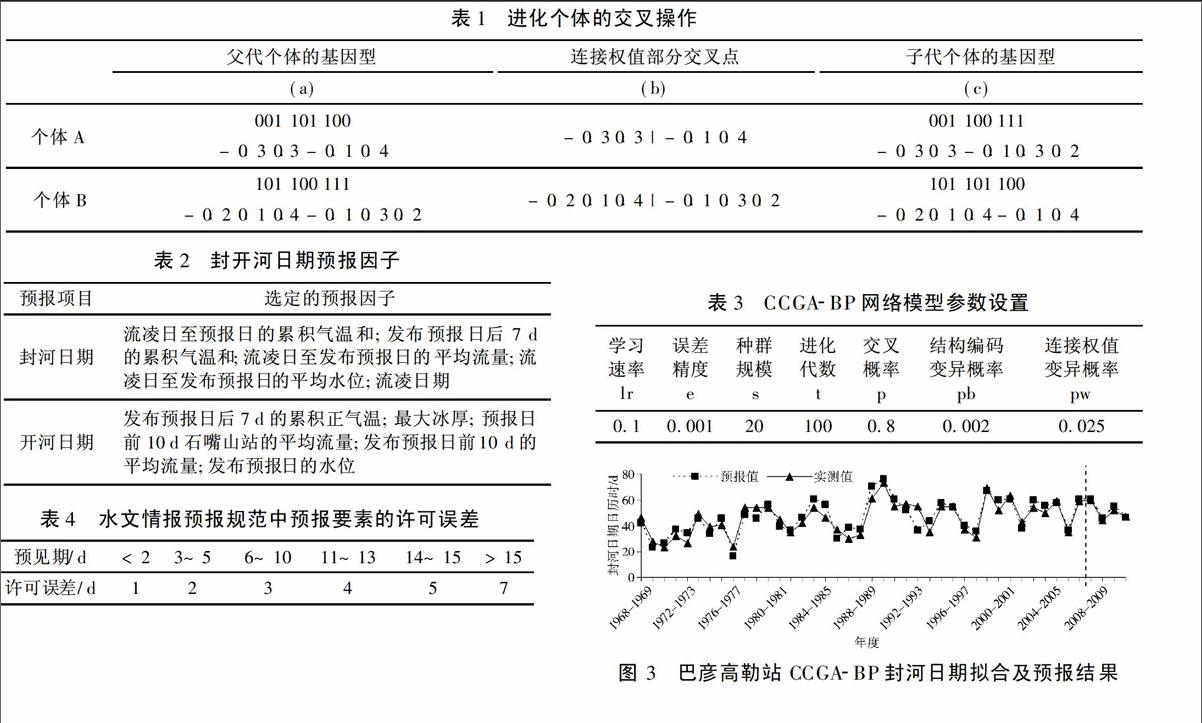
表1进化个体的交叉操作
父代个体的基因型
连接权值部分交叉点
子代个体的基因型
（a）（b）（c）
个体A001 101 100-03 03 -01 04-03 03 | -01 04001 100 111-03 03 -01 03 02
个体B101 100 111-02 01 04 -01 03 02-02 01 04 | -01 03 02101 101 100-02 01 04 -01 04
2应用实例
黄河宁蒙河段自宁夏的中卫县南长滩入境，流经宁夏、内蒙古河套平原。宁蒙河段处于黄河流域最北端。由于河道流向总体由低纬度流向高纬度地区，故流凌封冻由内蒙古河段下部溯源而上，解冻开河则从宁夏由上到下，河槽蓄水量逐段释放，开河最大流量逐渐增大。黄河河道较窄、流速较缓，极易形成凌灾[10]。宁蒙河段主要有石嘴山、巴彦高勒、三湖河口和头道拐4个水文观测站，本文根据这4个水文站的水情、冰情实测资料，建立冰凌预报模型并进行模型验证。
2.1确定预报因子
以往的研究表明[11-12]，影响冰情的主要因素有：（1）河流形态特征；（2）热能因子；（3）动能因子。由于河流形态特征影响复杂且相关资料难以获得，本文主要从热能因子及动能因子入手。太阳能辐射和地面反射决定大气温度，气温又密切影响着冰水温度。因此，气温是影响冰情变化的热能因子的集中表现，气温高低决定着冰量和冰晶凝结程度，是影响河道流凌、封河和开河日期的主要因子，因此可以用气温作为表征热能状况及其变化的基本因子。当水位平稳时，大部分冻冰就地消融，形成“文开河”的河势；而当水位快速上涨时，导致水鼓冰裂，从而形成“武开河”的河势。因此，可以用水位作为冰情演变的动能因子。此外，流量本身可以同时反映热能因子与动能因子，在水温相同时，流量越大，水体的储热量越多，且水流动力作用越大，在同样的气温条件下，河道里的水体越难结冰。经过以上分析，确定宁蒙河段封开河日期预报因子见表2。
表2封开河日期预报因子
预报项目选定的预报因子
封河日期流凌日至预报日的累积气温和；发布预报日后7 d的累积气温和；流凌日至发布预报日的平均流量；流凌日至发布预报日的平均水位；流凌日期
开河日期发布预报日后7 d的累积正气温；最大冰厚；预报日前10 d石嘴山站的平均流量；发布预报日前10 d的平均流量；发布预报日的水位
限于篇幅，本文仅以三湖河口站封河日期预报说明详细求解过程，其他站可做类似求解。
2.2巴彦高勒站封河日期预报
为计算方便，将封河日期转换为数字序列。以11月1日为基准点，例如巴彦高勒站多年平均封河日期为12月6号，记为36。根据巴彦高勒站实测冰情资料，对输入输出数据进行归一化处理。为检验模型的精度，将1969年-2006年序列样本用来训练模型，预留2007年-2011年5年的数据资料来检验模型预报精度。在模型训练中，将1969年-2011年纵向分割BP神经网络为2个进化子种群数，按照表3对模型参数进行设置，将5个预报因子作为输入，封河日期作为输出，隐含层节点数取初始值为3。独立运行CCGA-BP模型5次后，其优化过的网络隐含层节点数平均值为8个。
模型运行5次后，得到的网络输出平均值与封河日期实测值的拟合效果见图3。
表3CCGA-BP网络模型参数设置
学习速率lr误差精度e种群规模s进化代数t交叉概率p结构编码变异概率pb连接权值变异概率pw
0.10.001201000.80.0020.025
图3巴彦高勒站CCGA-BP封河日期拟合及预报结果
2.3模型效果评定
为检验模型的适用性，将其预报结果与PSO-BP神经网络模型的预报结果进行了对比。对预报结果进行取整，计算其预报误差，并根据《水文情报预报规范》判定模型的效果，见表4和表5。由表5可知，在巴彦高勒站的封河日期预报中，CCGA-BP模型的预报误差均在许可误差范围之内，合格率为100%，为甲等预报。而PSO-BP预报模型结合格率为80%，这是因为在2010年-2011年度的封河过程中，由于强冷空气的影响，河道出现流凌后迅速封冻，致使预见期过短，影响了预报模型的精度。
表4水文情报预报规范中预报要素的许可误差
预见期/d<23～56～1011～1314～15>15
许可误差/d123457
表5巴彦高勒站封河日期预报模型效果检验
3结论
（1）探讨了CCGA算法的原理，在分析封开河日期影响因素的基础上，选取合适预报因子，构建了CCGA-BP预报模型。将CCGA-BP预报模型应用到黄河宁蒙河段巴彦高勒站封河日期的预报中，结果表明，CCGA-BP模型历史样本拟合合格率达到893%，预报检验合格率为100%（5/5），模型可以用于冰凌预报实践。
（2）CCGA-BP模型有效克服了遗传算法不能进行网络结构和连接权值的同步优化，并且计算量大的缺点，其优化性能更高。实例应用结果表明。基于合作型协同进化遗传算法的BP神经网络模型应用于黄河宁蒙段冰凌预报是可行的。
参考文献：
[1]蔡琳.黄河防凌工作50年[J].人民黄河，1996，（12）：1-8.
[2]可素娟.黄河冰凌研究[M].郑州：黄河水利出版社，2002.
[3]茅泽育，吴剑疆，佘云童.河冰生消演变及其运动规律的研究进展[J].水力发电学报，2002，（1）：153-161.
[3]Edward P Foltyn，HungTaoShen.St.Law rence River Freeze-Up Fore-cast[J].Journal of Waterway.Port，Coastal and Ocean Engineering，1986，（4）：467-4811.
[4]Shen H T.Under cover transport and accumulation of frazil granules[J].Journal of Hydraulic Engineering，1995，（2）：184-1951.
[5]董雪娜，李雪梅，林银平，等.黄河下游凌情特征及变化[J].水科学进展，2008，19（6）：882-887.
[6]陈守煜，冀鸿兰.冰凌预报模糊优选神经网络BP方法[J].水利学报，2004，（6）：114-118.
[7]姚惠明，秦福兴，沈国昌，等.黄河宁蒙河段凌情特性研究[J].水科学进展，2007，18（6）：893-896.
[8]韩宇平，蔺冬，王富强，等.基于粒子群算法的神经网络在冰凌预报中的应用[J].水电能源科学，2012，30（3）：35-37.
[9]周翔南，王富强，蔺冬.基于遗传算法的SVM 冰凌预报模型研究[J].华北水利水电学院学报，2012，33（1）：19-22.
[10]王云璋，康玲玲，陈发中，等.近30a气温变化对黄河下游凌情影响分析[J].冰川冻土，2001，23（3）：323-327.
[11]蔡琳，卢杜田，蔡彬.水库防凌调度数学模型的研制与开发[J].冰川冻土，2002，24（2）：214-217.
[12]王志兴，李成振，范宝山，等.改进的遗传BP交叉训练算法及其在河流冰情预报中的应用[J].水力发电学报，2010，29（1）：76-80.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/1/3 18:45:08