《基于学生本位，聚焦高阶思维》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

基于学生本位，聚焦高阶思维

范文

何佳丹

【摘要】思维是数学学习的重要形式.提升数学核心素养的关键是聚焦高阶思维发展.要想发展学生的高阶思维，教师必须有效设计学习任务，立足学生本位，引导学生超越浅层、被动的学习状态，使学生展开深度性、批判性、探索性和创造性的自主学习.

【关键词】高阶思维;核心素养;有效设计;学生本位

一、高阶思维的重要意义

新课程背景下，教育教学提倡以“学科核心素养”为纲，关注学生未来长久发展的素养.数学作为促进学生全面发展的重要学科，一方面要使学生掌握现代生活和学习中所需要的数学知识与技能，另一方面要充分发挥数学在培养学生的科学推理和创新思维方面的功能.由此可见，数学学习离不开思维，思维是数学学习的重要形式，高阶思维又是思维的高级形式，因此提升数学核心素养的关键是聚焦高阶思维发展.高阶思维是指创新能力、问题求解能力、决策力和批判性思维能力.培养高阶思维能力，能有效促进数学核心素养的落实，提升数学核心能力.

二、从思维发展看当前课堂教学的现状

1.多

在日常的教学中，教师常受课堂教学时间的限制，为了更好地完成相应的教学内容，课堂中常出现教师讲授多、学生表达少的现象或个别师生交流多、全体师生互动少的现象，教师或少数学生的想法代替了全体学生的思维，学生思维多元化发展受限.

2.快

课堂教学进度快是当前数学教学中存在的常见现象.学生刚接收一个新的知识，还未来得及好好消化咀嚼，紧接着快速转换到下一环节进行更具挑战的任务.学生没能获得充足的探究、思考、分析的时间与空间，容易出现知识链的脱节和错乱.

3.低

探究性学习已经成为当下课堂教学的主流方式.教学中常常看到教师组织学生开展探究性学习任务.在实际活动过程中，多数学生是被教师牵引着被动完成相应任务的，学生缺乏独立思考、主动探索和批判质疑的精神.这样的活动仅仅停留在低阶思维水平，思维含量低，课堂效率低.

4.少

上述低阶思维学习活动的发生，其实是教师缺少高阶思维培养意识.学生只获得对知识的记忆和基本理解，至于独立发现问题、提出问题、解决问题的能力以及批判、质疑和创新精神，都无法达到.

三、教学实践：例谈培养高阶思维的具体路径

教师和学生共同期待、向往的数学课堂应该是注重高阶思维发展，真正关注学习过程体验的课堂.笔者以人教版六上的“方与圆”练习课为例进行教学，突破常规教学模式，在课堂中聚焦学生高阶思维的培养，取得了较好的效果.

（一）有效设计学习任务，指向高阶思维发展

为了使数学学习指向高阶思维发展，教师需要重组学习内容和结构，精心设计实施教学方案，为培养学生分析、评价、创造三方面的思维能力发展提供充足的空间.

1.开放式素材，培养发散性思维

【教学案例片段1】

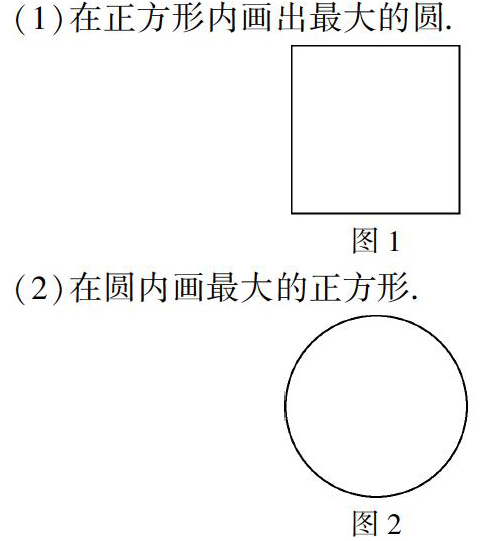
笔者设计了以下两幅图，作为“方与圆”练习课的前测作业，请学生按要求画一画.

（1）在正方形内画出最大的圆.

（2）在圆内画最大的正方形.

图上没有任何数据提示，学生需要自己探寻，想办法通过测量获得所需要的数据并画出图形.在对材料信息的处理中，学生各显身手，唤起对新课中方与圆的知识的回忆，彰显个性思维.

【教学案例片段2】

活动探究：我们先来研究图1这样的方中圆组合图形.请利用你手中的组合图形，算一算正方形和圆的面积比是多少？

组合图形中没有数据且大小不同的开放材料的设计恰到好处，教师可以从研究中观察学生的多元思维.学生运用已有的知识基础和学习经验，自行分析现有的和隐含的学习素材，选择适当的素材.有的学生通过测量数据来进行推导，有的学生不使用具体数据，利用假设法展开推理，即假设半径是一个具体数，或者用字母r来推算.这些开放式素材的投放，受众面广，对不同学生都发挥价值，引发不同思维水平的学生进行深度学习.学生在尝试中及時有效地触发其知识、能力的成长，从一种思维到多元思维，使发散性思维得到培养.

2.大任务驱动，激发高阶思维萌芽

【教学案例片段3】

师：我们继续来研究圆中方组合图形，猜猜看此时正方形和圆的面积还会存在一定的规律吗？

生：会.

师：你打算怎么研究？（静静等待2分钟）

交流方法：

生1[]和研究方中圆一样，先量出圆的半径，计算面积，再算出正方形的面积，最后求面积比

生2[]要多选几个数据，用不同数据计算，才能发现规律

生3[]用字母r来表示圆的半径，计算出正方形和圆的面积

生4[]用字母a表示正方形的边长，计算出正方形和圆的面积

优化：你们认为哪名同学的方法更有效？说一说理由.

生5：一个个数据计算太麻烦了，用字母表示数，包括了可能的所有数据，结论更具有一般规律性.

实践：学生尝试用字母r表示圆的半径，展开计算和推理.

反馈：S正∶S圆=2r2∶πr2=2∶π.

发现：通过具体数据的计算，我们发现圆中方组合图形中正方形和圆的面积比总是2∶π.

此处教师设计大任务框架，留白空间，没有给定提示语和操作步骤等限制，以此激活个体创造性思维，引发学生的多向交流.学生不受按部就班的研究方法和学习步骤的框定，思维就会非常活跃，能够唤醒内在已有的知识和学习经验，尝试寻找有效策略解决问题，多元化思维得以呈现.在大任务驱动下，学生的思维正在逐渐进阶，从一类到多类，从特殊到一般，学生的认知也趋于完整、深刻.随后，教师以恰当而富有启发性的问题“哪种方法更有效？说一说理由”启发学生展开深度思考，不断调整思维.于是，教师在探寻研究方法中，进一步达成一致优化策略解决问题，即用字母表示数来研究最有效，从而形成对这类知识的本质认识，发展学生的高阶思维.

（二）立足学生本位，组织促进高阶思维的学习活动

数学学习活动的高阶思维训练必须坚守学生本位、學生立场.高阶思维重视学生主体的自觉自悟，致力于数学素养的落实.

1.沉淀个体思考，尊重个性化思维

（1）自主探究，彰显个性化思维，激发创造性思维

高阶思维产生于高质量的个体独立学习.教学案例片段3的研究学习活动中，教师给予学生充足的时间和空间展开自主学习，独立思考.学生主动经历猜测、观察、思考、比较、归纳、实践、计算、推理等活动，寻找解决问题的策略和方法.在学生个性化的思维得到彰显后，该研究活动就有多个思考角度、多种解决方法，我们可在异中求同、求佳.此刻，学生的学习不再是停留在表层，也不是被动的状态，而是展开了深度的探索性学习.在沉思冥想中，学生的创造性思维得到激发，解决问题的数学核心能力真正得以提升.

（2）长时间思考，发展思维的深刻性和全面性

数学学习也需要有静谧的时光，教师需要在教学过程中适度留白，给学生留有独立思考的空间与时间，这样才会有高阶思维活动参与进来.

【教学案例片段4】

①下图整个图形与阴影部分的面积比是多少？

②下图是一个半圆，三角形和半圆的面积比是（?）.

③下图中阴影部分的面积是4 cm2，求圆的面积.

通过对方中圆和圆中方组合图形的加工和改造，教师设计了三道变式练习.习题①是方中圆扩大2倍的结果，习题②是圆中方缩小为原来的二分之一，习题③是圆中方的更高阶变式.三道习题思维梯度高，具有一定挑战性.此类问题要求高，要给学生较长的时间进行充足的思考、分析和解答.长时间思考难题，使学生的思维发生触动，唤起对前后知识之间的关联;寻找知识的脉络，发现来源是圆中方或方中圆基础图形;在变中抓不变，应用于变式题中，最后解决问题.长时间的思考，使学生开启了深度学习的大门.学生经历了个体独立思考的操作过程，对问题的解决有了自己的体验与想法.在长时间的思考过程中，学生的思维深度参与且变得全面和深刻，挑战了高阶思维，问题解决能力也相应得到提升.

2.分享集体经验，促进思维拓展

课堂教学既要关注个体发展，也要面向全体，鼓励全员共同参与，形成学习共同体，展开师生互动和生生交流.集体经验和方法分享的形式让不同观点和思维得到充分尊重和重视，使学生能更好地理清自身的逻辑思维，提升语言表达能力，发现解决问题的有效策略.

在方中圆组合图形面积关系的研究环节中，学生基于独立思考后，再进行精彩的经验分享.学生在多种方法辩论中进行思辨，经历质疑、讨论、批判和关联，最终明确用字母表示数获得的结果更具一般结论性，且更加高效.练习环节，在学生完成后，教师组织学生说一说各自的想法.习题③是圆中方的更高阶变式，对学生来说更具挑战，是发展高阶思维的关键处.教师可以在与学生交流中看到每种方法背后学生的知识基础和思维水平.有学生对图形的面积公式十分熟练，利用三角形面积公式求出r2，进一步通过圆的面积公式求解圆面积.也有学生则是学会了应用本节课圆中方的知识，自主解决问题，即将图形补充还原成圆中方，由三角形面积推导出正方形面积，再借方与圆的面积关系，通过份数计算出每一份的大小，最后算出圆的面积.这两种方法均体现出学生已经较好地掌握了本课的新知，并能够自主运用解决相关的问题.学生的思维和能力都得到一定发展.学生不需要将图形还原成完整的圆中方，仅在四分之一圆中方中依旧可以运用2∶π的面积关系推算四分之一圆的面积，最后回归到求整圆面积.

在有效的集体互动中，学生分享交流的内容更趋于全面和深刻，学生在倾听中获得了更多的思考，拓宽了对本题相关知识和方法的认知领域，促进了思维品质的提升与拓展.

四、结束语

随着课堂教学的不断优化和发展，增强运用高阶思维指导教学活动是每位教师都应该探索和努力的方向.数学学习不是简单地把知识塞进学生的头脑中，而是让学生的思维活跃.教学的最终指向是关注学生的长远学习，让学生学会思考、学会质疑、学会分析、学会创新，获得学习的方法和思考的模式.要想发展学生的学习能力，落实核心素养，就必须重视培养学生的高阶思维.

【参考文献】

[1]王莹.“高阶思维”与学生数学“深度学习”[J].数学教学讯，2018（19）：13-14.

[2]程明喜.小学数学“深度学习”教学策略研究[J].数学教育学报，2019，28（4）：66-70.

[3]袁爱国.高阶思维与语文深度学习[J].教育研究与评论（中学教育教学），2017（11）：5-11.

[4]冯幼绒，孙天山.基于问题的高阶思维教学研究[J].化学教与学，2016 （5）：2-4.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。