《基于排队论的合成营单独执行任务某类装备保障单元需求测算》-工学论文，工程论文-论文范文参考-科学狗论文网

标题

基于排队论的合成营单独执行任务某类装备保障单元需求测算

范文

王学智

摘要：本文运用排队论中单服务台等待制排队系统和多服务台混合制等待排队系统，通过问题描述、模型建立、定性分析和示例分析，以某类装备保障单元为测算对象，测算了合成营单独执行任务时某类装备保障单元数量需求，为合成营单独执行任务装备保障力量需求提供了一种定量分析的方法。通过定性与定量分析相结合，不断提升装备精确保障水平。

Abstract： In this paper， in order to solve the problem of the requirements of some equipment support unit for Synthetic Battalion to perform tasks alone， the single service tamping waiting system and the multi-service ramming platform mixed waiting queuing system are used in the queuing theory， by problem drawing， model establishment， qualitative analysis and example analysis， a certain kind of equipment support unit is taken as the measering object. This paper provides a quantilative analysis method for the equipmen support force demand of the Synthetic Battalion to carry out the task alone. Through the combination of qualitative and quantitative analysis， continue to improve the level of accruate equipment support.

关键词：排队论;保障单元;测算

Key words： queuing theory;equipment support unit;forecast

中图分类号：E257 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文献标识码：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編号：1006-4311（2019）20-0065-04

0 ?引言

组建合成旅后，合成营作为合成旅的战斗主体，装备种类、数量较以往有了大幅提高，装备保障任务繁重，组织指挥复杂，对装备保障力量提出了更加严格的要求。未来合成营极有可能单独赴某一方向执行作战或非战任务。因此，保障机关需要根据装备保障任务测算保障单元需求，为合成营单独执行任务提供精准的装备保障，为实现作战效益的最大化提供重要支撑。

1 ?问题描述

装备保障单元是由执行某项装备保障任务所需的最小的保障人员、必需的保障装备等组合成的一个要素齐全、功能匹配的保障集合体[1]。保障单元具备独立的保障功能，可独立遂行特定任务。不同类型的保障单元对应装备的不同部件故障，如履带装备底盘维修单元对应维修的是履带装备底盘故障，轮式车辆底盘维修单元对应维修轮式车辆底盘。保障单元是装备保障力量的基本组成单位，只要测算出保障单元的需求，就可以确定保障人员、保障装备、器材、设备等要素的需求，进而确定整个保障模块的需求。在执行装备保障任务过程中，也是以保障单元为单位，这里我们把每个保障单元看成是一个服务机构，装备发生故障后需要到服务机构去排除故障，为尽快恢复战斗力，故障装备应及时得到修复，达到上级要求的装备完好率。若需要排队等待，则等待时间越短越好，这就需要我们测算到底需要多少保障单元才能达到上级规定的装备完好率指标。

2 ?建立模型

2.1 系统假设

以某类装备保障单元负责维修故障装备某类部位为研究对象，将某单独执行任务的合成营发生的故障装备看成是故障装备抢修排队系统的“顾客”，合成营执行任务时集中配置，保障单元定点保障，先从最简单的情况开始研究，即只有一个保障单元的情况下看是否能够达到上级要求的装备完好率，如果一个保障单元不能满足要求，那就要增加保障单元的数量。每个保障单元同一时间内只能保障1台装备的维修工作，装备因故障而进入待修状态，并使待修的装备形成队列，每台有故障的装备到来并经过抢修后仍回到原来的总体，所以仍可以再次到来，这样就可以构成一个排队系统，如图1所示。

为了便于建立故障装备抢修排队系统模型，对故障装备到达过程、排队规则、服务规则等情况进行如下假设：

①到达过程。装备发生故障具有如下规律：一是某合成营单独执行任务时，力量集中使用，装备集中配置，每台装备单位运转时间内发生故障的平均次数是相同的;二是设t为执行任务中的某一时刻，对于一个足够小的时间间隔？驻t，在任意t+？驻t时间段内产生一台故障装备的概率与t是无关的，这些概率都是常数。三是装备一旦发生故障立即送到保障单元所在的位置进行维修。上述规律符合泊松（Poisson）分布的特征。

②排队规则。故障装备会根据装备故障发生的规律源源不断到来，由此所产生的排队规则是等待制，保障单元空闲时就抢修，无空闲时故障装备就进入排队系统等待。排队系统中的服务机构只有1个保障单元时，故障装备按照到来的顺序进行排队，排队系统中有2个或2个以上的保障单元时，故障装备到来，优先选择空闲的保障单元，在排队等待维修的过程中，如果某个保障单元出现空闲，可以离开原来的队列而进入到空闲的保障单元进行维修。

③服务时间。假设平均每次每台装备完成抢修的时间为μ，修理时间都服从参数为μ的负指数分布;

④保障单元具有连续工作的能力，不会发生人员、保障装备的战损，且维修器材持续供应;

⑤装备的平均故障率用λ表示，各个部件的平均故障率是不同的，如底盘和上装部分的故障率是不同的，在测算分析时，要根据不同的保障单元来确定。该项数据可由平时维修的经验数据得出。

通过以上系统假设和分析，故障装备维修排队系统的输入过程为泊松过程。此过程我们可以用排队系统的状态转移速度图表示，见图2。

λ代表的是故障装备进入系统的速度，μ是输出修复装备的速度，随着服务台数量即保障单元数量的增加，输出速度增大，当服务台增大到一定数量时，输出速度不再增大，此时如果再增加保障单元的数量，就会造成资源的严重浪费。

2.2 模型建立

通过以上设定和分析，解决此类需求测算问题我们可以采用排队论的方法，在测算过程中，我们需要分别对不同的保障单元进行测算，这里选取其中常用的一种类型的保障单元为例，先从最简单的情况入手，运用排队论中最简单的M/M/1排队模型解决此类问题[2]。

2.2.1 建立M/M/1排隊模型

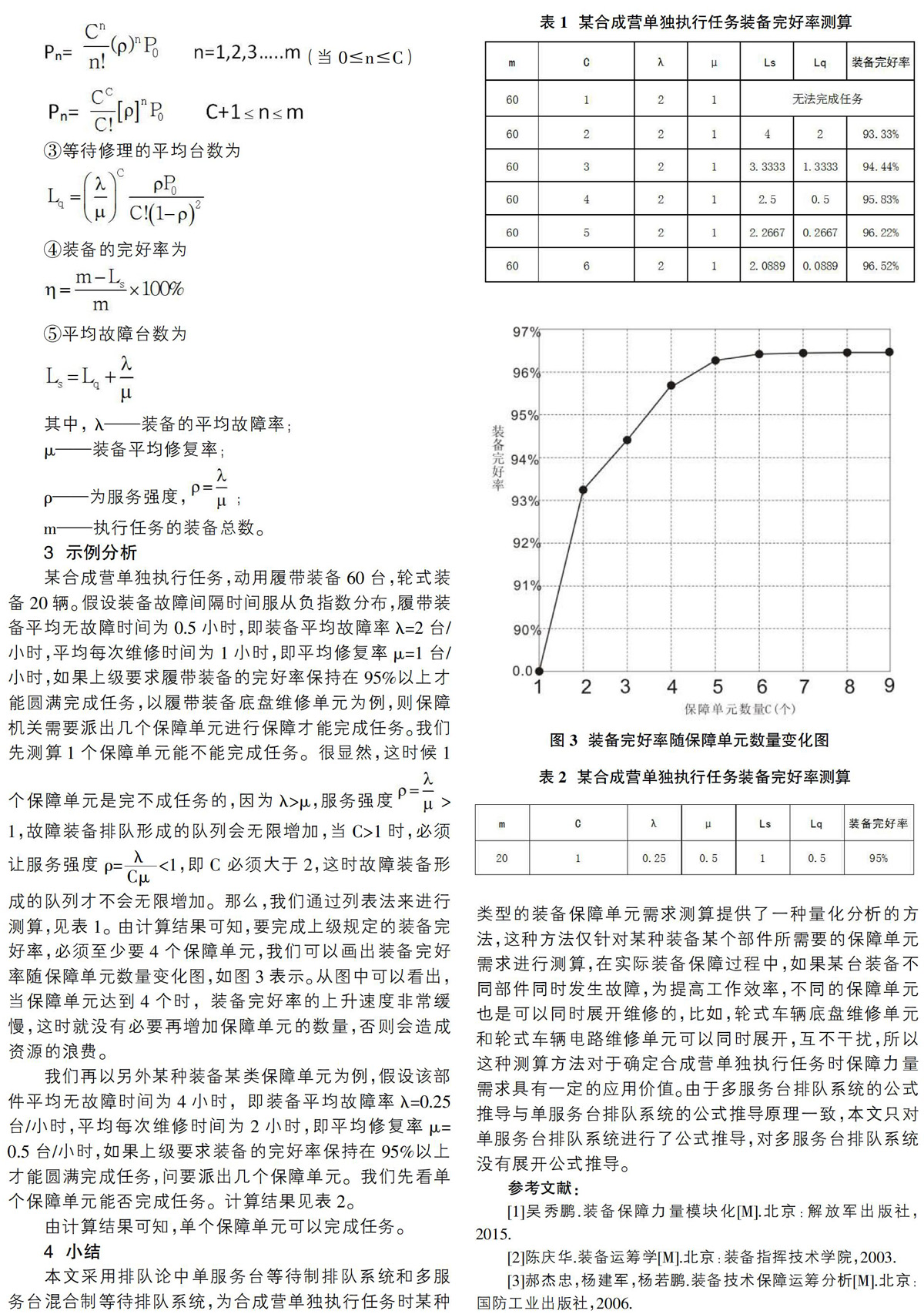
我们再以另外某种装备某类保障单元为例，假设该部件平均无故障时间为4小时，即装备平均故障率λ=0.25台/小时，平均每次维修时间为2小时，即平均修复率μ=0.5台/小时，如果上级要求装备的完好率保持在95%以上才能圆满完成任务，问要派出几个保障单元。我们先看单个保障单元能否完成任务。计算结果见表2。

由计算结果可知，单个保障单元可以完成任务。

4 ?小结

本文采用排队论中单服务台等待制排队系统和多服务台混合制等待排队系统，为合成营单独执行任务时某种类型的装备保障单元需求测算提供了一种量化分析的方法，这种方法仅针对某种装备某个部件所需要的保障单元需求进行测算，在实际装备保障过程中，如果某台装备不同部件同时发生故障，为提高工作效率，不同的保障单元也是可以同时展开维修的，比如，轮式车辆底盘维修单元和轮式车辆电路维修单元可以同时展开，互不干扰，所以这种测算方法对于确定合成营单独执行任务时保障力量需求具有一定的应用价值。由于多服务台排队系统的公式推导与单服务台排队系统的公式推导原理一致，本文只对单服务台排队系统进行了公式推导，对多服务台排队系统没有展开公式推导。

参考文献：

[1]吴秀鹏.装备保障力量模块化[M].北京：解放军出版社，2015.

[2]陈庆华.装备运筹学[M].北京：装备指挥技术学院，2003.

[3]郝杰忠，杨建军，杨若鹏.装备技术保障运筹分析[M].北京：国防工业出版社，2006.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。