网站首页  词典首页

请输入您要查询的论文：

　

标题 “先学后教，合作分享”塑造课堂新生态
范文 徐玉平

[摘 要] 课堂教学必须以学生的“学”为中心，“教”以“学”而定；课堂是师生、生生基于平等民主氛围下多向的“对话场”，在对话中追求人与人之间的沟通、理解和创新.
[关键词] 小学数学；课堂教学；先学后教；合作分享
■ 课堂随思
“量角的大小”是一节操作技能课，按传统教学观来看，无非是教会学生用量角器量角的方法，再通过反复操作让学生掌握技巧，熟练度量. 可实践中师生往往搞得焦头烂额，效果还是差强人意. 究其原因，教师只教学生怎么量，没有引导学生思考“为什么这样量”. 课堂上只有技能的操作，没有数学思想的领悟、数学经验的积累，这是一种缺乏数学教育价值的教学. 特级教师华应龙曾对“量角的大小”一课进行过精彩演绎，他提出，“量角的本质就是量角器上的角与所量角的重合”，由此，我深受启发：这节课可以围绕量角的本质主要研讨三个问题，即“量角器的构造”“怎样用它量角”“量角时要注意什么”. 课堂教学由量角技能的传授转向量角本质的探索，注重学生基本数学经验的积累、数学思想方法的领悟，让一节操作技能课也有浓浓的“数学味”.
■ 课堂剪影
片断一：复习引入
呈现图形——角.
师：关于角，大家已经知道了些什么？
生1：由一点引出两条射线组成一个角. 这个点就是角的顶点，两条射线就是角的两条边.
生2：角的大小跟两条边张口的大小有关，跟两边的长短无关.
生3：角有锐角、钝角，还有直角.
师：角是有大小的，这个角有多大，可以用什么来量？
生4：用量角器.
师：量角器是专门量角的工具，这节课我们一起学习怎么用量角器量角的大小. 这节课我们主要研究三个问题，即量角器上有些什么？怎么用它量角？量角时要注意什么？最后，咱们搞一份量角器的使用说明出来，好不好？
片断二：认识量角器
1. 认识内、外圈刻度和刻度线
师：观察量角器上面有些什么，把你的发现在小组里说一说.
生1：量角器是半圆形的，上面有0，10，
20…直到180的数，有两圈这样的数.
生2：两圈数排的方向是反的，外圈的数是顺时针方向排的，里圈的数是逆时针方向排的.
生3：这些数都表示角的度数，0就是0°，10就是10°.
师（追问）：度数是什么？
生4：度数是表示角的大小的.
师：“度”是表示角大小的计量单位. 外圈的度数就叫外圈刻度，那内圈的度数呢？
生（齐）：内圈刻度.
师：还有什么发现么？
生5：量角器上有很多刻度线，都对着量角器的中心.
生6：刻度线的一头对着中心，另一头对着内、外圈两个刻度.
师：刻度线对着哪个刻度，就叫多少度刻度线. 同学们在自己的量角器上先找到中心，再顺着中心往外任意找一条刻度线，并读一读.
2. 找角
（1）找标有度数的角，初步体会内、外圈刻度的读法
师：量角器上除了这些，还有什么吗？
生1：还有角！把两条刻度线合起来看就组成角.
师：大家仔细找一找，能发现多少度的角呢？
生2：我找到了90°角. 顶点是量角器的中心，一条边是90°刻度线，另一条边是0°刻度线.
师（追问）：为什么是90°呢？
生2：因为一条边是90°刻度线，角自然就是90°了.
生3：我要补充一下，不能光看一条边，还要看另一条边，另一条边指着0°，角才是90°呢！
师：你补充得非常关键！量角器上角的起点是0°，所以要以0°刻度线为角的一条边，再以90°刻度线为另一条边，构成的角才是90°！我们旋转角的一边，看看它形成的过程.（演示：两条边都对准起点，一条边绕着中心旋转，从0°转到180°）
生报出屏幕上由小到大出现的角的度数.
师：刚才我们读角的度数，读的是哪圈刻度？为什么？
生4：从外圈的0°开始数的，角的度数要读外圈的刻度.
师：还有90°角么？
生5：以0°刻度线为角的一边，另一边对准90°刻度线，就是90°角.
师：如果继续旋转角的一边，会出现哪些度数的角呢？请你演示，我们来读.
师：刚刚我们读的又是哪圈刻度？为什么？
生6：我们读的是内圈刻度，因为是从内圈0°开始数起的.
师：回顾两次读角的度数，你有什么发现？
生7：要想读正确角的度数，要先看看0°在哪儿.
生8：如果从内圈0°数起，就读内圈刻度；如果从外圈0°数起，就读外圈刻度.
师：同学们发现了0°刻度线是量角器上非常重要的刻度线，它在哪里角的起点就在哪里.
（2）找没标出度数的角，体会统一度量单位的意义
师：能找到没标出度数的角么？
生1：我找到了43°角，它比40°多出了3小格，就是多出了3°，所以是43°.
生2：我还知道量角器上一小格对的角就是1°的角.
师：人们在实践中发现，只要度量就需要统一单位，量角也不例外. 于是规定：把半圆分成180等份，每一份所对的都是1°的角，1°角的大小是确定不变的. 一个角有多大，就可以用“多少度”准确地表示出来.
（3）找任意度数的角，整体感知量角器的构造
师：量角器上的角可多了，从1°到180°全都有！你可以找任意度数的角，这样的角能找到两个么？同桌互相指指说说.
片断三：探索量角的方法和本质
师：认识了量角器的构造，接下来可以研究……
生（齐）：怎么用量角器量角.
师：为方便大家研究， 老师提供几点提示——（1）试着用量角器量出角的度数；（2）归纳一下量角的步骤；（3）想想为什么这样量.
生先独立研究，然后小组讨论，全班交流.
生1演示量角的过程.
师：谁来回顾一下她量角的步骤？
生2：先把量角器的中心对准角的顶点，然后把0°刻度线对准角的一条边，再看到另一条边对准的是60°刻度线，这个角是60°.
生3（犹豫地）：我觉得是……120°吧.
生4（急切地）：你把刻度看错了，你要先看看0°在哪儿，是内圈还是外圈.
生3：哦！应该读内圈的刻度，因为0°在内圈！
师：为什么这样操作就能确定量的角是60°呢？
全班陷入沉思，小组自发议论起来.
生5（惊喜地跑到屏幕前）：我们组发现，量角器上这个位置有个60°的角，它和要量的角重合在一起了，所以这个角就是60°！
生（恍然大悟）：哦，原来是这样……
师：从量这个60°角中大家有没有受到启发？为什么用量角器可以量出角的度数？它上面不同度数的角有什么重要作用？
生6：我们只要把量角器上的角和要量的角重合，量角器上的角是多少度，要量的角就是多少度.
师：同学们真厉害，你们发现了量角的秘密——角与角的重合！怎么才能让量角器上的角与要量的角重合呢？
生7：先把量角器的中心与角的顶点重合，再把0°刻度线和角的一条边重合，最后看另一条边对准的是多少度刻度线，这个角就是多少度.
师：要量得准，就要重合得准. 现在量角你有信心吗？
片断四：巩固方法，明晰内、外圈刻度的读法
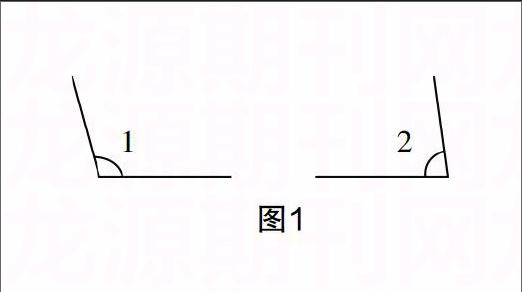
1. 量出下面各角的度数.？摇？摇？摇
■
生独立量角，小组互相交流纠错.
生演示量角过程.
师：我们读这两个角的度数时，为什么∠1要读内圈刻度，∠2要读外圈刻度？
生1：因为∠1一条边对的是内圈0°，所以顺着内圈依次读；∠2一边对着外圈0°，那就要顺着外圈读.
2. 判断下面量角的方法是否正确，怎样修正？
生观察纠错.
师：量角的时候要注意什么？把你的经验跟大家分享一下.
生1：要把中心和顶点完全重合，0°刻度线和一边完全重合，要重合得很准！
生2：我要提醒大家，读刻度时，要先看好0°在哪里，顺着0°去读，不要把内外圈读反了.
3. 生活中的量角
师：学会量角在生活中很有用. 我们如东是有名的风筝之乡，这是举办的国际风筝节，哪个风筝飞得最高？（出示“你知道么”，介绍比角的方法）
师：滑梯斜面跟地面之间形成一个角，多少度比较合适呢？学生桌椅的椅背微微倾斜，跟椅面之间也构成一个角，多少度最好呢？
生测量汇报.
片断五：总结回顾，编量角器使用说明
师：这节课快要结束了，量角器使用说明可不可以新鲜出炉了？
生围绕课伊始提出的三个主要问题进行总结.
■ 课堂解读
1. 以“先学后教、合作分享”为主要学习方式，促进学生自主探索、多向交流
课堂教学必须以学生的“学”为中心，“教”以“学”而定；课堂是师生、生生基于平等民主氛围下多向的“对话场”，在对话中追求人与人之间的沟通、理解和创新. 在这样的教学理念下，“先学后教、合作分享”的学习方式应成为课堂教学的“主旋律”，塑造“以人为本”的新生态. 本节课，学生围绕三个问题展开探索，都是个人自学为先，小组合作为主，全班交流为平台，每位同学都卷入了对话，经历了释疑、补充、梳理、概括等过程. 以“怎样用量角器量角”的探讨为例，学生根据研究提示，有序地展开了自主探索与合作. 在全班交流环节，师生围绕研究提示展开多向对话：“谁能回顾一下这位同学量角的步骤”“我认为这个角的一边对准的是60°刻度线，角是60°” ；“我觉得这个角是120°”. “我提醒你看一看0°的位置，在内圈还是外圈”“哦！是我看错了”，在生生互相质疑的补充中，怎样读刻度的问题得以明晰. “为什么这样量就能确定角是60°”“量角器量角的秘密是什么”，学生又陷入沉思，有小组率先发现：“我们发现量角器上60°角与要量的角重合了，所以这个角就是60°. ” “ 哦，原来是这样！”全班学生豁然开朗——“只要把量角器上的角与要量的角重合，角的度数就有了. ”学生时而争论、时而沉思、时而顿悟，经历了丰富的对话与思考过程，对量角方法不仅知其然，更知其所以然，凸显了数学教学的价值.
2. 以“大问题解决”为教学结构，释放更多空间给学生展开对话与思辨
学习方式的转变必须以教学结构的改革为前提. 以往那种环环相扣、行云流水式的课堂，学生被教师刻意拆分出来的小问题牵着鼻子走，难以有充分的思考和交流时间，说到底，还是“师本”课堂. 要想变成以学生为中心的课堂，就必须把更多的时间让给学生. 抓住课眼，设计“大问题”使这一想法得以实现. 本节课，教师围绕量角的本质，删繁就简，提炼出三个主要问题：量角器上有些什么？怎样用量角器量角？量角时要注意什么？课伊始就进入问题情境，学生围绕这些问题逐一展开探讨，目标明确，层次鲜明. 这样的板块式教学，既扣住了大框架，又不拘泥于细节，把学生推到前台，为学生的先学、互学留足了空间，这样，学生展开充分的思考与对话才成为可能. “量角器的构造”——从认识内外圈刻度、刻度线，再到找角，学生自主观察，互为补充；“怎样用量角器量角”——学生尝试操作，总结方法. 在直观比较中感知重合，在合情推理中领悟本质；“量角时要注意什么”——前有孕伏，后有纠错，学生对这一问题的回答水到渠成；最后，“量角器的使用说明是不是可以新鲜出炉了”——围绕上述三个问题进行梳理与回顾，代替传统的课堂总结，前后呼应. 学生在解决问题的过程中个性思维得到了尊重与释放，学生体验到了合作分享的快乐.
3. 以“经历丰富的数学活动过程”为导向，促进“四基”目标整体达成
无论是学习方式的转变，还是教学结构的改革，都是为实现教学目标服务的. 2011版的新课标提出，让学生“获得适应社会生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验”. “量角的大小”这样一堂典型的操作技能课，应把重点由“教会学生量角的方法”转变为让学生“经历丰富的数学活动过程”，在过程中感知基本数学思想方法，积累基本数学活动经验，目标由“双基”变为“四基”. 纵观这节课，学生围绕主要问题进行的探讨活动贯穿始终，在活动中学，在活动中悟；不仅学会了量角、读角的方法，更领悟了为什么这样量. 这种从源头处习得的知识才能内化为知识结构，历久弥新；课堂上，有多次观察与操作活动，教学没有仅停留在得到活动结果，而是在此基础上，引导学生作进一步回顾反思：“回顾刚才两次读角的度数，你有什么发现”“她是怎样量角的？为什么可以这样量”“量角的过程中要注意什么”，鼓励学生把获得的经验与大家分享，最后，在解决实际问题时验证之前获得的经验，重新领悟并创造出新的经验. 数学活动经验就是这样在不断循环往复的过程中得以积累的.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 18:16:00