《基于遗传算法的超疏水冷凝表面结构优化》-工学论文，工程论文-论文范文参考-科学狗论文网

标题

基于遗传算法的超疏水冷凝表面结构优化

范文

龙绮睿

摘要：滴状冷凝是一种高效冷凝过程，是增强冷凝传热的重要措施。近年来发现滴状冷凝中弹跳凝结具有更高的换热系数，从而得到世界学者的关注。本文研究超疏水表面的弹跳凝结换热模型，并且基于遗传算法对超疏水表面结构进行换热优化。研究表面结构不同特征尺寸对换热性能的影响，得到一定条件下的最优表面结构特征。

Abstract： Dropwise condensation is an efficient condensation process and an important measure to enhance condensation heat transfer. In recent years， it has been found that bouncing condensation in droplet condensation has a higher heat transfer coefficient， which has attracted the attention of scholars around the world. This paper studies the bounce condensation heat transfer model of super-hydrophobic surface， and optimizes the heat transfer of super-hydrophobic surface structure based on genetic algorithm. The effect of different feature sizes of the surface structure on the heat transfer performance is studied， and the optimal surface structure characteristics are obtained under certain conditions.

關键词：超疏水表面;弹跳凝结;热阻分析;遗传算法

Key words： superhydrophobic surface;bounce condensation;thermal resistance analysis;genetic algorithm

中图分类号：O647.1 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文献标识码：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章编号：1006-4311（2020）01-0229-04

0 ?引言

与传统膜状凝结相比，滴状凝结具有更高的换热能力，吸引了世界学者的广泛关注[1]。近年来，弹跳冷凝现象被发现[2]，弹跳冷凝换热系数比传统滴状凝结的换热系数高出30%左右[3]。弹跳冷凝中的液滴在冷凝面上具有较高的接触角，并且发生合并后表面能释放使其自身发生自发弹跳[4]。与传统滴状凝结一样，弹跳冷凝的换热模型得到相应的关注。Kim[5]等人采用人口平衡模型来确定小液滴的动态平衡尺寸分布，大液滴采用Rose半经验幂函数[1]的尺寸分布，同时结合单液滴换热模型。Miljkovic[6]等人采用与Kim相似的换热模型，对于单液滴换热和小液滴尺寸分布考虑到液滴变接触角的影响，讨论了冷凝表面尺寸参数对液滴换热的影响。Zhang[7]等人根据液滴之间合并概率的关系建立适用于弹跳冷凝的尺寸分布模型，结合Kim等人的单液滴换热模型的综合换热模型，与实验数据相比模型准确性更高。

根据换热模型可以优化尺寸结构[6]，但是对于结构复杂一些的冷凝表面，如双亲表面[8]，分层表面[9]，仅使用换热模型很难得到较为准确的优化结果。Miljkovic[6]等人展示冷凝表面纳米柱和纳米柱半径对于冷凝表面换热具有较大影响。本文基于遗传算法方法结合弹跳凝结换热模型对纳米结构冷凝表面进行优化。建立了适用于纳米结构的优化模型，考虑到弹跳凝结现象和纳米结构对弹跳凝结换热的影响，最后揭示了超疏水表面结构参数对冷凝换热的作用和遗传算法控制参数对于优化结果的影响。

1 ?模型建立

1.1 超疏水表面弹跳凝结换热模型

本文建立超疏水表面弹跳凝结换热模型，以优化超疏水表面结构参数，从而达到最大换热系数的目标。弹跳凝结换热模型由单液滴热阻模型及液滴尺寸分布模型构成。其中，单液滴热阻模型是描述单个液滴在稳定凝结状态下的换热量[5]。单液滴换热量与相应液滴数量可以得到整个表面的换热系数。考虑到滴状凝结的特征，液滴数量存在区别大液滴与小液滴的尺寸参数，即液滴合并半径re=1/4■。液滴合并半径表示液滴生长到相应尺寸会发生合并现象，由于液滴在冷凝表面上是柏松分布[6]，所以合并半径是一个统计值。

1.1.1 单液滴热阻模型

1.2 遗传算法模型

遗传算法发展自生物进化理论，从生物进化角度去阐述优势放大的过程，遗传算法在求解全局最优解的情况下具有鲁棒性强的特点[10]。本文对超疏水表面结构进行研究，以求得在特定条件下的最优结构参数达到换热量最大的目标。

1.2.1 目标函数

遗传算法所采取的目标函数为优化超疏水表面换热能力，即目标函数为式（7），F=q。采取的优化对象为液滴之间的合并尺寸re和纳米柱直径d，同时为了方便讨论，对优化目标进行相应变换得到re/l和d/l。并且在进行计算中，对优化对象采用实数编码。

1.2.2 遗传操作

1.3 算法流程及模拟参数设置

本文利用MATLAB 2018Rb环境，对超疏水表面结构参数进行优化。具体建模过程如下：①初始化：对染色体进行初始化，采用实数编码;②适应度计算：根据相应的染色体计算整个表面的换热能力;③选择过程：对相应的染色体根据其适应度值进行选择;④交叉过程：采用单点交叉法对选择的染色体进行交叉操作;⑤变异过程：选择其中染色体对其基因进行变异;⑥终止条件：当程序满足终止条件时结束。本文模拟中使用的参数条件与文献[6，11]中表面参数基本一致，具体内容如表1所示。

2 ?结果与讨论

2.1 算法流程及模拟参数设置

对超疏水表面优化进行求解得到相应的结果如表1所示。与图3的换热能力进行对比可以发现，对于尺寸参数re/l和d/l来说，存在一定的最优化的结果。根据图中的换热变化趋势可知，re/l=1和d/l=0.35存在最强的换热能力。表2展示了不同遗传算法迭代次数下的优化结果。随着迭代次数的增加，遗传算法结果会逐渐逼近最优结果。但是可以发现，对于不同迭代次数下的表面最优换热能力差别并不显著。说明在节约计算资源的前提下可以选择较少的迭代次数，也能得到满足一定条件的最优化结果。

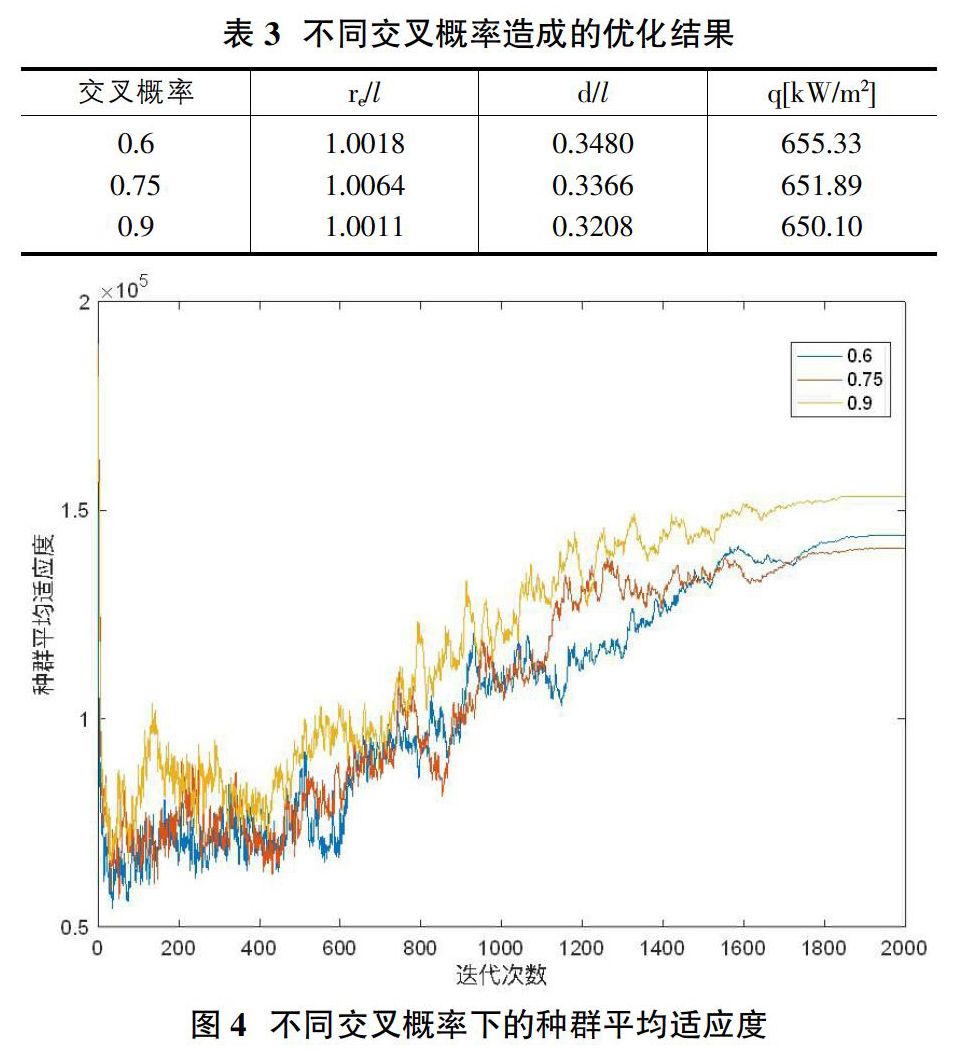
2.2 遗传算法交叉概率对结果的影响

在迭代次数为2000，交叉概率为0.7的前提下，不同交叉概率对超疏水表面结构优化求解的相应结果如表3所示。可发现，在0.6～0.9的范围内，交叉概率越小，得到的最优导热系数越大，优化结果越好。结合图4可发现，交叉概率为0.6时其平均适应度在迭代过程中总体来说低于另外两种情况，且在迭代1600次后平均适应度就趋于稳定。

因此在遗传算法迭代过程中，设置的交叉概率不宜过大，0.6左右为宜，且基于遗传算法运算效率和计算成本考虑，迭代次数无需过大即可得出比较好的结果，设置为1600～1800次为优。

2.3 遗传算法变异概率对结果的影响

在迭代次数为2000，交叉概率为0.6的前提下，不同交叉概率对超疏水表面结构优化求解的相应结果如表4所示。由表格可以看出，当变异概率为0.8时，所得到的导热系数更高，表面结构参数参数更优。且由图5可见，种群平均适应度在迭代次数达到1800次左右就趋于稳定，相较较大的迭代次数1800已有较好的优化结果，适当降低迭代次数可节约计算量以及计算时间。

因此在优化过程中，变异概率适宜定为0.8，结合2.2交叉概率的分析，迭代概率适宜设置为1800次左右。

3 ?结论

基于遗传算法对具有弹跳凝结的超疏水表面结构特征进行优化，对超疏水表面换热模型构建相应的遗传算法模型，并针对相关的遗传算法相关参数对优化结果的进行相应的讨论。超疏水表面结构参数优化结果对工程设计提供一定的工程设计依据。结果表明：

①超疏水表面结构参数合并尺寸和纳米柱直径对换热具有明显效果，合并尺寸越小和纳米柱直径越大，冷凝超疏水表面换热效果越好;

②迭代次数越大，优化效果越好，但达到一定迭代次数后优化效果的变化微小，考虑到程序运营的高效性，可将迭代次数设置为优化效果趋于稳定左右的数值;

③交叉概率对优化结果具有重要的影响，交叉概率越小优化结果越好，说明交叉概率对种群演化的稳定产生一定阻碍;

④变异概率会影响收敛结果的稳定性，变异概率在0.7～0.9之间处于0.8时具有较高的换热量，此时过大和过小的变异概率都会使得较差。

参考文献：

[1]ROSE J W， GLICKSMA.LR. Dropwise condensation - distribution of drop sizes [J]. International Journal of Heat and Mass Transfer， 1973， 16（2）： 411-25.

[2]BOREYKO J B， CHEN C H. Self-propelled dropwise condensate on superhydrophobic surfaces [J]. Phys Rev Lett， 2009， 103（18）： 184501.

[3]MILJKOVIC N， ENRIGHT R， WANG E N. Effect of Droplet Morphology on Growth Dynamics and Heat Transfer during Condensation on Superhydrophobic Nanostructured Surfaces [J]. Acs Nano， 2012， 6（2）： 1776-85.

[4]YAN X， ZHANG L， SETT S， et al. Droplet Jumping： Effects of Droplet Size， Surface Structure， Pinning， and Liquid Properties [J]. ACS Nano， 2019， 13（2）： 1309-23.

[5]KIM S， KIM K J. Dropwise Condensation Modeling Suitable for Superhydrophobic Surfaces [J]. J Heat Trans-T Asme， 2011， 133（8）.

[6]MILJKOVIC N， ENRIGHT R， WANG E N. Modeling and Optimization of Superhydrophobic Condensation [J]. J Heat Trans-T Asme， 2013， 135（11）.

[7]ZHANG L， XU Z， LU Z， et al. Size distribution theory for jumping-droplet condensation [J]. Applied Physics Letters， 2019， 114（16）.

[8]SHANG Y， HOU Y， YU M， et al. Modeling and optimization of condensation heat transfer at biphilic interface [J]. International Journal of Heat and Mass Transfer， 2018， 122（117-27）.

[9]CHEN X， WU J， MA R， et al. Nanograssed Micropyramidal Architectures for Continuous Dropwise Condensation [J]. Advanced Functional Materials， 2011， 21（24）： 4617-23.

[10]王燕青，唐萬生，韩其恒.基于遗传算法的概率准则组合证券模拟求解[J].管理科学学报，2002，5（6）：29-33.

[11]MILJKOVIC N， ENRIGHT R， NAM Y， et al. Jumping-droplet-enhanced condensation on scalable superhydrophobic nanostructured surfaces [J]. Nano Lett， 2013， 13（1）： 179-87.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。