《迷宫问题中最短路径问题的探究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

迷宫问题中最短路径问题的探究

范文

韩霖

摘要：经典的最短路径算法——Dijkstra算法是目前多数系统解决最短路径问题所采用的理论基础，该文通过对Dijkstra算法的研究，给出利用Dijkstra算法求解“迷宫”的最短路径的方法，进一步探究经过固定点的最短路径，并建立简单的整数规划模型通过Lingo软件进行求解此种情况下的最短路径。

关键词：最短路径；迷宫问题；Dijkstra算法；整数规划；Lingo

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2018）33-0055-02

1 问题描述

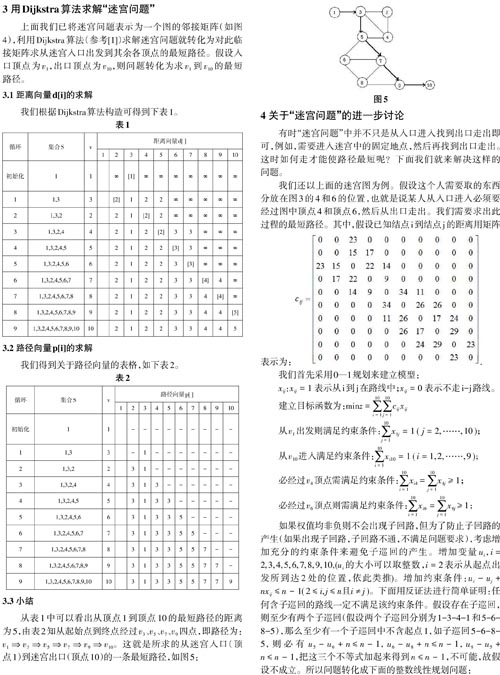
迷宫问题早在古希腊时就已出现，如今迷宫又以游戏程序的形式呈现在我们日常使用的电脑和手机上，求解迷宫问题的基本思想是如何寻找从入口到出口的一条路径，其基本算法主要包括传统算法及智能算法两大类。利用Dijkstra算法求解迷宫问题的关键在两点：一是如何把“迷宫”转换化为一个带权图；二是如何使用Dijkstra算法求从入口到出口的最短路径。战略决策、机器人路径规划等许多智能问题都可转化为寻找迷宫最短路径问题。从迷宫的入口到出口的路径有多条，最短的路径是哪条一直都是人们探讨的重点。

2 迷宫问题转换为带权图的邻接矩阵

迷宫中的位置采用二维数组存储，任何位置记作a[i][j]，当a[i][j]=0，则有通路，如果a[i][j]=1，则无通路。按照这样的规定我们求入口到出口的一条最短路径。

接下来用邻接矩阵进行存储，需要找到迷宫问题中所有值为0的点的个数为节点个数，令i为这些点中第i个节点，此点其八个方向为0的点作为i的邻接点。由于邻接表的顶点存储方式为散列存储，我们把每个为0的元素定义一个序号，不妨在二维数组中按行优先的规则找到为0的元素并按照顺序设置序号，这样邻接点节点既有行号列号，又有此节点作为顶点节点的位置，采用二维数组来存储，当a[i][j]为0时，b[i][j]存储a[i][j]的序号，否则为0。以图1所示的迷宫问题为例，由上面分析得到数组b的存储（如图2），（其中b[i][j]为0无通路，b[i][j]非0则有通路）。

因为须求出从入口到出口的最短路径，则要给出表示迷宫的带权图的邻接矩阵。最短路径即是从入口到出口经过边数最少的路，所以，约定每相邻接的两个顶点间的权值为1，令邻接矩阵中第i行第j列的元素为[aij]，则邻接矩阵可定义为：

3 用Dijkstra算法求解“迷宫问题”

上面我们已将迷宫问题表示为一个图的邻接矩阵（如图4），利用Dijkstra算法（参考[1]）求解迷宫问题就转化为对此临接矩阵求从迷宫入口出发到其余各顶点的最短路径。假设入口顶点为[v1]，出口顶点为[v10]，则问题转化为求[v1]到[v10]的最短路径。

3.1 距离向量d[i]的求解

我们根据Dijkstra算法构造可得到下表1。

3.2 路径向量p[i]的求解

我们得到关于路径向量的表格，如下表2。

3.3 小结

从表1中可以看出从顶点1到顶点10的最短路径的距离为5，由表2知从起始点到终点经过[v3]、[v5]、[v7]、[v9]四点，即路径为：[v1?v3?v5?v7?v9?v10]。这就是所求的从迷宫入口（顶点1）到迷宫出口（顶点10）的一条最短路径，如图5：

4 关于“迷宫问题”的进一步讨论

有时“迷宫问题”中并不只是从入口进入找到出口走出即可，例如，需要进入迷宫中的固定地点，然后再找到出口走出。这时如何走才能使路径最短呢？下面我们就来解决这样的问题。

5 结束语

本文給出了解决“迷宫问题”最短路径的方法，把迷宫问题转化成一个带权图，利用Dijkstra算法求出从入口到出口的一条最短路径，并且对“迷宫问题”做进一步讨论，对于有限制条件的“迷宫问题”，通过简单的整数规划方法并利用lingo软件求解经过固定点的最短路径。

参考文献：

[1] 胡运权.运筹学基础及应用[M].北京：高等教育出版社，2008.

[2] 卜月华.图论及其应用[M].南京：东南大学出版社，2000.

[3] 严蔚敏，沈佩娟.数据结构[M].北京：国防工业出版社，1982.

[4] 杨淑群.迷宫问题转变成图的问题的讨论[J].计算机与现代化，2003（2）：10-11.

[5] 朱素英.迷宫问题的图论解法探讨[J].湖南人文科技学院学报，2006，6（3）：73-74.

[6] 马良.旅行推销员问题的算法综述[J].数学的实践与认识，2000，30（2）：156-157.

[7] 陈芳芳，姜忠义，吴春青.运筹学教学中的动态规划求解最短路径问题的一个注记[J].高师理科学刊，2016（9）.

[8] 徐天亮.运输与配送[M].2版.北京：中国物资出版社，2012.

【通联编辑：代影】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。