《基于BP神经网络的电梯制动距离预测系统》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于BP神经网络的电梯制动距离预测系统

范文

盖晓东李溪水秦文江黄启斌卢俊文

摘要：针对现有电梯制动距离预测系统容易受到外界噪声干扰、忽略制动传感器数据的问题，设计一种基于BP神经网络的制动距离预测系统。该系统从电梯控制系统和电梯预测模型两方面對电梯运行状态进行监测和预测，可根据电梯制动系统和末端行程系统的运行参数，对电梯制动距离进行准确预测。为验证系统有效性，利用单片机搭建了实验仿真平台，在不同应用环境下对电梯的制动距离预测进行了大量实验。实验结果表明，该系统操作简单、可扩展性好，能有效解决复杂环境下电梯制动距离的准确预测。

关键词：电梯控制;BP神经网络;正则化;制动距离

中图分类号：TP311? ? ?文献标识码：A

文章编号：1009-3044（2019）23-0200-03

开放科学（资源服务）标识码（OSID）：

1 引言

完善的电梯故障检测和预警技术是电梯安全运行的重要保证。当电梯发生故障时，电梯紧急制动能力固然重要，若能准确预测电梯运行状态的实时变化，不但能为系统决策提供有力依据，还能发挖掘电梯潜在运行故障，进而做到防患未然。

电梯的运转过程，在理论上可抽象为制动器的“旋转-直线”运动模型。为此，文献[1]以数学模型设计了电梯制动力矩。在文献[2]中详细分析电梯制动器的力学结构，并以此建立理论模型，给出典型客梯运行过程中制动距离与制动时间的关系。

然而，在电梯的实际运作过程中，由于钢索与曳引轮间摩擦、曳引轮自身阻力、轿厢与导轨间摩擦、负载变化等多种因素影响，使得运行状态的预测异常复杂。为解决以上问题，文献[3]应用RBF神经网络预测电梯的制动距离，该方法可有效逼近电梯制动距离的非线性变化关系。文献[4]设计一种基于马氏距离和粒子群算法的神经网络算法，可快速预测电梯故障信息。文献[5]将BP神经网络应用于电梯控制系统，在运行时间和动态分区原则的约束下，计算出最优调度策略。然而，以上方法仅考虑电梯轿厢的运行参数信息作为神经网络输入，而忽略了制动器相关数据（如制动力），很难达到精确预测。

本文将从电梯控制系统（包括制动器和轿厢）和智能预测模型两方面入手，就电梯制动距离进行实时检测和预测。图1给出了本文系统工作原理图。本系统可分为训练和测试两个阶段。在训练阶段，系统扫描安装于电梯轿厢和制动器上的传感器，在时间序列上捕捉电梯的运行状态数据，如制动器压力、制动器转速、轿厢重量及轿厢速度等参数;其后对采集到的数据进行预处理，如删除无效数据、归一化处理等;最后将数据输入到BP神经网络中训练模型。在测试阶段，系统采取与训练阶段同样的方式收集传感器数据，将数据输入训练阶段所获得模型，最终得到预测结果。

2 BP神经网络

2.1 网络结构

BP（Back Propagation）神经网络是20世纪80年代被提出的一种结合误差反向传播算法的多层前馈网络。由于其网络结构简单，且能够有效处理输入-输出数据的复杂非线性关系，得到了广泛的应用。BP神经网络结构可分为输入层、隐藏层和输出层，每一层均有若干神经元（以下简称节点）。其中，输入层和输出层的神经元数由训练样本属性决定，而隐藏层的节点数则需根据模型复杂度设定。以往研究表明，若提供足够多隐藏层节点数，则一个3层的BP神经网络结构可实现任意[n]维到[m]维数据的映射[6]。

图2展示了一个典型的3层神经网络结构，可以看出每一层的节点与上一层的节点之间相连。例如，在隐藏层，每个节点是输入层节点的线性组合，而该层节点的输出是经过激活函数调整后的值。对神经网络的训练过程，即为确定层与层之间链接的权重值。为衡量网络模型训练的合理性，需要有效模型预测值与目标值逼近程度。以均方误差（Mean Squared Error， MSE）为例，设共有[n]组待测试数据，第[i]组数据的预测值和真实值分别为[yi]和[yi]，则MSE可表示为：

[1ni=1nyi-yi2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?][1]

MSE值越小，代表预测的结果越准确。

2.2 正则化网络结构

当数据样本较少时，网络模型的训练过程很容易出现过拟合现象。为提高BP神经网络的泛化能力，一种有效的方法是为模型增加正则化项。引入正则化项后，BP神经网络的目标函数可表示为：

[γMSE+（1-γ）MSW? ? ? ? ? ? ? ? ? ? ? ? ? ? ?2]

其中，[γ]是调节因子，设[w]为模型的权重向量，MSW定义为：

[MSW=1ni=1nw2i? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?3]

3 实验环境搭建与数据采集

3.1 数据采集

本小节详细描述系统实验仿真环境搭建及传感器数据采集的实现细节，所实现实验仿真平台如图3所示。

可看出，系统主要由轮盘、压力传感器、光栅、光栅读头、制动片、钢线绳、控制器、载重托盘等组成。其中，压力传感器采用大洋DYMH-02膜盒式荷重传感器（0-5kg），光栅采用150LPI压电写真机光栅带，光栅读头为H9720工正解码器、控制器采用Arduino UNO R3、轮盘测速传感器采用ASLONG GA25-370G光电编码器。

仿真平台工作流程为：1）将砝码放置于载重托盘上;2）转动轮盘将载重托盘移动至初始位置;3）将制动片压在轮盘上，保证托盘处于静止状态;4）放松制动片，让载重托盘在重力作用下自由下落。同时，按下数据記录开关按钮，数据采集周期设置为10毫秒;5）当托盘到达指定位置时，松开数据记录开关按钮，保存数据，并结束本次数据采集。

3.2 数据预处理

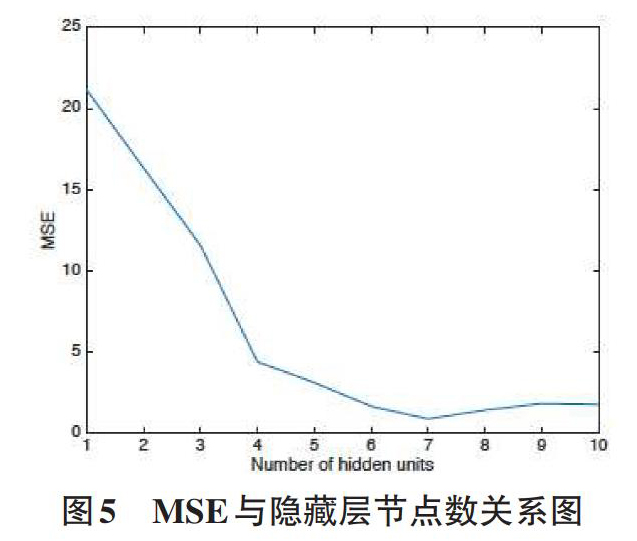
由于实验操作过程中，存在一定的人为操作导致的误差，需要对实验数据进行筛选。考虑到预测系统的实际应用场景很难支持实时的人为数据处理。通过对所采集到数据的观察，本文采用相邻数据间变化规律剔除冗余数据，主要包括电梯静止状态和停止状态下的冗余数据。设[t]时刻所采集到数据向量为[xt=[x1t，x2t，…，xdt]]，其中[d]代表电梯运行参数的种类数，如电梯的速度、制动距离和制动力等。设[t+1]时刻采集到的数据向量为[xt+1=[vt+1，dt+1，…，pt+1]]，若[absvt+1-vtvt

为消除数据特征差异性对神经网络可能造成的影响，需要将数据特征进行归一化处理。本文将数据的所有特征均归一化到[-1，1]区间内。设数据某一特征中数值最大值和最小值分别为[fmax]和[fmin]，待归一化的数据为[x]，则归一化后的数据[y]可表示为：

[y=2*（x-fmin）fmax-fmin-1，? ? ?if fmax≠fmin0.5，? ? ? ? ? ? ? ? ? ? ? ? ? if fmax=fmin? ? ? ? ? ?（4）]

4 实验结果与分析

为验证本文所提出方法的有效性，就电梯制动距离预测准确度与轿厢速度、制动力、运行时间的相关性进行详细分析。

4.1 实验设置及评价指标

本文采用BP神经网络采用3层网络结果，包括输入层、隐藏层和输出层。其中，输入数据特征为载重（单位g）、轿厢速度（m/s）、制动力（N）和运行时间（ms），即输入层节点数为4; 隐藏层的节点数为7;输出结果为待预测的距离（m），即输出层节点数为1。神经网络的迭代数数（epochs）设置为100，目标误差（goal）设置为[10-4]，正则化因子（regularization）设置为[10-10]。在模型训练过程中，将数据样本分别按照0.7， 0.15和0.15的比例划分为训练数据集（training set）、验证集（validation set）和测试集（testing set）。

本系统旨在使预测结果与真实结果尽量逼近，同时，为有效评价单组数据预测的准确度并删除数据大小差异所带来的影响。设真实值为[x]，预测值为[y]，定义单组数据预测误差为：

[x-yx? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?5]

4.2 电梯制动距离预测结果

表1-表3分别展示了本文方法在系统负载为500g、600g和700g时的预测结果。从表1中可以看出，预测的误差值随着轿厢速度的逐渐增大将不断减小，且该现象在表2和表3中也表现得较为突出。例如，在表2中，当轿厢速度为0.1396时，预测的误差达到22.24%。随着负载重量的增大，预测误差也出现逐步减小的趋势。例如，当负载为700g，且轿厢速度为0.1396时，预测误差为3.05%。出现这些现象的主要原因，可能是当轿厢的速度和载重较大时，外界噪声的干扰将会得到抑制，进而有效提高预测的准确度。图4展示了本文预测结果与真实结果的对比图，从图中可以看出当轿厢速度越快（曲线越陡）时，预测方法能更准确地对数据建模。

4.3 预测准确度与隐藏层节点数关系

BP神经网络训练过程中一项重要的工作是需要确定隐藏层节点数（以下简称节点数）。通常节点数越多，模型的表达能力越强，模型也越复杂。但节点数也并非越多越好，若节点数过多则必然导致模型的参数增大，在训练样本有限的情况下，很容易出现过拟合现象。

为确定最佳节点数，本文研究了模型在不同节点数情况下的MSE。在本次实验中，采用与3.1小节相同的参数设置方法。由于模型对于参数的初始值较为敏感，对于每个节点数重复实验5次，然后取5次实验结果的平均值作为该节点数下模型的最终结果。图5展示了本次实验结果。从图中可以看出，当节点数较少时，如1个节点，模型拟合的效果较差，MSE将近21，其可能的原因是节点数过少时模型出现欠拟合;随着节点数的不断增加，MSE也随之减少;当节点数为7时，模型拟合效果达到最佳;当节点数超过7时，MSE呈现略微增加趋势，其可能的原因是节点数过多时模型出现过拟合。因此，节点数7是本文模型的最佳选择，这也是本文第3.1小节中，将隐藏层节点数设置为7的原因。

5总结

为解决复杂环境下电梯制动距离的准确预测，本文提出一种基于BP神经网络的预测系统。该系统融合了电梯制动器和电梯末端系统的运行参数，并借助BP神经网络实现制动距离的预测。为验证系统有效性，在单片机上配合多种类型传感器，构建了一套电梯制动距离监测和预测系统。实验结果证明了本文所提出设计方案的可行性。在未来工作中，将重点研究电梯制动距离的在线预测方法。

参考文献：

[1] 叶穆. 上上下下的安全卫士——电梯制动系统专题：电梯制动器的制动减速度和制停距离分析[J]. 中国电梯， 2007：15-17.

[2] 陈传斌. 电梯制动器的结构和制动力的理论分析与计算[J]. 中国特种设备安全， 2007，（12）：47-50.

[3] 丁宝，唐海燕，丁艳虹，等. 电梯零速停靠的RBF神经网络预测算法[J]. 哈尔滨工业大学学报， 2009（7）：64-67.

[4] 王赛男，陈敢. 基于改进神经网络的电梯故障诊断[J]. 长江工程职业技术学院学报， 2018（2）：25-27.

[5] 刘剑，梁延东. 电梯运行的神经网络控制[J]. 沈阳建筑工程学院学报， 1999， 15（3）：289-292.

[6]焦斌，叶明星. BP神经网络隐层单元数确定方法[J]. 上海电机学院学报， 2013（3）：113-116.

【通联编辑：梁书】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。