《细菌觅食优化算法研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

细菌觅食优化算法研究

范文

吴进周昊

摘要：在管理、经济、工程和科技领域中，常需要求解多约束条件下的最优解问题，群体智能算法是常用的求解方法。细菌觅食优化算法（BFO）是近年来提出的一种新型的群体智能算法，不仅在群体智能优化理论中具有学术意义，在动态、多目标、多约束等复杂条件下的工程优化求解问题中也具有巨大的应用价值。

关键词：细菌觅食优化算法;群体智能算法;智能优化算法;BFO

中图分类号：TP18 文献标识码：A

文章编号：1009-3044（2020）06-0073-02

1背景

在实际的工程等领域中，人们常需要选择最合理、最优的解决方案，即“求解最优解”问题。从数学家求解多元函数极值问题开始，到解决非线性规划问题等，最优化理论的研究逐步得到进展，各种优化方法成为研究热点。20世纪90年代左右，学者们从大自然中找到灵感，研究了生物启发式算法——群体智能算法，如PSO等。近年来，学者从大肠杆菌在人体肠道内的觅食行为，提出了细菌觅食优化算法fBacterialForagingOpti-mization，BFO），成为群体智能算法的又一研究热点。

2细菌觅食算法基本原理

细菌作为最简单的、最古老的无核单细胞生物，具有强韧的生命力，和对复杂环境的适应性，显示了其生存活动过程中的优化本能。大肠杆菌的觅食行为主要过程可以分为3个步骤：1）寻找可能存在的食物区域;2）判断是否进入该区域;3）经过一段时间的食物消耗后，或者当前环境变得恶劣不适宜生存，细菌消亡或者迁移到其他适宜的觅食区域。

BFO算法具有并行搜索、易跳出局部极小值等优点，被广泛运用于图像处理、自动控制、神经网络训练等多方面问题。细菌觅食优化算法主要以趋化、复制、消亡与迁移等三种算子进行迭代和搜索最优解，以及种群进化。其中最关键的是趋化算子，模拟的是细菌的趋化过程，翻转（Iumble）和游动（swim）。

3细菌觅食优化算法的优化流程

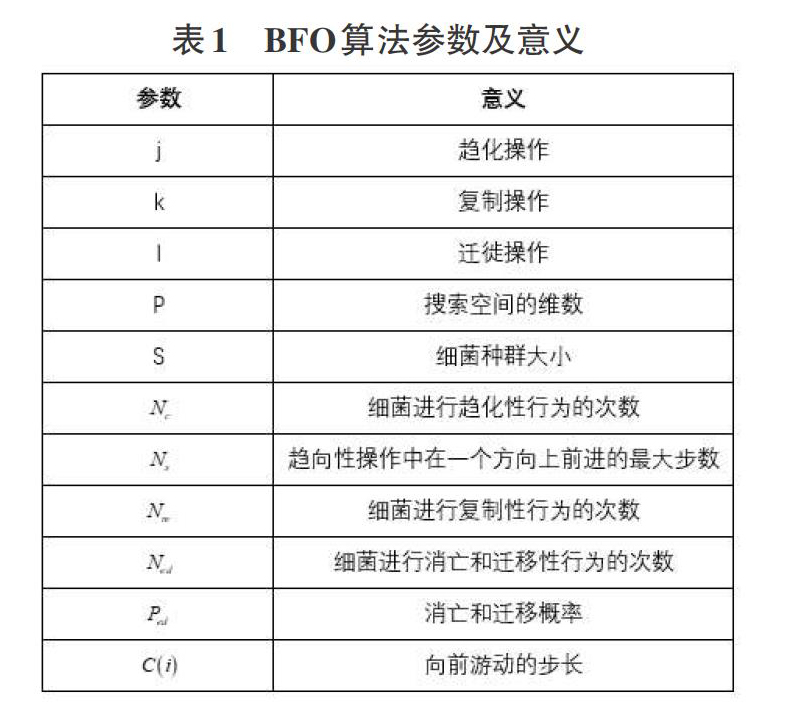
步骤1：初始化种群，包括各种参数。如表1所示。

步骤2：设计评价函数，并求出当前群体各个体的最优解。

步骤3：种群进化。分为三层循环：

（1）迁移循环（1-1+1）

（2）复制循环（k=k+1）

（3）趋化循环（j=i+1）

步骤四：算法结束，输出群体最优解。

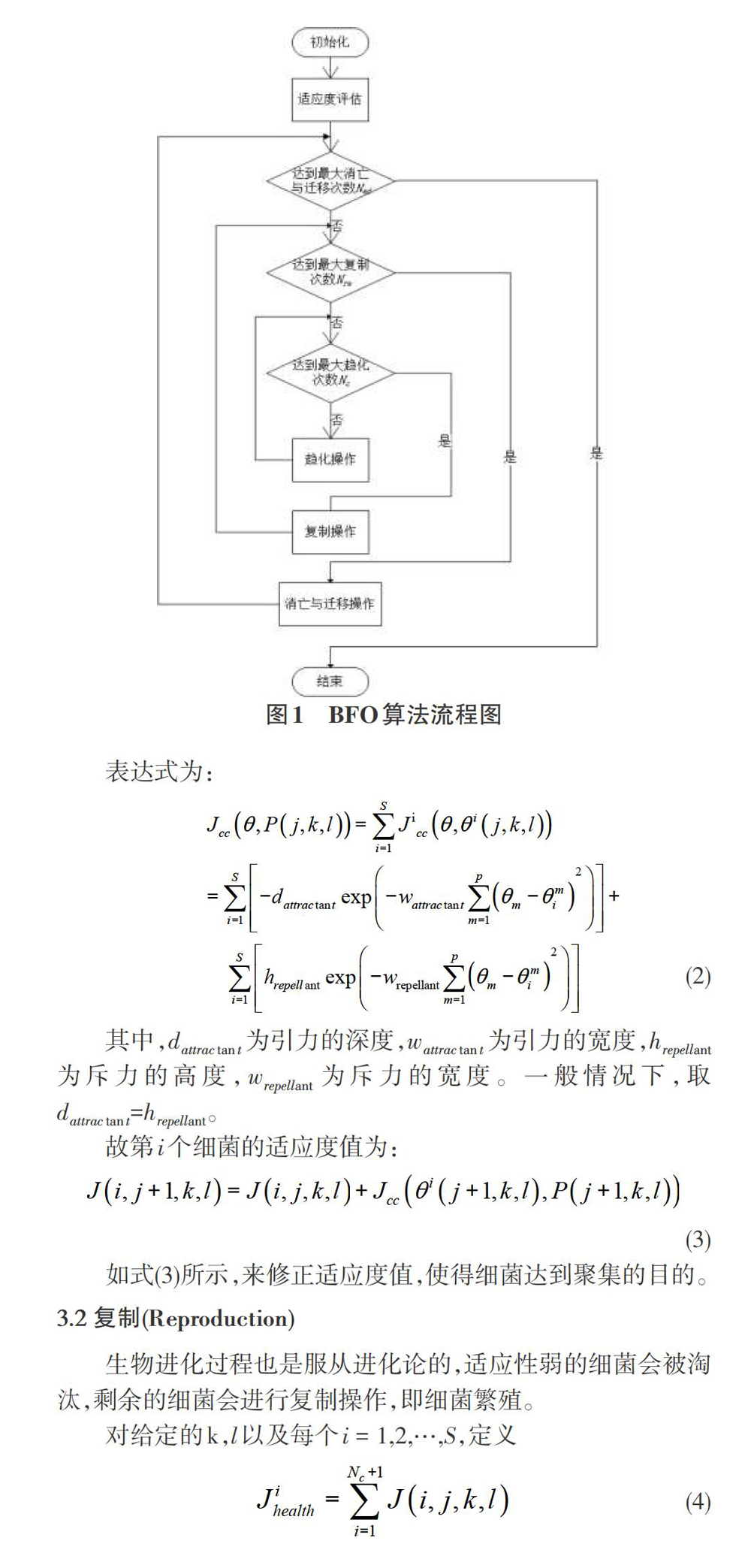
整个算法流程图如图1所示。

3.2群体交流（即聚集性操作Swarming）

细菌觅食过程中会有交流聚集行为。细菌之间既有引力又有斥力以释放信号。斥力使其他细菌保持安全距离，不要向其游动。引力使细菌聚集在一起，吸引其他細菌向之游动。

3.3消亡及迁移（Elimination and Dispersal）

当细菌环境改变时，如食物逐渐耗尽或者其他变化f如温度突变等），该区域的细菌种群就会迁移到新的适宜的地方，或者就是死亡。在BFO算法中称为消亡及迁移操作。

迁移操作让细菌以概率Ped被随机重新分配到另外的空间区域，原来的细菌个体死亡，并在解空间的其他随机位置产生新个体。这些新个体也许比较接近全局最优解，从而有利于趋向操作跳出局部最优解，进而可以在全局寻找最优解。

4细菌觅食优化算法的应用分析

与其他群体智能算法相比，细菌觅食优化算法比较简单、灵活，也可以与其他各种算法结合产生新的优化算法，可以解决多方面的应用问题，具有比较强的适应性和鲁棒性。可以用于图像处理方面，如图像分割、图像增强、特征抽取、人脸识别、图像配准等;可用于电力系统优化方面，如最优潮流设计、发电控制参数优化、电力系统经济调度、谐波评估等;可用于智能控制方面，如电磁装置优化控制、太阳能追踪控制系统、非线性动态系统等;可用于参数优化选择方面，如各种控制器的参数设计等;可用于经济管理方面，如车间作业调度问题、股票预测等;还有生物信息学DNA序列主题发现等。但是细菌觅食算法也有不足，如算法参数比较多比较复杂，计算复杂性较大。

5总结

BFO算法作为群体智能算法中的新的医院，已引起了国内外大量学者的关注和研究，但是大多数是针对具体的应用场景，很少是针对算法本身的研究，未来的研究应该从算法参数改进、算法简化等学术研究上加以创新，以提高理论深度与应用价值。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。