网站首页  词典首页

标题	浅谈协作机制在高中数学教学中的合理应用
范文	杜云丰 [摘 要] 数学知识的学习探究，无处不需要协作. 协作的主体并不仅仅限于学生范围内，教师同样也应当成为参与协作的重要角色. 通过协作，学生之间相互讨论，相互寻找问题，共同探究方法. 教师也可以借助这一途径适时地对学生的思维加以引导和启发，将教学行动隐于无形. [关键词] 协作机制；高中数学；合理应用 数学学习并不是单打独斗的过程，而是需要来自各方的不断协作来予以推动和实现的. 数学本就是一门灵活变化的学科，我们无法用固化的模式和范围对之加以限定，只能通过找寻数学知识当中的脉络和规律来对其加以掌握. 因此，如果在这个过程当中始终只依靠某一个人的力量，是很难快速完整地捕捉到数学的全貌的. 高中阶段的数学知识，从灵活性和深入性上都表现得十分明显，这便更需要借助协同合作的力量，为知识掌握点燃更多思维的火花. 这也就是我们即将在文中讨论的协作机制在高中数学教学中的合理适用的问题. 对课前预习协同合作，点燃探究热情 无论何种知识，想要在学习过程中收获理想的效果，就一定不能忽略了课前预习的步骤. 预习对于整个学习活动的开展来讲，是非常关键的前期基础. 从知识本身来讲，通过预习，学生能够提前接触知识，自行明确学习重点和难点所在，让课堂学习更具针对性. 从心理状态来讲，让学生提前感知知识，能让他们做好心理准备，面对主体学习时不至于手足无措. 既然课前预习如此重要，自然要选择合理的方式予以实现，协同合作便是其中的一种. 例如，学生在对集合概念的内容进行预习时，笔者为大家设计了这样一个问题：已知集合A，B，C，D，且A?B，A?C，若B={0，1，2，3，4}，C={0，2，4，8}，则集合A最多含有多少个元素？集合A最多含有多少个子集？并请大家在思考这个问题的同时找出这部分知识学习的重点所在. 果然，每个学生对此都有自己的看法. 有的学生认为，弄懂“元素”与“子集”的基本概念是最重要的，这样才能准确地把握题目要求. 有的学生则认为，学习中最关键的是要弄明白集合元素与子集的性质，这样才能判断出结论正确与否. 还有学生表示，集合之间的关系也是一个学习重点，这样才能将已知条件把握清楚. 在大家的协作之下，预习环节中所初步总结出的知识要点已经比较全面了. 课前预习的工作如果只交给学生个人去做，往往会让大家在初次接触知识内容时不容易建立起深刻的印象. 在独自阅读和思考时，学生难免会出现理解与认知上的问题，而面对这些问题的却只有学生自己，这其中的很多问题便会不了了之，被学生所忽略，无法在接下来的学习中起到方向性作用. 另外，独自预习的形式也很难激发起学生的自主热情，对于高质量完成课前预习也是不利的. 对新知接受协同合作，全面发掘感知 新知识的呈现是高中数学教学的核心环节，自然也是协作教学模式所应适用的重点领域. 很多教师为了保证教学效率，总是将呈现知识内容的主动权全部掌握在自己手里，时刻对学生提要求，而学生则始终处于被动接受的位置上. 从新时期的教学理念角度来看，这种角色设置是不够合理的. 归根结底，学生才是知识内容的最终接受者，因此，教师有必要让他们对知识的产生过程进行充分的感知和参与，这样才能真正地将教学活动落实到位. 例如，在立体几何知识的学习中，空间中直线的位置关系是一个十分重要的基础性知识. 为了让每个学生都能够加入到具体分析的行列当中来，笔者将全班学生分为四组，并给每组分配了一个命题，请组内成员协作运用所学知识来判断命题的正误，这四个命题分别为：①l1⊥l2，l2⊥l3?l1∥l2；②l1⊥l2，l1∥l3?l2⊥l3；③l1∥l2∥l3?l1，l2，l3共面；④l1，l2，l3共点?l1，l2，l3共面. 每个小组针对自己所分配到的问题，都展开了热烈的讨论. 有的学生从理论角度进行推导，有的学生则从反面寻找特例. 大家不仅最终得出了正确的判断，更成功将这部分知识内化于心了. 通过学生之间的协同合作，整个高中数学课堂都展现出了全新的面貌. 学生不再是等着教师来提供知识，而是主动投入到知识发掘的过程当中来，积极地去发现和推理，并在同其他学生的讨论交流当中，不断地充实现有的知识体系. 这样的做法，能够让教学效率显著提升起来，并使得学生对于新知识的印象尤其深刻. 初始的思维印象对于接下来很长一段时间的学习深化都是具有重要影响作用的. 对典型问题协同合作，发现思维规律 高中数学中出现疑难复杂问题的频率还是比较高的，这也是很多学生感到学习困难的重要原因所在. 为了能够让学生妥善地应对、处理这些问题，教师有必要在日常教学过程中将这类问题着重提出来，并带领大家有针对性地对之予以关注和重点分析. 将典型问题纳入到常规性教学训练之中后，学生在各类考试当中再遇到新形态的疑难复杂问题时，也就不会再感到手足无措了. 谈及这类问题的教学方式，鉴于其中思维的多元性和复杂性，协同合作的学习方式也就必不可少了. 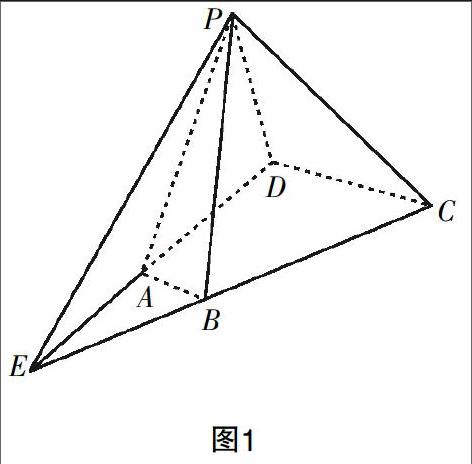例如，学生曾被这样一个立体几何问题难住了：在梯形ABCD中， ∠ADC=90°，AB∥CD，AB=1，CD=2，AD=，P为平面ABCD外一点，PAD是正三角形，且PA⊥AB. 求平面PBC与平面PAD所成二面角及点D到平面PBC的距离. 通过补充图形（如图1），问题得解. 由此，笔者不断启发大家发现其中的思维规律，在讨论与探究中，找到了无棱二面角问题的三个解答途径：一是由二面角两个面内的两条相交直线确定棱，二是由二面角两个平面内的两条平行直线找出棱，三是补形构造几何体发现棱. 教师在对这类问题进行教学设计时，首先要树立这样一种意识：我们要做的并不仅仅是让学生将这一道题解答出来，而是要以此为代表，让学生從中发现解题规律，有效整理思维，进而将这种有效思考的方法自主运用到其他相类似的问题解答当中去. 然而，思维规律是十分抽象的东西，仅靠语言描述是不够的，而需要学生用心去感知. 在协作学习的氛围之下，学生得以近距离触摸到分析解答问题的过程，探究效果自然是比较理想的. 对课后评价协同合作，探寻薄弱所在 对于一次完整的课堂教学来讲，结尾处的评价环节至关重要. 特别是对于高中数学教学来讲，知识难度与密度的提升让不少学生无法在课堂之上将知识内容完全掌握，那么，这种薄弱之处定然是会从一些细节表现出来的. 如果能够将这些地方及时发现，并在评价环节予以明确，将会成为推动教学完善的强大动力. 教学实践表明，以协同合作的方式开展课后评价，往往能够更好地实现预期效果. 例如，在解析几何部分椭圆内容的教学过程中，笔者发现很多学生容易在离心率的问题上出现问题. 于是，在课后评价环节，笔者请大家解答如下问题：若椭圆的两准线之间的距离不大于长轴长的3倍，则它的离心率e的范围是多少？果然，有的学生的答案是. 还没有等笔者开始分析，学生已经开始很主动地相互讨论找原因了. 最终发现，不少学生之所以出错，是因为自己只注重了对显性已知条件的翻译，却忽略了“椭圆离心率0在以往的数学教学当中，课后评价常常是由教师一方做出的. 但是，仅凭教师一人，无法将学生的学习欠缺之处总结完全，也无法让学生亲身融入其中去感受到薄弱环节之所在. 那么，课后评价的内容便没有真正走进学生心里，大家的理解效果更是难以达到理想了. 协作评价的进行，让每个学生都参与到寻找问题和解决问题当中来，从评价效率和评价效果上都是我们希望看到的. 可以看到，高中数学教学的各个阶段都能够成为协作机制适用的土壤. 的确，数学知识的学习探究，无处不需要协作. 协作的主体并不仅仅限于学生范围内，教师同样也应当成为参与协作的重要角色. 通过协作，学生之间相互讨论，相互寻找问题，共同探究方法. 教师也可以借助这一途径适时对学生的思维加以引导和启发，将教学行动隐于无形. 经过一段时间的协作教学实践，学生的主动学习意识明显增强了，在面对疑难复杂问题时，思维方式也灵活了许多. 协作的模式，也为高中数学课堂带来了更多生机，学生普遍感到学习过程没有那么刻板枯燥了，对于数学学习自然增加了不少热情.
随便看	论证券投资中的风险识别与防范 签有盈利预测补偿协议的互联网企业并购风险研究 多元化股权投资与公司债券融资成本的关系探析 从金融供给侧改革角度看科创板意义 新形势下国有企业股权投资的常见问题及对策分析 对当代商业银行表外业务的思考 军工科技金融服务平台研究 我国私募股权投资基金IPO退出机制的法律研究 普惠金融对金融扶贫的作用探析 行政事业单位加强固定资产管理的思考 管理会计在中小企业的应用和探索 企业内部控制的现状及改进措施 事业单位、国有企业预算工作中的问题及对策探析 环境卫生管理事业单位做好内部控制策略探析 城市居民参与生活垃圾分类行为研究 论生活垃圾焚烧发电的污染源和环境保护策略 公立医院法人治理结构研究 施工企业工程投标管理探析 论信息技术对企业管理的影响 深化工程招投标监管的意义及措施 建设项目工程造价全过程管理的控制点分析 商业地产开发及经营管理存在的问题和对策 港口物流托盘监管的风险防控 高职院校物流专业现代学徒制人才培养模式探究 高校校园快递的现状及优化调整 bracketcreep bracketed bracketing bracketlike bracket's brackets bracket² bracket¹ brackish brackishness brackishnesses brad brag bragged bragger braggers braggery braggest braggier braggiest bragging braggingly braggy bragless bragly 癞蛤蟆上蒸笼——气鼓气胀 癞蛤蟆不吃人——相难看 癞蛤蟆不长毛——天生这路种 癞蛤蟆也有吃天鹅肉的日子 癞蛤蟆伸长脖子想吞月亮——想头倒不低 癞蛤蟆剖腹——心不死 癞蛤蟆剖腹心不死 癞蛤蟆剥皮不闭眼——还想蹦几下 癞蛤蟆剥皮不闭眼——还想蹦跶几下 癞蛤蟆剥皮眼不闭，黑甲鱼剖腹心不死 癞蛤蟆吃天——没法下嘴 癞蛤蟆吃天鹅肉——想得美 癞蛤蟆吃苍蝇——将供嘴 癞蛤蟆吃骰子——一肚子点子 癞蛤蟆吞蒺藜——吃了个哑巴亏 癞蛤蟆吹唢呐——有啥好听 癞蛤蟆喝浆糊——张不开嘴，干鼓肚 癞蛤蟆在阴沟里想着天鹅肉吃——如何到口 癞蛤蟆坐金銮殿——梦想 癞蛤蟆坐飞机——一坐登天 癞蛤蟆垫床脚 癞蛤蟆垫床脚——纵高也有限 癞蛤蟆垫板凳——死撑活挨 癞蛤蟆垫板凳——活挨死顶 癞蛤蟆垫桌腿——暗气暗憋

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。