《基于滑动自回归系统序贯回归算法的系统辨识》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于滑动自回归系统序贯回归算法的系统辨识

范文

吕小纳

摘要：系统辨识也即系统建模，本文主要研究在滑动自回归系统中使用序贯回归算法（SER）现实系统辨识。该文推导了滑动自回归系统中各级参数的序贯回归算法表达式，并验证了二阶系统的序贯回归算法的迭代过程。同时也验证了高阶滑动平均系统中算法的应用及准确性验证。通过验证可以得到序贯回归算法（SER）对滑动自回归系统能达到较高的辨识度。

关键词：序贯回归算法;滑动自回归系统;系统辨识

中图分类号：TP319? ? ? ? 文献标识码：A

文章编号：1009-3044（2020）16-0200-03

1 前言

系统辨识也即系统建模，根据系统的输入量与输出量，以及系统阶数预估的情况下，确定系统的各阶参数，本文主要是确定系统的转移函数。当系统转移函数被确定，则在输入和输出条件下的系统模型就被建立起来。根据建立起来的系统模型就可以由系统的输入函数确定系统的输出信号[1]。

本文主要研究滑动自回归系统的模型系统估计。使用的自适应算法为序贯回归算法（SER）[3]。序贯回归算法（SER）相比于LMS算法有这更快的收敛速度，但是其运算复杂度要高于LMS算法。随着微处理器性能的提升，复杂度较高的算法也能达到较高的实时性，同时又能达到较高的收敛速度。本文重点分析了滑动自回归系统中序贯回归算法（SER）的算法计算原理，并在二阶系数条件下验证了序贯回归算法（SER）的收敛过程。同时在高阶的滑动平均系统使用序贯回归算法也达到了较高的系统辨识。

2 基本理论

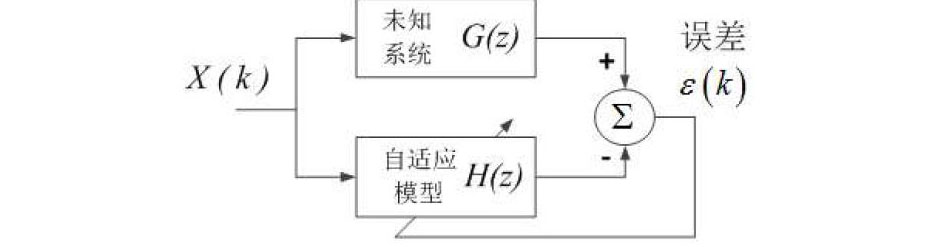
本文通过序贯回归算法（SER）构造自适应递归滤波器系统，系统结构如图1所示，通过SER算法可以使自适应模型收敛到未知系统。收敛的准确性受两个因素影响，一个因素是输入随机信号与期望输入信号之间的均方误差，另一个因素是未知系统的阶数，当自适应模拟选择的阶数与未知系统阶数一致时，收敛的结果可以达到较优的状态。

3 实验结果及分析

3.1 递归系统识别

递归系统即全极点系统，其系统识别的结构图如图2所示。当图2中的b0k=1，其他blk都等于0时，即为纯递归系统。系统辨识的目的是通过一步步迭代，使自适应模型系统的参数与未知系统参数一致。参数一致的判定标准为图1中的误差值为0。

若输入信号为確定信号，则未知系统的输出也是确定信号，同理系统的期望输出也是确定信号。理论上误差最小值可以达到0。但实际情况中输入信号往往是平稳随机信号，所有误差值只能收敛到一个较小的范围。误差最小值为[ξmin=Edk2-PTWopt]。[Wopt]为满足维纳-霍夫（Wiener-Hopf）方程的最优权向量。而[P=Ed*X]。根据维纳-霍夫（Wiener-Hopf）原理也可知误差值只能收敛到一个较小范围内。

当权值个数比较多时，所对应代价函数的维数就较多，为了方便地看到权向量收敛的过程，本文使用二阶系统来进行验证。为了简化收敛过程，本文只对b0，a1，a2进行自适应辨识。误差ε（k） = Y（k）-y（k），其中Y（k） =x（k）*g（k），g（k）为未知系统的冲激响应。

通过图3可以看出，只要系统为可实现稳定系统，不管初始权值在何位置，通过迭代最终都可以收敛到最佳权值附近。

3.2 非递归系统识别

对于纯非递归系统（即全零点系统），则图1中未知系统的系统函数为[Gz=B0+B1z-1+…+BLz-L]。由于非递归系统相比于递归系统，由于没有极点，所以在滤波器中要达到同样的滤波器效果所需的阶数较高。本文使用20阶非递归系统进行系统辨识。

4 总结

本文通过递归与非递归系统的基本结构，导出递归与非递归系统中均方误差对各个系数之间的梯度表达式。牛顿梯度搜索法中需要输入信号的自相关矩阵，由于实际情况中，输入信号是依次进入，难以获得输入信号的确定自相关矩阵。本文通过输入信号自相关矩阵的无偏估计代替自相关矩阵，推倒序贯回归算法（SER）的表达式。为了验证SER算法的准确性，本文使用二阶递归系统进行权值的迭代回归。通过实验可以看出权值最终会收敛到最佳权值附近。由于输入信号和输出期望信号的随机性，所以最终权值只能收敛到最佳权值附近。本文同时验证了SER算法在非递归系统中的应用。当非递归系统为20阶时，通过对两种滤波器的辨识，可以看到辨识后的输出与原始系统输出的几乎一致，并且权系数值也几乎相等。

通过本文分析，可以看到SER在系统辨识应用中能得到较好的辨识结果。SER算法相对LMS算法能有较快的收敛速度，但是其算法的复杂度会高于LMS算法。当系统复杂时，SER算法就会存在数据运算量大的缺点，在收敛的实时性上难以达到较好的效果。

参考文献：

[1]胡广书.数字信号处理-理论、算法与实现[M].北京：清华大学出版社，2012.

[2]威德罗.自适应逆控制[M].西安：西安交通大学出版社，2000.

[3]沈福民.自适应信号处理[M].西安：西安电子科技大学出版社，2002.

[4]戚晓慧，吴瑛，王云龙.多带结构自适应滤波器的变步长矩阵设计[J].西安电子科技大学学报，2015，42（4）：198-204.

[5]王益根.基于LMS的自适应滤波器典型应用的MATLAB实现[J].扬州职业大学学报，2007，11（2）：35-37.

[6]吴言风，吴国正，李华.基于RLS算法的自适应逆控制系统的研究[J].海军工程大学学报，2005，17（1）：82.

[7]杨威，刘宏清，黎勇，等.冲击噪声下的LMS和RLS联合滤波算法[J].西安电子科技大学学报（自然科学版），2017，44（2）：165-170.

[8]汪潮，单家方.一种新的变步长LMS自适应滤波算法仿真及性能分析[J].科技通报，2015（1）：87-89.

【通联编辑：朱宝贵】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。