《蒙特卡洛树搜索在游戏“2048”中的运行机制分析》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

蒙特卡洛树搜索在游戏“2048”中的运行机制分析

范文

赵丹娜曾孟佳黄旭

摘要：对蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）算法在游戏“2048”中的运行机制进行了分析研究。在MCTS过程中，利用上限置信区间（Upper Confidence Bound Apply to Tree，UCT）算法计算当前局面所有可移动4个方向节点的UCT值，选择使节点价值最大的方向作为下一次的移动方向，再经过扩展、模拟阶段，直到达到游戏限制范围后进行反向传播，以当前路径的局面评估值对其父节点、祖父节点直至根节点的节点价值进行更新，以此得到最佳移动方向，进而得到最优选择策略。

关键词：MCTS；UCT；游戏“2048”

中图分类号：TP18文献标志码：A文章编号：1008-1739（2020）02-64-4

0引言

人工智能（Artificial Intelligence，AI）是长期以来的热点话题，而计算机博弈（机器博弈）是广受关注的研究方向。其中最复杂的博弈项目之一———棋类，则是充分检验其真实发展水平的重要手段。在象棋领域，1997年“深蓝”击败世界排名第一棋手，至此，标志着计算机博弈进入一个新的高度。而在难度更大的围棋领域，计算机却鲜有造诣。直到2006年蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）的提出，这一窘境才被打破[1]。之后，计算机博弈相关研究有了跨越性的发展。

MCTS是在完美信息博弈场景中进行决策的一种通用技术，不仅在围棋博弈，更是在其他游戏博弈中得到广泛应用[2-4]，其根据局面评估算法产生的结果进行不断地调整优化。2012年，一种基于MCTS并行化方法的提出，极大地提升了MCTS算法的性能[5]。在MCTS中，上限置信区间（Upper Confidence Bounds for Trees，UCT）算法是一个十分重要的算法，对节点的最大访问次数加以限制。简言之，MCTS是一种将蒙特卡洛模拟评估与UCT相结合的最优优化算法[6]。现今，MCTS被广泛应用于各类计算机围棋博弈程序中。本文以“2048”游戏为例，对MCTS算法运行机制进行了简要分析。

1游戏“2048”

1.1游戏玩法

游戏在4*4棋盘中进行，游戏开始时，计算机方在当前任意空方格里随机给出2个2，在随后的走棋过程中，玩家每走一步，计算机随机在空的方格中给出一个2或4。游戏玩家每次可以选择上、下、左、右4个行棋策略中的一种（某些格局会少于4种，因为有些方向不可走）走棋，行棋后方格中的数值按照既定逻辑移动及合并，格局完成转换[7]。移动合并规则是移动方向上若有2个相邻方格的数值相同则合并，数值更新为“原数值*2”。由于游戏玩家应对方式主观性过大，故本文只针对计算机行子方式进行判断分析。

游戏结束的判断方法有2种。第1种：玩家通过对棋盘上数字的移动，使其累加得到“2048”，则游戏结果为“胜利”；第2种：玩家对棋盘上的数字进行任意移动，若游戏中出现无效操作，格子全满，且无法向4个方向中任何一个方向移动（均不能触发合并），则游戏结束，游戏结果以游戏全过程中所合并各方格累加和的最大值为游戏最终结果。由于此时的游戏结果没有达到“2048”，因此本判断方法不产生游戏胜利的结果。

1.2游戏难点

“2048”的游戏规则看似简单，但在实际操作中，每次移动棋盘上均会随机出现数字2或4，在给游戏玩家对下一步的动作增加了不确定性的同时，也增添了一定的游戏难度。

“2048”是由玩家与计算机进行对弈的一种信息对称双人博弈模型，即在游戏过程中对弈双方获取的格局信息完全一致，故移动策略的选择对接下来的格局至关重要[8]。

游戏进行过程中，玩家尽可能避免移动数值较大的方块，因为一旦移动会导致这个游戏局面多个方块数值改变，特别是要避免出现数值较大的方格（如1 024或512）周围被小数值方格（如2或4）包围的局面。

2“2048”中MCTS算法的应用

2.1 MCTS

MCTS是在树搜索的其中某个节点上，从当前位置逐步向下延伸搜索，遇到未完全展開的节点时，则进行单次模拟，即将该节点作为单次模拟的根节点，继续向下延伸搜索，直到因时间或其他限制因素而停止，并将搜索结果反向传播回当前根节点，更新其评估值及访问次数，从而获得该节点的优劣信息做出决策。在实验条件不变的情况下重复实验，实验次数越多，误差越小，评估值将越准确[9]。MCTS其实是一种对模拟结果进行不断反馈调整的启发式搜索算法[10]，搜索流程如图1所示。

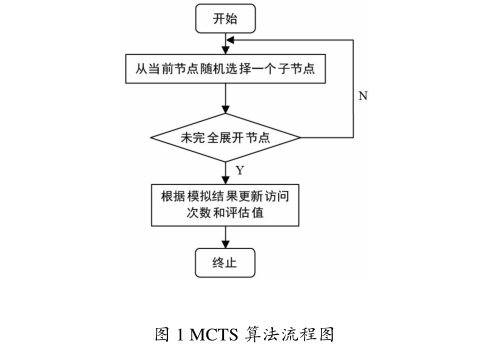
MCTS算法能够从模拟产生结果的优劣去思考、学习如何提高下一次策略的质量，并通过多次随机模拟后得到的评估值来判断每一个节点的优劣，从而选择最佳路径。算法执行过程一般分为路径选择、扩展、模拟和反向传播4个阶段。

2.2应用

（1）选择

从根节点开始选择最优的子节点，直到达到叶子节点，即选择最具搜索潜力的路径，这里节点选择算法采用UCT算法。置信区间表示的是一个统计上的计算值，是在所有可能的下一节点中选择任一节点，随机模拟至游戏结束，并将最终值作为返回值（节点价值），以此类推，然后在节点中选择节点价值最高的节点作为下一次的选择节点[11-13]。如果当前选择的最优子步骤在之后的模拟中多次失败，则该值变小，从而使另一个同级的子步骤变得更优，因此在选择过程中会减少搜索的广度，从而减少系统资源的浪费[14]。路径选择的实质是节点的选择，即根据节点价值在每一步选择当前的最优节点，搜索路径上的所有最优节点组成最优路径。使用UCT算法进行搜索树树内选择，其公式为：

假定值保持不变，根据式（1），访问次数越小，式（1）的第2项值越小，则的值越大，认为当前节点是有价值的节点；相反，访问次数越多，的值越小，则算法会偏向于去寻找访问次数越小的节点。但在实际过程中的值会变。

在游戏“2048”中使用MCTS算法的过程是以当前局面为节点，在上下左右任一方向的移动及UCT值计算过程分别执行100次[15]，进行移动模拟操作，结束后记录每一次移动得分，并对每一个方向最终结果取平均值，并将4个值做大小比较，选取最大值对应的方向作为最佳移动方向。这里循环100次的选择主要从计算的角度考虑，若次数太少，得到的UCT值可能分布较稀疏，不能得到搜索过程的全局表现；若次数过大，则计算与搜索过程的复杂度均会增加，加大系统资源开销。算法流程如图2所示。

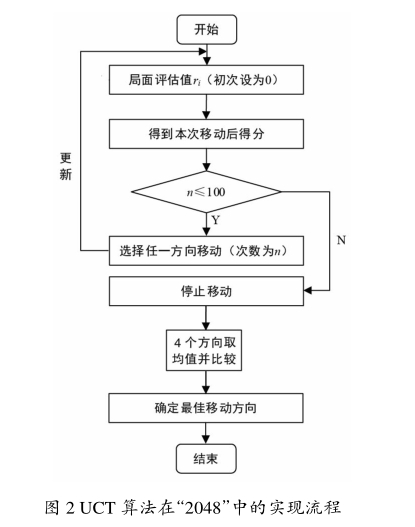
在游戏“2048”中，上下左右选择任一方向进行移动，每一次移动操作后更新当前局面评估值直至操作满100次，得到当前最优方向，该方向即为当前情况下的最优节点。UCT算法在游戏中的优势在于能够平衡探测和利用之间的关系，因为在实际情况中由于操作的随机性，往往会存在节点价值最高而实际收益不高的情况。

（2）扩展

若当前节点为非完全展开节点，则将其作为根节点，继续向下创建一个或者多个子节点（每次移动后的局面都看成是一个节点），选择其中一个，即只有在当前获得的统计结果不足以计算出下一个节点时，随机选择一个子节点。故在节点的扩展过程中，搜索树会逐渐扩充。而在“2048”中，根据当前节点继续在上下左右4个方向进行移动选择。

（3）模拟

从当前节点开始模拟接下来可能出现的结果，一直循环多次，直到游戏结束。游戏中，不同的方向不仅会导致棋子个数的不同，更重要的是要考虑到棋子及其周围棋子所代表的数字，如果移动后棋子周围的棋子数值远大于该棋子，则这种移动并非最优策略。因此在实际操作中，应尽可能的减少方块的个数，尽量把棋子往合并数目越多的那一个方向移动，同理也就增加了局面评估值[16]。游戏“2048”的蒙特卡洛树拓展过程模拟如图3所示。

（4）反向传播

在模拟过程结束即棋子在棋盘上无法移动时，将该搜索树其中一个叶节点的评估值反向更新该节点的父节点及其祖先节点等的价值，即游戏在某一方向移动结束后，从末到首反向移动，更新各节点的访问次数（移动某一方向的次数），从中得出节点的访问次数和节点的评估值。

3应用分析

游戏“2048”走棋过程模拟如图4所示。

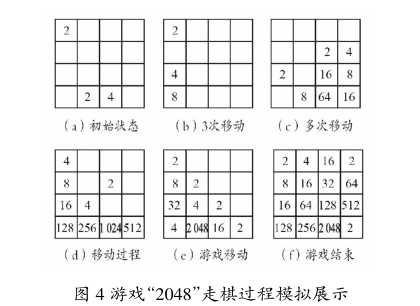
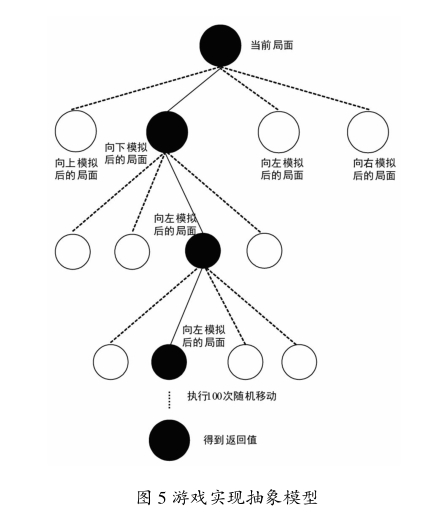
从图4所列举的6种游戏过程状态可以看出，在游戏中会尽量把数字大的方块（棋子）固定在一边，这样是为了减少游戏中大数字方块的移动，避免大量出现数字无法合并的情况。抽象模型如图5所示。

游戏中，使用UCT算法对节点的4个方向依次进行选择、扩展和模拟，在节点价值和实际收益间选择最优节点（最佳移动方向），对本次移动后进行下一步移动方向模拟，以此类推，直至局面无法再移动，此后，自叶节点（最后一次移动后的局面评估值）至根节点（此时设为0）进行反向传播，从而找出最优路径，也就是游戏“2 048”中的每一次局面最佳移动方向。

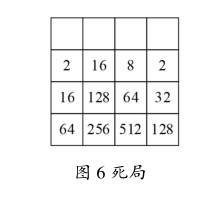
当出现以下局面时，可以稱之为死局。发生死局时，玩家没有别的选择只能向上移动，由于只有唯一路径可以选择，因此玩家失败的机率也会增加。死局示意图如图6所示。

4结束语

本文主要分析了MCTS在游戏“2048”中的运行机制。通过设置上下左右任一方向模拟随机移动100次，对每一次取得的值累加后取平均，各得到4个方向的局面评估值，由此选择当前最佳移动方向。仍存在的难点是由于游戏的每一步不仅要选择最佳移动方向，还要考虑到数字的合并情况、数字之间倍数的联系关系等，需要进行下一步的研究。

参考文献

[1] COULOM R. Efficient Selectivity and Backup Operators in Monte-carlo Tree Search[C]//Proc of the 5th International Conference on Computers and Games，Turin，Italy，2007（4630）： 72-83.

[2]林云川.基于深度学习和蒙特卡洛树搜索的围棋博弈研究[D].哈尔滨：哈尔滨工业大学， 2017.

[3]刘雅靖.基于Alpha Beta搜索算法的计算机博弈的研究与实现[D].大连：大连交通大学， 2012.

[4]许子明.一种2048游戏自动“玩游戏”算法的实现[J].科技风，2018（16）：4.

[5]季辉，丁泽军.双人博弈问题中的蒙特卡洛树搜索算法的改进[J].计算机科学，2018，45（1）：140-143.

[6] GRAF T，LORENZ U，PLATZNER M，et al.Parallel Monte-Carlo Tree Search for HPC systems[C]//Proc of the 17th International Conference on Parallel Processing， Bordeaux，France， 2011： 365-376.

[7]于永波.基于蒙特卡洛树搜索的计算机围棋博弈研究[D].大连：大连海事大学， 2015.

[8]何璇.计算机博弈在<2048>游戏的研究与应用[D].长沙：湖南师范大学，2015.

[9]刘宇.Monte carlo方法在计算机围棋中的应用[D].成都：电子科技大学，2012.

[10] BRODERICK A，RYAN B H，PHILIP H. Monte Carlo Tree Search in Hex[J].ICGA Journal，2010，4（2）：251-257.

[11]邓超，吴霖，陈磊，等.局部UCT算法在围棋死活题上的性能测试[J].信息技术，2013，37（3）：23-27.

[12]张玉琪.基于静态评估的计算机围棋UCT算法改进研究[D].南昌：南昌航空大學，2015.

[13]孙若莹，宫义山，赵刚.一种新的博弈树迭代向前剪枝搜索[J].沈阳工业大学学报，2017，39（3）：305-310.

[14]周明明，高航，赵国安.UCT算法在计算机围棋中的应用与改进[J].数据采集与处理，2012，27（S2）：330-335.

[15]胡辰坤.基于Cocos2d-x引擎的手机游戏2048及其AI的设计与实现[D].武汉：华中科技大学， 2015.

[16]刘子正，卢超，张瑞友.基于蒙特卡罗树搜索的“2048”游戏优化算法[J].控制工程，2016，23（4）：550-555.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。