陈雨桐
摘要:大数据时代,对海量数据的高效处理极为重要。集成学习算法中的随机森林和梯度提升决策树是近些年来常被用于处理数据分类与回归的方法,决策树则是随机森林和梯度提升决策树算法组成的基础。本文首先对决策树进行了介绍,然后分别对随机森林和梯度提升决策树进行了分析,叙述了两种算法的优缺点以及近几年来在生活生产中的应用,并对两种算法进行了比较。
关键词:决策树;随机森林;梯度提升决策树;集成学习
中图分类号:TP311? ? ? 文献标识码:A
文章编号:1009-3044(2021)15-0032-03
随着科技的不断进步与发展,海量的数据涌入人们的生活,人们便希望可以有方式能够高效地处理这些数据。于是,产生了数据挖掘技术。决策树便是数据挖掘技术中典型的算法,决策树可以处理分类问题和回归问题,但它属于单个的分类器,具有容易发生过拟合现象的缺陷。因此,集成学习算法应运而生。其中,随机森林和梯度提升决策树是两种由多棵决策树集合而成的算法,且它们在集成学习算法中很具有代表性。本文将对随机森林算法和梯度提升决策树算法进行综述。
1决策树
1.1决策树简介
决策树是机器学习中一类用于分类和回归的算法,目前常用的决策树算法主要有在1986年由Quinlan提出的ID3算法、由ID3算法改进形成的C4.5算法、进一步改进形成的C5.0算法和在1984年由Breiman提出的CART算法。决策树的理论结构是一个树状图,图中每个非叶子节点代表一种决策,每一个分支代表一种决策结果,每一个叶子节点代表一个类别。决策树分类的方法就是从根结点开始,对某个输入实例进行决策,每次决策都根据测试结果,通过分支将实例流向下一个节点,直至此实例被划分到一个叶结点,其便被分到了此叶结点所代表的类中。
决策树的构造过程依据训练集特征的决定性,将决定性最重要的特征作为根节点,之后依次按照特征决定性的重要程度分出子节点,直至最后生成叶结点所代表的类。因此,在决策树的构建过程中,关键是找出每次在当前分支节点起决定性作用最大的特征,使最后分出的类尽可能“纯”,不同的决策树算法评估纯度差和选择特征的方式不同[1],ID3算法使用信息增益选择特征,C4.5和C5.0算法使用信息增益率进行选择,而CART算法使用Gini指数判断和选择特征。
1.2优势和缺陷
决策树的优势是树状图便于理解,能很好地展现出样本的分类过程和分类过程中属性的重要程度,且决策树既能够处理连续型数据,又能够处理离散型数据。但同时,决策树也存在着一些缺陷,一个最典型的缺陷是通过决策树算法进行分类操作,很容易出现对训练数据集分类效果很好,但对测试数据集分类效果较差,即出现过拟合[1],无法有效地对所有新样本进行分类,泛化能力弱。于是,便出现了对决策樹进行剪枝[1]的方法,减去不必过度细化的分支,以此来避免发生过拟合现象。但剪枝的方式只能在一定程度上优化决策树,当数据庞大复杂时,应用决策树依旧有一定限制。因此,便出现了基于决策树的集成学习算法,对数据分类问题有更好的可行性。
2随机森林
2.1随机森林简介
随机森林(Random Forest)是一种基于决策树的集成学习算法,它由多棵决策树组成,每棵决策树具有一个投票权,随机森林最后的分类结果就取决于这些决策树的投票结果。随机森林中每棵决策树的生成方式如下:
(1)从训练集中用有放回抽样法随机抽取一定数量的样本组成新训练集;
(2)在特征集中随机选择一定数量的特征;
(3)利用建立决策树的方法,依次计算最优的特征作为当前节点进行建树。
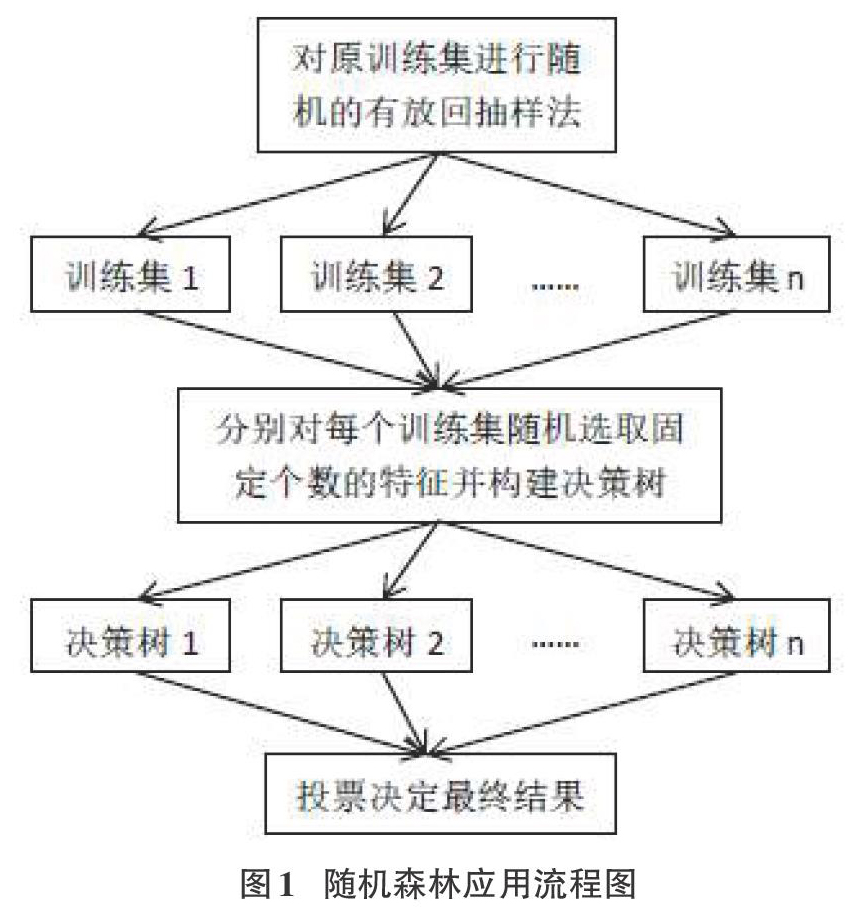
上述过程重复执行n次,每次抽取的样本数量、特征数量都固定不变,建立的n棵树就组成了随机森林。由于每次对样本和特征都是随机抽取,就会构造出许多不同的决策树。因此,随机森林中的所有决策树对同一个样本进行分类,会得到许多分类结果,每棵决策树对其分类结果进行一次投票,通常取被投次数最多的类作为该样本所属的类。用一个简单的流程图表示随机森林应用的过程,如下所示:
由于随机森林选取训练样本和特征的随机性,以及多次对测试样本进行分类的特性,应用此算法进行分类可以较好地解决单棵决策树泛化能力弱的问题,一定程度上弥补了决策树容易出现过拟合的缺陷。
2.2优缺点
随机森林主要有以下优点:
(1)实现较为简单,且训练速度快。
(2)可以处理多特征的数据,适应能力强。
(3)采用了集成算法后分类精度比单个算法要高。
(4)不容易发生过拟合,泛化能力强。
(5)对不平衡的数据集,随机森林可以平衡误差[2]。
但随机森林算法也存在着一定的缺点,在一些噪声比较大,即错误数据较多的分类问题或回归问题中,随机森林也会出现过拟合;对于有不同特征的数据,可能会出现建立了多棵相似决策树的情形,对分类的真实结果产生一定偏差。
2.3应用
由于随机森林算法性能较好,目前在许多领域都有所应用。例如,彭远新等人[3]利用随机森林算法在潍北平原进行土壤全氮高光谱估算,因为获取土壤的氮素信息对植物生长极为重要;李锐光等人[4]改进了随机森林算法,将其用于物联网设备流量分类,对网络空间的流量管理有重要意义;萧伊等人[5]将随机森林应用于分析膝关节炎患者结构特征和症状定量,为在膝关节的相关症状评估以及治疗指导贡献了帮助。可见,随机森林作为近些年来热门的应用算法,在各行各业中充分发挥了其可用之处。
3梯度提升决策树
3.1梯度提升决策树简介
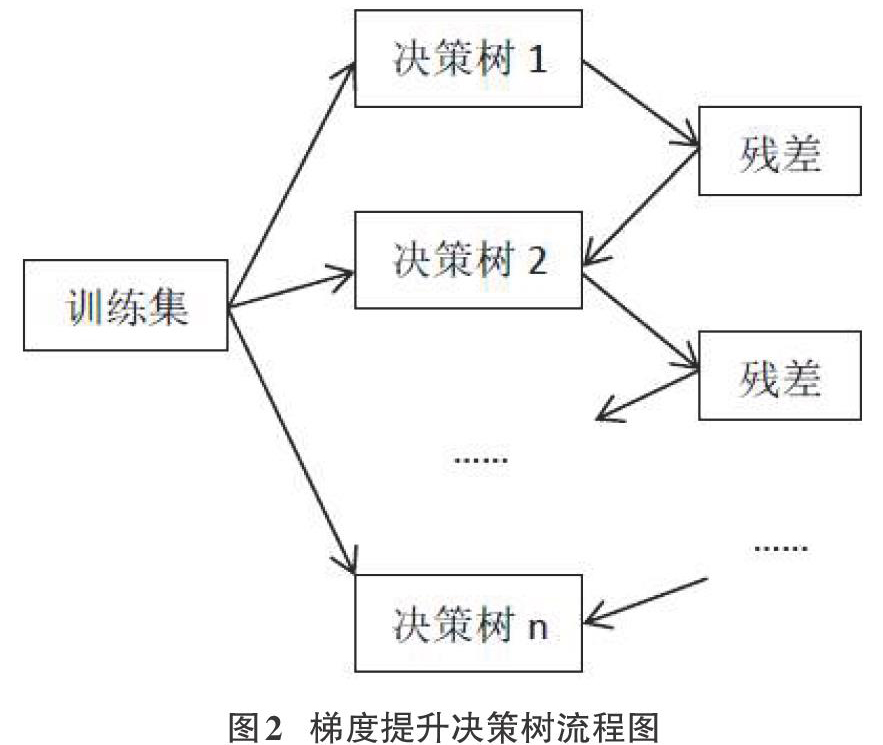
GBDT(Gradient Boosting Decision Tress),称作梯度提升决策树,是决策树集成学习算法中的一种迭代算法,由多棵依据原训练集构造的决策树组成,进行多次迭代,每次迭代在一棵决策树中产生一个结果,下一棵决策树在上一次的残差(真实值-预测值)基础上进行训练,经过所有决策树后,生成最终的结果。梯度提升决策树算法的过程如下图所示:
样本每经过一棵决策树,它所预测的结果会与真实结果有一定的差异。每棵新的决策树建立的目的是使残差在梯度[6]方向上减少,以此最终预测出最接近真实结果的数据。
为了更好地方便理解梯度提升决策树的拟合数据的过程,下面以一个简单的例子进行演示:
假设有个人身高170cm,我们最初用160cm去拟合,发现残差为10cm,接下来我们用7cm去拟合上一轮的残差,此时的残差为3cm,第三次我们用2cm去拟合,此时还有1cm的差距,可以继续不断地迭代直至GBDT中的迭代次数使用完毕,我们会发现每次迭代拟合的差值都会减小,且每次迭代后预测值都会更加逼近真实值,这就是梯度提升决策树的简单应用。
3.2优缺点
梯度提升决策树主要有以下优点:
(1)几乎可以适用于所有的回归问题,无论是线性回归还是非线性回归。
(2)预测精度高,泛化能力强。
(3)可以灵活处理连续型数据和离散型数据。
同时,梯度提升决策树也存在着一定的缺点,由于其决策树是依次迭代对数据进行训练的,即决策树间存在依赖关系,导致梯度提升决策树难以并行训练数据。
3.3应用
梯度提升决策树是人们现在解决许多数据问题能够用到的算法。例如,路志英等人[7]将改进的GBDT模型用于对天津强对流灾害的预报,陈涛等人[8]将GBDT模型用于滑坡易发性的评价中,并证实了GBDT模型在此问题中具有比较高的预测能力,近些年来还有许多关于GBDT的应用,可见其应用效果良好。
4 随机森林与梯度提升决策树的比较
随机森林和梯度提升决策树都属于集成学习算法,它们都由多棵决策树所组成,最终的结果也需要经过所有决策树共同决定。但随机森林与梯度提升决策树在思想和算法上有所区别,随机森林采用的是机器学习中的Bagging[9]思想,而梯度提升决策树则采用的是Boosting[10]思想。Bagging和Boosting都是集成学习方法,且都是通过结合多个弱学习器并提升为强学习器来完成训练任务。Bagging通过有放回均匀抽样法从训练集中抽取样本训练弱分类器,每个分类器的训练集是相互独立的,而Boosting的每个分类器的训练集不是相互独立的,每个弱分类器的训练集都是在上一个弱分类器的结果上进行取样。由于随机森林采用了Bagging思想,那么决策树训练集相互独立,组成随机森林的树相互之间可以并行生成,而梯度提升决策树采用的Boosting思想,组成的树需要按顺序串行生成。并且随机森林中的决策树对训练集进行训练时,对所有的训练集一视同仁,而梯度提升决策树对不同的决策树依据重要性赋有不同的权值[6]。在应用上,随机森林与梯度提升决策树都可以解决分类与回归问题,但随机森林更多地用于解决分类问题,梯度提升决策树则更多用于处理回归问题。
5结束语
随机森林和梯度提升决策树都是集成算法中的经典算法,目前在许多领域都有所应用,也有一些科研者将随机森林或梯度提升决策树与其他方法相结合,形成复合算法去研究、处理相应问题。虽然目前这两种算法应用广泛,但仍有缺陷存在,如何更好地对其更新与拓展是非常值得我们思考和研究的事情,这样才能更灵活、更有效地让其应用于人们的生活和生产中。
参考文献:
[1] 周志华.机器学习[M].北京:清华大学出版社,2016.
[2] 曹正凤.随机森林算法优化研究[D].北京:首都经济贸易大学,2014.
[3] 彭远新,蒙永辉,徐夕博,等.基于随机森林算法的潍北平原土壤全氮高光谱估算[J].安全与环境学报,2020,20(5):1975-1983.
[4]李锐光,段鹏宇,沈蒙,等.基于随机森林的物联网设备流量分类算法[EB/OL].(2020-10-20).北京航空航天大学学报:1-9.
[5] 萧伊,肖峰,徐海波.随机森林模型在膝关节炎患者结构特征与症状定量分析中的应用[J].磁共振成像,2020,11(10):877-884.
[6]Jerome H. Friedman. Greedy function approximation: A gradient boosting machine[J]. The Annals of Statistics,2001,29(5).
[7] 路志英,汪永清,孙晓磊,等.基于Focal Loss改进的GBDT模型對天津强对流灾害的预报[J].灾害学,2020,35(3):34-37,50.
[8] 陈涛,朱丽,牛瑞卿.基于GBDT模型的滑坡易发性评价[C]//第五届高分辨率对地观测学术年会论文集.西安,2018:511-520.
[9] Breiman L.Bagging predictors[J].Machine Learning,1996,24(2):123-140.
[10] Freund Y,Schapire R E.A decision-theoretic generalization of on-line learning and an application to boosting[J].Journal of Computer and System Sciences,1997,55(1):119-139.
【通联编辑:唐一东】
- FSSC 22000食品安全体系认证新版本V5的变化浅谈
- 食品无小事,安全挂心间
- 好时推出酸甜苦辣系列高端新品,吸引消费者眼球
- 科莱恩在2019国际橡塑展期间举办客户研讨会,重点展示卓越服务和创新性母粒解决方案
- 益生元菊苣根纤维有助于保持儿童在抗生素治疗后的肠道微生物平衡
- 浙江省启动食品安全宣传周活动
- 骄阳似火难阻民众热情,众志成城共筑食安防线
- 活力创新成就持续增长典范,2020 SIAL China中食展20周年全新启航
- IFFA 2019圆满落幕,传统工艺联动高新技术碰撞新火花
- 两种不同陈醋挥发性成分分析及研究
- 餐饮食品安全控制课程教学体系的探讨
- 超高效液相色谱-串联质谱法测定鸡肉中羟基甲硝唑和羟甲基甲硝咪唑残留量
- “食品安全检验技术”课程教学改革的探索
- 一起家庭集体聚餐食物中毒事件的原因分析与对策
- 浅谈县级食品检测中心如何服务食品安全
- 从肠道健康到国民营养,蒙牛展现大健康战略
- 取自天然的配料产品,助力运动型营养新突破
- 定格“靓丽”、“锁住”营养,让新鲜更长久
- 借助“一物一码”,打造“以消费者为中心”的生态圈
- 食品中微生物污染分析及其检测技术
- 专业做产品、专注做服务,美正集团为食品安全行业贡献力量
- 岛津LabSolutions:实现网络时代创新性分析操作环境下的信息安全与管理
- 沃尔玛食品安全创新平台第三期项目征集正式启动——着力提升供应链的洞察力和透明度
- 依案说法——浅论食用农产品的定性及标签规定
- 食品生产企业用工方面需要注意哪些事项?
- inscribableness
- inscribablenesses
- butlerlike
- butlers
- butlership
- butlerships
- buts
- but's
- butt
- butted
- butter
- buttercup
- buttercupped
- buttercuppy
- buttercups
- buttered
- butterer
- butterers
- butterflied
- butterflies
- butterfly
- butterflying
- butterflylike
- buttering
- butterless
- 寒云
- 寒人
- 寒从脚下起
- 寒从脚底来
- 寒从足起,病从口入
- 寒伧
- 寒促
- 寒假
- 寒儒
- 寒儒薄相
- 寒光
- 寒光闪闪的戟
- 寒光闪闪的样子
- 寒兔
- 寒具
- 寒冬
- 寒冬时树木的枝条
- 寒冬时的鸟
- 寒冬时节
- 寒冬暑夏
- 寒冬的太阳
- 寒冬的电扇
- 寒冬腊月
- 寒冬腊月倒开花
- 寒冬腊月十冬腊月