网站首页  词典首页

请输入您要查询的论文：

　

标题 基于Sobel的多方向算子模板边缘检测算法
范文 沈德海+侯建+鄂旭+张龙昌


摘 要： 针对传统Sobel算子存在的边缘检测方向性不强及提取边缘较粗等问题，提出了一种改进的多方向算子模板的边缘检测算法。算法增加了22.5°， 45°，67.5°，112.5°，135°和157.5°六个方向算子模板，能够较好地检测出图像不同的方向边缘。模板权值根据中心像素点到邻域像素的距离及方向夹角的大小进行设定，充分考虑到了邻域内像素对中心点方向梯度的贡献大小；算法对梯度图像采用了改进的非极大值抑制方法进行细化，得到了较细的图像边缘。实验结果表明，与传统Sobel算法相比，该算法提取的边缘图像具有边缘方向性强且边缘较细的优点，具有较高的应用价值。
关键词： 边缘检测； 多方向算子模板； 非极大值抑制； 梯度图像细化
中图分类号： TN919?34； TP391.41 文献标识码： A 文章编号： 1004?373X（2015）04?0091?03
0 引 言
边缘检测是图像处理与计算机视觉等领域中的一个关键技术，是一个图像预处理过程，其结果的好坏将直接影响着图像特征提取、图像分割、图像识别等后续处理的精度和效果。传统的边缘检测算法有Roberts[1]、Sobel[2]、Prewitt[3]、Log[4]、Kirsch[5]等，它们通过算子模板与图像进行卷积运算，获取图像梯度，通过阈值对边缘进行提取。这些算法在抗噪性能、边缘定位精度及细化程度难以满足实际需求。近年来，一些学者将新的理论应用到边缘检测中，提出一些新的算法，如小波算法 [6]、形态学算法 [7]、模糊理论算法[8]、遗传算法[9] 、蚁群算法[10]等，这些算法在边缘精度、抑噪性能等方面有着一定的优势，但也各自存在着诸如计算量大、算法复杂、适应性差等一些问题。本文在统Sobel算法基础上，提出一种多方向算子模板的边缘检测算法，算法采用0°，22.5°，45°，67.5°，90°，112.5°，135°和157.5°八个方向的算子模板来计算图像梯度，并采用非极大值抑制方法对梯度图像进行细化，使得提取的图像边缘方向性较强，连续性较好，边缘宽度小。
1 传统Sobel算子原理
图像边缘主要包括幅度和方向两个属性，沿着垂直边缘的方向，像素灰度值的变化较为剧烈。在边缘区域，通常用导数算子进行检测，其中一阶导数最大值处对应边缘位置，二阶微分过零点处对应边缘位置。边缘是图像灰度值发生显著变化的区域，该区域点的梯度值较大，对应的一阶导数也较大。所以可将梯度值大于的某一阈值的点当作边缘点，即可得到边缘图像。设u（x，y）为数字图像函数，其在点（x，y）处的梯度可以定义为下列向量：
[u（x，y）=?f?x，?f?yT=[Gx，Gy]T] （1）
幅值和方向分别为如式（2） 和式（3）所示。
[Δu（x，y）=G2x+G2y] （2）
[θ=arctanGxGy] （3）
式（2）的梯度幅值可以采用式（4）或式（5）简化计算。
[Δu（x，y）=max（Δux，Δuy）] （4）
[Δu（x，y）=Δux+Δuy] （5）
式中Δux和Δuy为一阶导数，可以用一阶微分代替。
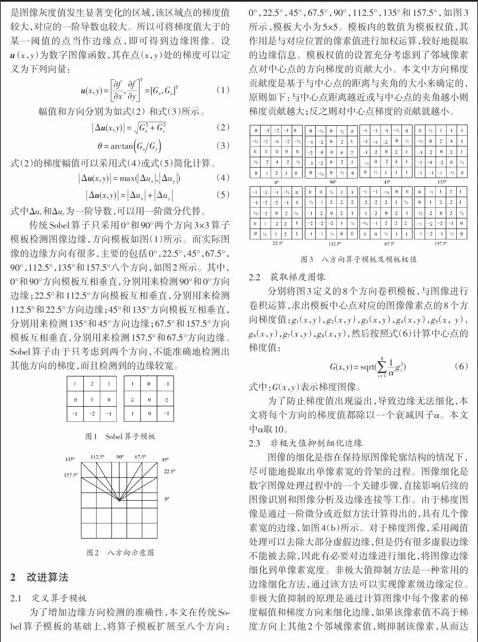
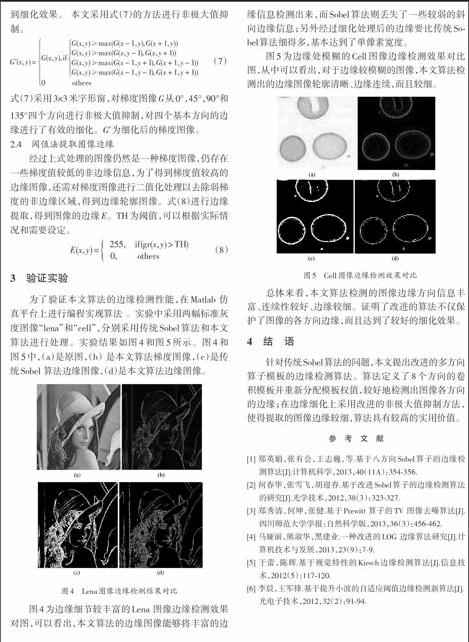
传统Sobel算子只采用0°和90°两个方向3×3算子模板检测图像边缘，方向模板如图（1）所示。而实际图像的边缘方向有很多，主要的包括0°，22.5°，45°，67.5°，90°，112.5°，135°和157.5°八个方向，如图2所示。其中，0°和90°方向模板互相垂直，分别用来检测90°和0°方向边缘；22.5°和112.5°方向模板互相垂直，分别用来检测112.5°和22.5°方向边缘；45°和135°方向模板互相垂直，分别用来检测135°和45°方向边缘；67.5°和157.5°方向模板互相垂直，分别用来检测157.5°和67.5°方向边缘。Sobel算子由于只考虑到两个方向，不能准确地检测出其他方向的梯度，而且检测到的边缘较宽。
2 改进算法
2.1 定义算子模板
为了增加边缘方向检测的准确性，本文在传统Sobel算子模板的基础上，将算子模板扩展至八个方向：0°，22.5°，45°，67.5°，90°，112.5°，135°和157.5°，如图3所示，模板大小为5×5。模板内的数值为模板权值，其作用是与对应位置的像素值进行加权运算，较好地提取的边缘信息。模板权值的设置充分考虑到了邻域像素点对中心点的方向梯度的贡献大小。本文中方向梯度贡献度是基于与中心点的距离与夹角的大小来确定的，原则如下：与中心点距离越近或与中心点的夹角越小则梯度贡献越大；反之则对中心点梯度的贡献就越小。
2.2 获取梯度图像
分别将图3定义的8个方向卷积模板，与图像进行卷积运算，求出模板中心点对应的图像像素点的8个方向梯度值：g1（x，y），g2（x，y），g3（x，y），g4（x，y），g5（x， y），g6（x，y），g7（x，y），g8（x，y），然后按照式（6）计算中心点的梯度值：
[G（x，y）=sqrt（i=181αg2i）] （6）
式中：G（x，y）表示梯度图像。
为了防止梯度值出现溢出，导致边缘无法细化，本文将每个方向的梯度值都除以一个衰减因子α。本文中α取10。
2.3 非极大值抑制细化边缘
图像的细化是指在保持原图像轮廓结构的情况下，尽可能地提取出单像素宽的骨架的过程。图像细化是数字图像处理过程中的一个关键步骤，直接影响后续的图像识别和图像分析及边缘连接等工作。由于梯度图像是通过一阶微分或近似方法计算得出的，具有几个像素宽的边缘，如图4（b）所示。对于梯度图像，采用阈值处理可以去除大部分虚假边缘，但是仍有很多虚假边缘不能被去除，因此有必要对边缘进行细化，将图像边缘细化到单像素宽度。非极大值抑制方法是一种常用的边缘细化方法，通过该方法可以实现像素级边缘定位。非极大值抑制的原理是通过计算图像中每个像素的梯度幅值和梯度方向来细化边缘，如果该像素值不高于梯度方向上其他2个邻域像素值，则抑制该像素，从而达到细化效果。 本文采用式（7）的方法进行非极大值抑制。

[G′（x，y）=G（x，y），ifG（x，y）≥max（G（x-1，y），G（x+1，y）） G（x，y）≥max（G（x，y-1），G（x，y+1）） G（x，y）≥max（G（x-1，y+1），G（x+1，y-1））G（x，y）≥max（G（x-1，y-1），G（x+1，y+1）） 0 others] （7）
式（7）采用3×3米字形窗，对梯度图像G从0°，45°，90°和135°四个方向进行非极大值抑制，对四个基本方向的边缘进行了有效的细化。G′为细化后的梯度图像。
2.4 阈值法提取图像边缘
经过上式处理的图像仍然是一种梯度图像，仍存在一些梯度值较低的非边缘信息，为了得到梯度值较高的边缘图像，还需对梯度图像进行二值化处理以去除弱梯度的非边缘区域，得到边缘轮廓图像。式（8）进行边缘提取，得到图像的边缘E。TH为阈值，可以根据实际情况和需要设定。
[ E（x，y）= 255， if（gr（x，y）>TH） 0， others] （8）
3 验证实验
为了验证本文算法的边缘检测性能，在Matlab 仿真平台上进行编程实现算法 。实验中采用两幅标准灰度图像“lena”和“cell”，分别采用传统Sobel算法和本文算法进行处理。实验结果如图4和图5所示。图4和图5中，（a）是原图，（b） 是本文算法梯度图像，（c）是传统Sobel 算法边缘图像，（d）是本文算法边缘图像。
图4为边缘细节较丰富的Lena 图像边缘检测效果对图，可以看出，本文算法的边缘图像能够将丰富的边缘信息检测出来，而Sobel算法则丢失了一些较弱的斜向边缘信息；另外经过细化处理后的边缘要比传统Sobel算法细得多，基本达到了单像素宽度。
图5为边缘处模糊的Cell图像边缘检测效果对比图，从中可以看出，对于边缘较模糊的图像，本文算法检测出的边缘图像轮廓清晰、边缘连续，而且较细。
总体来看，本文算法检测的图像边缘方向信息丰富、连续性较好、边缘较细。证明了改进的算法不仅保护了图像的各方向边缘，而且达到了较好的细化效果。
4 结 语
针对传统Sobel算法的问题，本文提出改进的多方向算子模板的边缘检测算法。算法定义了8个方向的卷积模板并重新分配模板权值，较好地检测出图像各方向的边缘；在边缘细化上采用改进的非极大值抑制方法，使得提取的图像边缘较细，算法具有较高的实用价值。
参考文献
[1] 郑英娟，张有会，王志巍，等.基于八方向Sobel算子的边缘检测算法[J].计算机科学，2013，40（11A）：354?356.
[2] 何春华，张雪飞，胡迎春.基于改进Sobel算子的边缘检测算法的研究[J].光学技术，2012，38（3）：323?327.
[3] 郑秀清，何坤，张健.基于Prewitt 算子的TV 图像去噪算法[J].四川师范大学学报：自然科学版，2013，36（3）：456?462.
[4] 马娅丽，熊淑华，黑建业.一种改进的LOG 边缘算法研究[J].计算机技术与发展，2013，23（9）：7?9.
[5] 于蕾，陈辉.基于视觉特性的Kirsch边缘检测算法[J].信息技术，2012（5）：117?120.
[6] 李晨，王军锋.基于提升小波的自适应阈值边缘检测新算法[J].
光电子技术，2012，32（2）：91?94.
[7] 黄海龙，王宏.一种基于小波变换和数学形态学的边缘检测算法[J].东北大学学报：自然科学版，2011，32（9）：1315?1318.
[8] 潘花.一种基于模糊理论的图像边缘检测算法[J].重庆工商大学学报：自然科学版，2013，30（7）：53?56.
[9] 吴晓琳，张东.基于遗传算法实现数字图像边缘检测[J].舰船电子工程，2011，31（9）：117?118.
[10] 刘坤岭，周新志.基于均衡化和K均值改进蚁群算法的边缘检测[J].计算机仿真，2011，28（1）：285?288.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/6 6:56:22