网站首页  词典首页

请输入您要查询的论文：

　

标题 认知无线电中基于支持向量机的频谱空闲度预测
范文 李红岩



摘 要： 研究认知无线系统中的频谱小时空闲度预测问题，针对GSM系统的载频小时空闲度时间序列的非线性特点，提出一种基于支持向量机的预测模型构建方法。为提高模型的预测精度，在GSM系统小时空闲度时间序列特征分析的基础上，利用序列的节假日特性和日周期特性，对数据序列进行了重构。仿真结果表明，与采用基于神经网络的预测模型相比，该预测方法对工作日和周末均具有较高的预测精度， 其预测绝对百分比误差在4以内。
关键词： 支持向量机； 频谱预测； 认知无线电； 神经网络
中图分类号： TN911?34 文献标识码： A 文章编号： 1004?373X（2015）07?0019?04
0 引 言
在当前频谱资源供需矛盾日益突出的背景下，认知无线电[1]因其提高频谱利用率的巨大潜力而受到研究者的广泛关注。认知无线电得以应用的必要前提是保证授权系统对频谱的优先使用权，因而它所使用的频谱随着授权用户用频行为的变化呈现出移动特征。频谱移动一方面增加了认知无线电无线资源管理的复杂度，另一方面也使得时延敏感性业务的服务质量难以得到有效保障。频谱移动性管理是认知无线电面临的技术难题之一。对未来时段频谱空闲度的准确预测能够为认知无线电的频谱移动性管理和决策提供更有效的信息支持，降低频谱移动带来的负面影响，增强认知系统的可靠性和频谱利用率等整体性能[2?4]。因此，基于频谱使用状态的历史数据，研究认知无线电频谱预测机制，对认知无线电的最终实现和推广具有重要意义。
目前，已有的频谱预测机制多是基于时隙通信模式，将每个时隙的频谱占用或空闲情况建模为一个二元时间序列[5]，采用ARIMA模型[6]、神经网络模型[7]和马尔可夫链模型[8]对二元时间序列进行预测。其中，ARIMA模型适合预测平稳时间序列，而频谱状态时间序列是一个有人参与的受多种因素影响的复杂系统，属于非平稳非线性时间序列，因此将其应用于频谱预测的效果不理想，预测精度较低[6]；神经网络模型需要大量训练数据才能实现高精度的预测，且由于神经网络在理论上固有的缺陷而容易在模型训练时出现过学习和泛化能力弱的问题。马尔可夫链预测模型的精度取决于转移概率矩阵的可靠性，因此该预测模型要求足够多、足够准确的统计数据对系统转移概率进行测定，才能保证预测精度。
综上所述，频谱预测对认知无线电系统性能的有效保障起到重要作用。目前已有研究对频谱预测模型和机制的探讨尚不够充分，频谱状态时间序列的取值间隔多以时隙为单位，序列的可预测较低，预测精度有待提高。考虑到认知系统中网络层协议需要较大时间尺度的频谱信息（如未来一小时的频谱空闲度），以实现端到端的有效路由，并提高时延敏感性业务的服务质量，本文提出一种GSM系统的载频小时空闲度预测方法，鉴于支持向量机在非线性时间序列预测中的突出优势 [9]，采用支持向量机回归方法，构建高精度的载频小时空闲度预测模型。
1 支持向量回归原理
应用支持向量机进行回归预测的基本原理是，通过非线性映射[Φ]将样本从原空间映射到高维特征空间[G]中，在高维空间进行数据的线性回归和拟合。假设用于训练的样本数据集合为[{xi，yi}，]其中[xi∈Rm，][yi∈R，][i=1，2，…，][s；][s]为样本数。在高维空间中构造如下最优线性回归函数：
[y=f（x）=（ω?Φ（x））+bΦ：Rm→G，ω∈G] （1）
式中： [ω]为权向量，[ω∈Rw，][b∈R。]根据结构风险最小化准则，该最优线性回归问题可以描述为以下约束优化问题：
[minQ=12ω2+Ci=1n（ξi*+ξi）s.t. yi-（ω?Φ（xi））-b≤ε+ξi*，ω?Φ（xi）+b-yi=ε+ξi，ξi*，ξi≥0， i=1，2，…，s] （2）
式中：[C]为正则化参数，作为惩罚因子实现经验风险和置信范围的平衡折中，其值越大对数据的拟合程度越高；[ξi*，ξi]为松弛因子；[ε]为不灵敏损失函数，用于控制回归逼近误差和模型的泛化能力，定义为：
[Li（y）=0，f（x）-y<εf（x）-y-ε，f（x）-y≥ε] （3）
为了将上述约束化问题的求解转变成无约束优化问题的求解，引入拉格朗日乘子[ai]和[a*i]将式（2）的二次优化问题转换成如下对偶问题：
[maxW（a，a*）=i=1nyi（ai-a*i）-εi=1n（ai+a*i）- 12i，j=1nyi（ai-a*i）（aj-a*j）（xi?xj）s.t. i=1nai=i=1na*i，0≤ai≤C，0≤a*i≤C， i=1，2，…，n] （4）
根据泛函原理，满足Mercer条件的函数都可以作为支持向量机的核函数，用核函数来代替上式中的内积计算，此时，回归函数表示为：
[f（x）=i=1n（ai-a*i）K（x，xi）+b] （5）
式中：[K（x，xi）]表示核函数。
2 基于支持向量机的频谱小时空闲度预测模型
GSM系统是当前应用最为广泛的移动通信系统，但是相关研究[10]表明，分配给GSM系统的频谱资源目前并未被充分利用，其下行频点的利用率仅为20%左右。这表明在GSM频段存在认知无线电用户可以进一步利用的大量频谱机会。下文将分析GSM频段的载频使用规律，建立基于支持向量机的预测模型，对GSM载频的小时空闲度进行预测。
2.1 数据分析
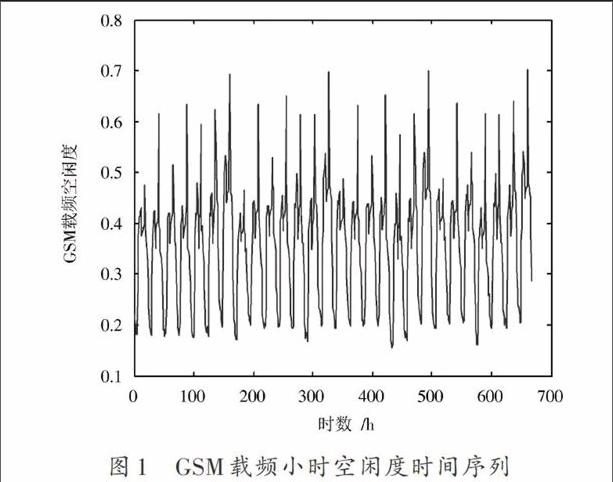
样本的性能对预测模型的学习效果有着极为重要的影响，合适的样本能够为提高预测模型的正确率提供良好的支持。因此，选择样本应尽可能全面地反映研究对象的工作过程和参数特性。以某GSM小区28天的载频小时空闲度时间序列为例（见图1），一方面，由于受到用户习惯、突发事件和地域性等多种因素的影响，载频小时空闲度的变化体现出不确定性，了解未来空闲度的可能变化的一个有效方法，就是利用时间序列本身数据间的关联性，建立与之相拟合的模型。另一方面，正常情况下，GSM载频小时空闲度的短期变化趋势是连续的，而长期变化具有明显的周期性，周期性具体体现在话务量具有日周期性、周周期性、年周期性以及节假日特性。因此，为了提高模型的预测精度，在构建模型时应考虑这一周期性特点。

图1 GSM载频小时空闲度时间序列
2.2 数据重构
根据2.1节的分析，输入向量的选择必须能够体现数据的特征，输入和输出向量之间应具有较强的关联性，预测模型才能实现高精度预测。考虑到空闲度时间序列中，工作日与周末的空闲度数值序列相差较大，呈现出不同的特点。因此，本文首先将训练数据按工作日和周末分解成两个序列，然后考虑到空闲度时间序列的日周期性特点，将数据序列按一天的不同小时时段划分为24个子序列，再对每个时段的子序列分别建立基于支持向量机的预测子模型。对于时间序列预测，需要对预测模型的输入输出数据进行重构。序列的重构数据嵌入维数[m]的确定方法采用计算序列自相关系数的方法。按照公式（6）计算序列的自相关系数，相关度在[0.8 1]之间认为是强相关，应作为输入向量的元素。
[ρx（k）=Rx（k）σx=E[xnxn+k]σx] （6）
具体的数据重构方法如下：
先将时间序列数据分为训练集[Xtrain]和测试集[Xtest：]
[Xtrain=xn，n=1，2，…，T] （7）
[Xtest=xn，n=T+1，T+2，…，N] （8）
然后，按照嵌入维数[m]和星期因子建立输入[xn={xn-1，xn-2，…，xn-m}]与输出[yn=xn]之间的映射关系，从而得到用于模型的训练和测试样本集：
[X=x1x2…xmx2x3…xm+1????xT-mxT-m+1…xT-1xT-m+1xT-m+2…xT????xN-mxN-m+1…xN-1=XtrainXtestY=xm+1xm+2?xTxT+1?xN=YtrainYtest] （9）
2.3 预测流程
采用支持向量机对每个时段构建小时空闲度预测子模型的流程如图2所示。
3 仿真及性能分析
本节通过计算机仿真验证预测模型的性能，并与神经网络模型进行对比分析。
实验数据选自我国中部某城市人口密集地区GSM基站子系统的OMC?R操作维护中心，根据该中心记录的原始运维数据进行统计分析，获取载频小时空闲度时间序列，样本为2009年2月1日至5月30日共129天的小时空闲度数据。前127天数据用于模型训练，其中节假日和周末的小时空闲度时间序列数据一起训练，5月29（工作日）和30日（周末）数据用于测试。
按式（6）分别计算工作日和周末的24个时段子序列的嵌入维数。采用径向基核函数，运用交叉验证算法寻求每个子序列预测模型的惩罚因子[C]和核函数参数的最优值。
图2 载频小时空闲度预测流程图
图3，图4分别是根据上述方法得出的工作日和周末各时段的频谱空闲度预测值。从曲线可以直观地看出，无论是工作日还是周末日，基于支持向量机模型的频谱空闲度预测值与实际值的拟合程度都很高，说明本文所述的建模预测方法能对频谱空闲度进行比较准确的预测。
图3 工作日预测结果
图4 周末预测结果
使用相同的数据并在同样的环境下建立基于BP神经网络的回归模型对频谱小时空闲度进行预测，比较预测结果。BP神经网络采用三层结构，隐含层选择[S]型函数，采用与本文模型相同的输入向量，输出层为1个节点，隐含层为12个节点，训练的目标误差为0.001，最大训练次数为10 000。使用上述方法分别对工作日和节假日各时刻的空闲度进行预测，通过比较说明各方法的优缺点。
两种不同方法在工作日和周末的预测绝对误差曲线如图5和图6所示。从图中曲线可知，相对于传统的三层神经网络预测模型，本文提出的基于支持向量机的预测模型在预测精度上均有了较大改善。总体来看，本文预测模型的绝对百分比预测误差在4%以内，平均绝对百分比误差为2.13%；而神经网络预测方法的绝对百分比误差在5.5%以内，平均绝对百分比误差为4.15%。因此，该方法是有效可行的。
图5 工作日预测误差对比
图6 周末预测误差对比
4 结 语
本文通过分析GSM系统载频小时空闲度特性及预测特点，提出了基于支持向量机回归理论的载频小时空闲度预测模型，在模型设计中考虑到数据的日周期性和节假日特性，以最大程度地挖掘频谱空闲度的变化特征，提高预测精度。
仿真结果表明，本文方法与基于神经网络的预测模型相比，能更好地拟合频谱小时空闲度时间序列的演变规律，预测精度更高。在下一步的研究中，将利用小时空闲度预测结果改进认知网络的路由决策机制，提高认知用户的端到端服务性能。
参考文献
[1] HAYKIN S. Cognitive radio： brain? empowered wireless communications [J]. IEEE Journal of Selected Areas in Communications， 2005， 23 （2）： 201?220.
[2] KARTLAK H. Performance improvement of secondary user transmission in cognitive radio networks [C]// 2012 20th Signal Processing and Communications Applications Conference （SIU）. [S.l.]： [s.n.]， 2012： 1?4.
[3] CACCIAPUOTI A S. Primary?user mobility impact on spectrum sensing in cognitive radio networks [C]// 2011 IEEE 22nd International Symposium on Personal Indoor and Mobile Radio Communications （PIMRC）. [S.l.]： IEEE， 2011： 451?456.
[4] CAGATAY Talay， ALTILAR A T， KHALID D， et al. Impact of mobility prediction on the performance of cognitive radio networks [C]// 2010 Wireless Telecommunications Symposium （WTS）. [S.l.]： [s.n.]， 2010： 1?5.
[5] YARKAN S， ARSLAN H. Binary time series approach to spectrum prediction for cognitive radio [C]// Proceedings of 2007 IEEE 66th Vehicular Technology Conference. [S.l.]： IEEE， 2007： 1563?1567.
[6] 朱江.频谱感知算法及授权用户用频行为研究[D].武汉：华中科技大学，2010.
[7] TUMULURU V K， WANG P， NIYATO D. A neural network based spectrum prediction scheme for cognitive radio [C]// Proceedings of 2010 IEEE International Conference on Communications. [S.l.]： IEEE， 2010： 1?5.
[8] 后茂森，谢显中.基于马氏链的感知无线电信道状态预测及容量估计[J].重庆邮电学院学报：自然科学版，2009（6）：710?716.
[9] VAPNIK V N. The nature of statistical learning theory [M]. New York： Springer， 1995.
[10] 蔡希，罗亚丹.GSM频谱有效使用的研究（上）[J].广东通信技术，2000，20（3）：7?12.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 3:13:16