网站首页  词典首页

请输入您要查询的论文：

　

标题 基于改进半边数据结构的计算机仿真3D建模平台研究
范文 戴艳红+崔健



摘 要： 研究并实现了一个交互式的三维建模系统，该系统以边界表示法表达三维模型为理论基础，同时提出一种改进的半边数据结构来表达三维模型，通过欧拉算子生成各种形体。系统实现了模型切割、实体交并差的布尔运算，以及对实体的体积、表面积的计算。在场景渲染方面，利用OpenGL或者Direct3D的库函数结合系统所采用改进的半边数据结构实现了3D模型的渲染。在仿真模块实现了三维实体的体素化算法，该算法采用正四面体和长方体相结合的八叉树三维空间分割法对实体进行空间分割，实现了对物体重心的计算，最后用该系统实现了一个螺纹铣削加工的仿真实例。
关键词： 三维建模； 半边数据结构； 欧拉操作； 交互式技术
中图分类号： TN911?34； TM417 文献标识码： A 文章编号： 1004?373X（2017）01?0159?04
Abstract： An interactive 3D modeling system is studied and implemented， which takes the boundary representation method to represent the 3D model as the theoretical foundation. An improved half?edge data structure is proposed to represent the 3D model， and various forms are generated by means of Euler operator. The model cutting， Boolean operation of the entity intersection difference， and calculation of the entity volume and superficial area were realized in the system. The 3D model rendering was realized by means of the fusion of OpenGL or Direct3D library function with the improved half?edge structure of the system. The voxelization algorithm of the 3D entity was implemented in the simulation module， by which the octree?based 3D space segmentation method combining the regular tetrahedron with cuboid is used to segment the entity space to calculate the center of gravity of the object. A simulation example of the thread milling was realized with this system.
Keywords： 3D modeling； half?edge data structure； Euler operation； interactive technology
0 引 言
三维建模在计算机仿真领域占有非常重要的位置，是活跃的科学和工业研究领域[1]。本文对计算机仿真三维建模平台设计的各个环节进行了详细的讨论和分析，实现了基于改进的半边数据结构的多面体欧拉操作算子，同时以欧拉操作算子三维实体造型高级操作实现了一个实时、便捷、高性能的面向计算机仿真的三维建模平台。
1 系统平台总体设计
1.1 系统总体结构
本系统从面向对象的模块化设计出发，遵循了高内聚低耦合的原则，系统总体结构图如图1所示。
1.2 控制模块
控制模块是中央枢纽，主要用于维护系统中各个模块间的协同运行，有条不紊地按照一定策略处理每个事件。由于在三维场景中，有大量的事件产生，有些事件可以并发进行，但有些事件是互斥的。因此，需要控制模块统一调度它们，以保证程序能高效、正确地运行[2]。
首先该模块维护一个里面存放需要处理的所有消息的消息队列。在系统运行的过程中，如果需要完成某个事件，要向控制模块提出申请，然后由控制模块生成一个消息放入消息队列等待处理。在这个消息队列中，每一个元素都代表一个事件，它是从系统其他模块发送过来，要求执行某种操作的消息事件，至于这件事情能否得到处理，对于发送消息端来说，不会进行判别。
每个规定的时间片内，控制模块扫描整个消息队列，查看有没有满足触发条件的消息，如果有则建立事件处理列表，按照优先级将需要处理的事件按顺序排好，然后依次执行。
1.3 场景管理模块的设计
场景管理模块是一个核心模块，它负责对系统内部所有对象的管理，包括生成对象、改变对象属性、删除对象等一系列管理操作，同时管理场景内的灯光，场景观察矩阵的设置等[3]。
（1） 对象类的设计
本系统的所有对象都必须接受场景管理系统的管理，因此需要设计一个完整的类层次。本系统所有的类都继承自节点类，这个基类派生出来的所有类组成了以这个基类为根的一个类继承树。
（2） 场景管理
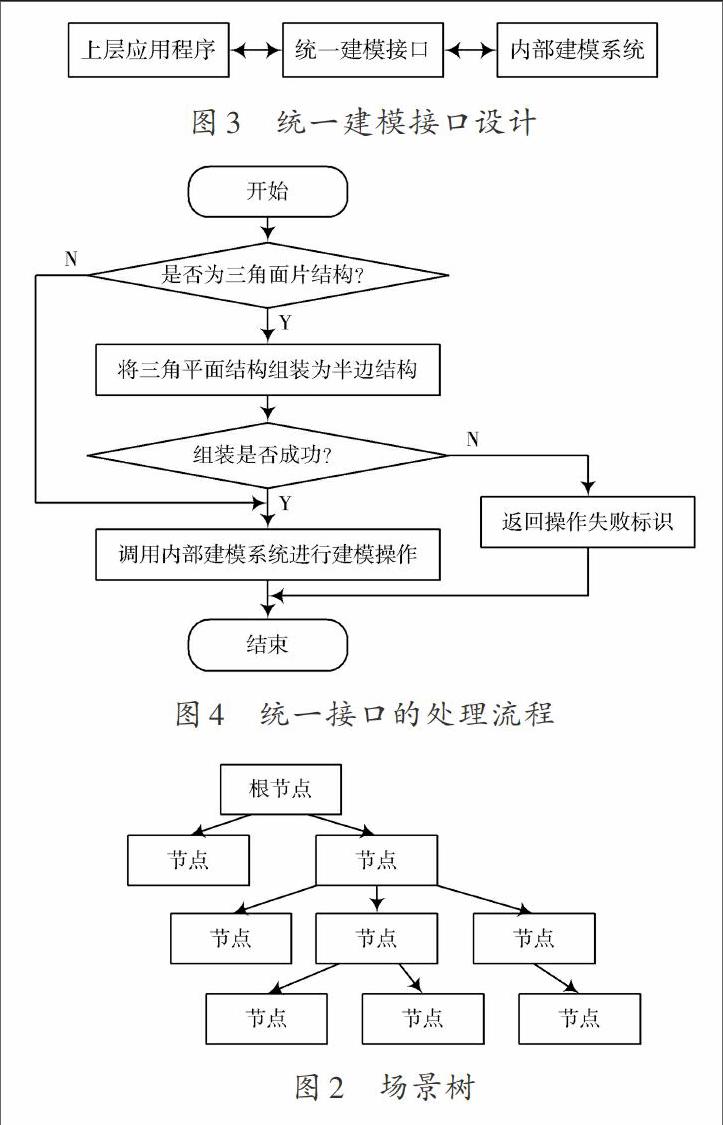
在物体类的继承关系中，所有物体都派生于同一个基类，即节点类，这样便于场景统一管理。在节点类中，不但包含了自身的相关属性，还包括了一个指向孩子节点的指针数组和指向父亲节点的指针。整个场景里的所有物体形成一棵场景树，场景树的根节点就是一个三维场景的根节点，在一个三维场景中只有一个根节点，如图2所示。
1.4 几何造型模块的设计
（1） 本系统采用的三维模型表示方法以及数据结构
在本系统中，设计了一种新的模型数据结构，是一种改进的半边数据结构。本系统采用的几何模型数据结构在半边结构原有的拓扑结构上增加了一个节点类型——三角片节点，这类节点描述面上的一个小三角片，它有1个指向其父面的指针，3个指向顶点节点的指针，1个指向后继三角片节点和前驱三角片节点的指针构成一个小平面的所有三角片的双向链表[4]。
（2） 基于欧拉算子的边界几何造型技术
在本系统中，对于生成的实体是否合法也采用该公式进行检查，以保证所有参与几何造型的形体都符合欧拉不变性原理。
欧拉操作用于对等数据的增、删过程，也就是对实体进行造型过程。这种造型步骤是低层次的、繁琐的，不适用于人机交互，但却是实体造型系统中高层次的几何造型操作（如实体切割、扫掠技术、实体贴合等）的构成基础。
1.5 建模系统统一接口的设计
在本系统中，为了提供二次应用开发的功能，本系统将所有的建模功能、场景对象管理的功能都封装在一个动态链接库内执行，如图3所示。
为了实现对模型数据结构的支持，统一接口的设计中必须包含对数据结构的处理。当使用三角片网格模型时，统一接口模块将对这些三角片网格模型进行半边结构的转换。内部建模系统完成建模操作之后，统一接口模块还必须提供两种数据结构类型的处理结果给用户，让用户根据需要进行选择。统一接口模块的操作流程如图4所示。
通过统一接口标准向外提供功能，可以很好地实现操作的稳定性和安全性，同时也让系统可以很快速地进行二次开发，并且实现平台的移植。
2 三维建模平台关键技术的研究与实现
2.1 基于扫掠算法的基本几何图元的生成实现
在本系统中，利用欧拉操作和扫掠操作以生成若干基本三维实体[5]。
长方体：一次mvfs生成空元体；三次mev算子生成底部矩形的三条连续边；一次mef生成底部的长方形面；以底部的长方形面为基，沿高度方向做一次平移扫掠。
圆柱体（假设圆柱体底面圆的分割条数为n）：一次mvfs生成空元体；次mev生成逼近底部圆的条连续边（未封闭）；一次mef生成封闭的底部圆面；以底部的圆面为基，沿高度方向做一次平移扫掠。
球体：一次mvfs生成空元体；次mev生成逼近半圆弧的条连续边；以连续边两个端点的连线为旋转轴，以连续边为基做一次以线为基的旋转扫掠。
圆锥体：一次mvfs生成空元体；一次mev生成一条边，这条边将作为圆锥体侧面的母线；以上一步生成的边为基，这条边的一个端点在圆锥体的顶点上，另一端在底部的圆上，以圆锥顶点和底部圆心的连线为转轴，做一次旋转扫描。
圆环体：一次mvfs生成空元体；次mev生成一个未封闭的平面区域；一次mef生成封闭的平面区域；以该平面区域为基，以指定的转轴做一次旋转扫描。
2.2 特征造型技术的研究与实现
孔洞的特征即在实体表面，朝着面法向量的反方向“挖”出一个凹陷的部分。一般的孔洞特征有方形孔洞，圆形孔洞等。
凸台的特征即在实体表面，朝着面法向量的正方向“拔”出一个凸起的部分來。一般的凸台特征有方形凸台、圆形凸台等。
倒角造型是对实体中过渡剧烈的边进行钝化，使实体表面更为平滑过渡。
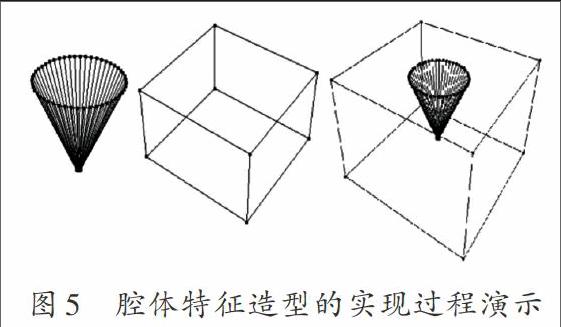
腔体造型在生成带有内腔特征的几何形体时，可以非常方便地实现。本文以腔体为例具体介绍其设计与实现。
通过一个简单的腔体模型来说明腔体构造（见图5）的生成算法，以在六面体内部产生一个圆锥体空腔。具体操作步骤如下：
（1） 首先选择主模型和空腔模型，即选择六面体为主模型，圆锥体为空腔模型；
（2） 选择主模型开孔面，即六面体中的顶面；
（3） 选择空腔模型的开孔面，即圆锥体的底面；
（4） 对空腔模型世界位置的位置矩阵进行变换，使它的下底面能够和正方体顶面重合；
（5） 对空腔模型所有面的法向量置反；
（6） 合并主模型和空腔模型，即合并两个实体的半边数据结构，形成一个具有两个壳体的数据结构；
（7） 连接这两个壳。在两个开孔面上，以六面体模型的顶面为主面，以圆锥体的底面为辅面，使用kfmrh算子将圆锥体底面的外环变成六面体顶面的内环边界[6]，便形成了带有圆锥腔体特征的六面体模型。
2.3 实体分析计算
（1） 半边结构实体的欧拉不变性检查和结构合法性检查计算
半边结构实体的欧拉不变形检查是根据欧拉公式和来判断一个实体是否符合欧拉原理。
在半边数据结构中有大量的指针，这些指针在欧拉操作中要保证它们是合法的，例如一条边必须拥有两个半边节点的指针he1和he2，否则就是一个不合法的数据结构，父子关系的指针也必须保证是正确的。
在进行几何造型编辑操作之前，首先检查半边结构是否合法，是否符合欧拉公式，如果不合法，则不进行操作，以保证程序能正确执行。
（2） 实体表面积计算
求多面体的表面积就是求全部小平面的面积之和。因为一个平面可能是复连通的，所以计算一个小平面的面积就归结为计算若干个平面单环的面积，用外环的面积减去全部内环的面积。
由矢量代数可知，两矢量与的矢量积的模为sin（angle），angle为与之间的夹角。它恰好等于以和为边的平行四边形的面积。
因此可以采用如下方法计算多边形的面积：将环的第一个顶点作为参考点，环所围的面积area为多边形法向量normal和矢量的点积之和：，其中为边对多边形面积的作用。等于矢量和的叉积：由于normal与同向，所以。
2.4 实体的显示与场景渲染优化
（1） 基于半边结构的小平面三角剖分实现
本系统采用多边形的梯形三角剖分法，算法如下[7]：
步骤1：将多边形的顶点按照某一方向进行排序。
步骤2：依次从顶点作扫描线，同时记录交点，将多边形划分成梯形。
步骤3：将梯形划分成三角形。
（2） 场景渲染优化
本系统实现了基于视锥体原理的场景渲染优化。判别物体是否进入视锥体的空间采用将实体包围盒与场景视锥体进行求交计算，如果相交了，则认为这个实体进入了视锥体空间。这个方法可以简单快速地实现场景渲染的优化。
2.5 三角片网格模型向半边结构的转化研究与实现
三角片网格模型半边数据结构进行转换的算法如下[8]：
步骤1：构建一个半边结构的三维实体，将三角片网格模型中所有的顶点加入该半边结构中。此时面片信息为空，边节点信息也为空。
步骤2：将所有三角片看成是一个独立的小平面，加入半边结构。此时面与面之间不包含边节点信息。
步骤3：构建边节点信息。构建边节点的过程是遍历上一步中所有的小平面，假如在一个小平面中存在一个半边，那么搜索所有的小平面，查找到一个的半边，构建一个边节点，同时将半边和半边作为这个边节点的两个半边。依次构建出所有的边节点。
步骤4：步骤3完成时，此时半边结构已经形成，但是此时不是一个合理的半边结构，因为还有大量共面相连的三角片存在。在这一步中，通过kef算子将共面相连的三角片连接，形成小平面。
3 平台试验结果展示
图6～图9分别展示了扫掠算法的实现演示，包括平移扫掠算法、以面为基旋转扫掠算法、以线为基旋转扫掠算法以及轨道扫掠算法。
从实验结果可以看出，当空间分割次数逐渐增加时，体素化的结果逐渐接近原边界模型，体积误差越来越小，体素模型逐渐接近原表面模型，但是计算时间也将增加。
4 结 论
本文设计了一个基于欧拉算子的几何造型平台。在欧拉算子的基础上，研究了基于欧拉算子的扫掠算法和几何造型算法。为了提高建模的效率，还研究了基于特征的造型算法，实现将零维、一维和二维形体合理地纳入到三维造型系统中，而且通过半边结构将它们正确地表达出来。
同时，针对半边结构特点的层次化存储方案，将几何模型的数据合理地保存与读取。实现了基于半边结构模型的体素化算法，并且分析传统长方体八叉树空间分割算法異常点的情况，结合正四面体八叉树空间分割算法的稳定性，提出了将长方体和正四面体相结合的实体空间体素化，通过本系统验证表明，这是一种有效的体素化方案，可以尽可能地逼近原边界模型。
参考文献
[1] EDELSBRUNNER H. Key problems and key methods in computational geometry [M]. Berlin： Springer， 2005： 1?13.
[2] BARNHILL R E， BOEHM W. Surfaces in computer aided geometric design [M]. New York： North?Holland Publishing Co.， 1995： 1?17.
[3] 刘晓平，田景成.基于模板的工程CAD设计方法研究[J].计算机辅助设计与图形学学报，1999（4）：296?299.
[4] 唐良红，孙立镌，宋双柱.CAID系统的数据结构[J].哈尔滨理工大学学报，1998，3（3）：1?5.
[5] 唐荣锡.三维几何造型[J].浙江大学学报，1982（4）：22?25.
[6] MANTYLA M. An introduction to solid modeling [M]. New York： Computer Science Press， 2003： 27?66.
[7] 李新友，唐泽圣，孙家广.正则几何形体及正则集合运算[J].计算机学报，1989（3）：162?171.
[8] CHAZELLE B， EDELSBRUNNER H. An optimal algorithm for intersecting line segments in the plane [J]. Journal of ACM， 1992， 39（1）： 1?54. 技术文
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 23:41:30