《概率论在日常生活中的若干运用研究》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

概率论在日常生活中的若干运用研究

范文

布合力且木?阿不都热合木

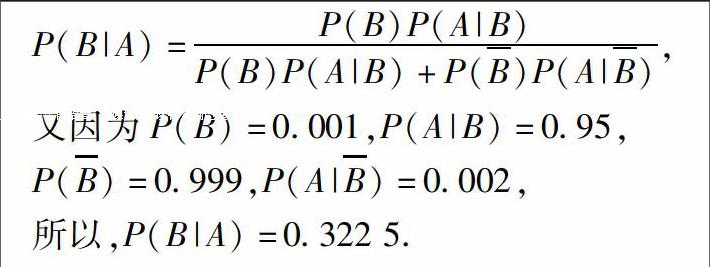
【摘要】概率论是数学学科中一门研究概率问题的分支.概率论在研究和预测数据方面，有着其很强的逻辑性，在日常生活中，很多事情都运用到概率论知识.在本文的研究过程中，选取了几个方面的案例进行了深入探讨，希望可以对概率论的应用起到一定的有益思考.

【关键词】概率论；投资决策；次品率；保险精算；产品质量；随机问题

概率论是研究随机现象中统计规律的专业性学科，在日常生活中，往往有很多事件的发生都是随机的，这就为概率论的应用提供了良好的素材.虽然随机的事件发生具有一定的偶然性，但是对大量的随机事件进行统计分析之后，就会发现大量的随机事件有着一定的规律性.例如，购买保险的人们，在一年之后出现事故的概率；连续向上抛硬币，正反面朝上的次数比率；投资项目的成功率等，都具有一定的内在规律.以下是本文选取的几个概率论运用的日常生活案例.

一、概率论在疾病确诊率方面的运用

通过对大量以往诊断病例数据的分析，某医院确定出对某疾病能够成功诊断的概率是0.95，没有疾病而被误诊的概率是0.002，如果在医院所在区域内，该疾病的患病比例是0.001，现在在该地区随机抽取一人，对其进行疾病诊断，诊断结果显示该患者患有该疾病，请问该人确实患有该病的概率.

解析为了在数学概率计算时更加简单，我们设B=该人患有该病，A=该人诊断患有该病，则所求概率为：P（B|A），依据貝叶斯公式得

P（B|A）=P（B）P（A|B）1P（B）P（A|B）+P（B）P（A|B），

又因为P（B）=0.001，P（A|B）=0.95，

P（B）=0.999，P（A|B）=0.002，

所以，P（B|A）=0.322 5.

这个结果说明，在某一人诊断后患有该疾病的情况下，其真实患有该疾病的概率依然不高，接近三分之一.这个概率案例，说明了在医院进行诊断，很多情况下，诊断结果都是一个概率性的参考.

二、概率论在人寿保险方面的运用

有2 500人参加某保险公司的人寿保险，据以前统计资料，一年内每个人死亡的概率为0.000 1，每个参加保险的人1年付给保险公司120元保险费，而在死亡时其家属从保险公司获得20 000元赔偿费，求下列事件的概率：

A=保险公司亏本，B=保险公司一年获利不少于十万元.

分析假设这2 500人当中有k个人死亡，则保险公司亏本当且仅当20 000k>2 500×120，即k>15.又由二项分布公式知，1年中有k个人死亡的概率为

Ck2 500（0.0 001）k（1-0.0 001）2 500-k，

k=0，1，2，…，2 500.

所以，保险公司亏本是几乎不可能的.

因为保险公司一年获利不少于十万元的概率等价于2 500×120-20 000k≥105，即k≤10.

由此可见，保险公司1年获利十万元几乎是必然的.

三、概率论在产品质量责任追究方面的运用

某工厂4个车间生产同一种产品，其产量分别占总产量的0.15，0.2，0.3，0.35，各车间的次品率分别为0.05，004，0.03，0.02，有一用户买了该厂1件产品，经检查是次品，用户按规定进行索赔.厂长要追究生产车间的责任，但是该产品是哪个车间生产的标志已经脱落，怎么追究生产车间的责任？

分析由于不知道该产品是哪个车间生产的，因此，每个车间都要负责任，各车间所负责任的大小应该正比于该产品是各车间生产的概率的大小.

设Aj=该产品是j车间生产的，j=1，2，3，4；B=从该厂产品中任取一件恰好取到次品.

则第j个车间所负责任大小（比例）为条件概率：

P（Aj|B），j=1，2，3，4.

由贝叶斯公式得

P（Aj|B）=P（Aj）P（B|Aj）1∑41i=1P（Ai）P（B|Ai），j=1，2，3，4.

又因为P（A1）=0.15，P（A2）=0.2，P（A3）=0.3，

P（A4）=0.35，P（B|A1）=0.05，P（B|A2）=0.04，

P（B|A3）=0.03，P（B|A4）=0.02，

从而P（A1|B）=0.15×0.0510.0 315=0.238，

P（A2|B）=0.2×0.0410.0 315=0.254，

P（A3|B）=0.3×0.0310.0 315=0.286，

P（A4|B）=0.35×0.0210.0 315=0.222.

即第1，2，3，4车间所负责任比例为0.238，0.254，0286，0.222.

而车间的管理者，通过对上述承担责任概率的分析，就会使得奖惩机制变得更加科学合理，也能够促进车间的质量管理工作水平不断提高.

四、概率论在项目投资预测中的运用

（一）投资风险预测

在投资之前，要对投资风险进行预测.投资风险预测，在概率论上，属于随机决策的一种.在预测时，需要对投资项目面临的主要风险事件的概率进行自然状态下的科学分析，然后对不同的风险事件发生的概率进行对比，确定选择风险相对较小的投资决策方案.这其中相关风险事件的预测分析，需要用到概率论知识.例如，一些可能发生的风险事件的概率、正态分布、泊松分布等.

（二）投资成本预测

投资成本不是一成不变的，在实际投资进行阶段，可能会面临一些其他变化情况，从而导致投资的成本发生变化.因此，在做成本预算时，需要对在投资过程中，可能发生的影响成本变化的事件概率进行预测分析，并通过概率计算公式，计算出这些未知因素对投资成本可能发生的影响系数.例如，假定初始投资预算是100万，在后续投资过程中，不发生任何影响投资成本变化的事件，则初始投资成本不变.不过由于受到一些因素的影响，CPI走高、工人工资上升、原材料物价上涨，这些因素组合在一起，在概率上会有95%可能使得投资成本提高10%，则在这种情况下，就可以通过概率计算出投资成本的变化范围，从而提前做好资金追加的准备，保证在上述事件发生时，能够从容应对.

（三）资金回收率预测

概率论在预测资金回收方面，能通过构建预测体系，将影响资金回收的各种事件的状态划分为定型状态和不定型状态两类.对应的投资项目下，能够及时回收的资金就是定型状态，而不能及时回收的资金就是不定型状态.而上述的不定型状态和定型状态的事件之间，可以在一定的条件下相互转化，结合概率论的相关知识，二者能够转化成概率矩阵，在概率矩阵计算时，能够通过对相关系数的确定，计算出最终能够有效回收的资金.

五、结束语

概率论的内容丰富而复杂，不仅在很多专业学科的研究中发挥着很大的作用，而且概率论本身的生活应用性也很强.例如，日常生活中买彩票、玩扑克牌等小游戏，都涉及一些概率论的知识，这些概率论的知识虽然比较浅显，但是其核心思想内涵，依然是随机事件发生的概率研究问题.在本文的研究过程中，通过对一些概率论案例的分析研究，说明了概率论在解决实际生活问题上的优势和可行性，希望可以对概率论的普及发展，起到一定积极作用.

【参考文献】

[1]缪彬.基于软集合理论的不确定性多属性决策方法研究[D].昆明：昆明理工大学，2014.

[2]姜颖，王晓锋.以概率论的视角理性看待社会热点[J].沈阳师范大学学报（自然科学版），2012（1）：27-31.

[3]陈海杰，沙荣方，刘明华.应用案例分析提高概率论与数理统计教学效果[J].东北农业大学学报（社会科学版），2012（1）：98-100.

[4]刘国祥，张晓丽，杨永霞，刘冬，李玉毛，由向平.应用型人才培养模式下概率论与数理统计课程改革探索与实践[J].赤峰学院学报（自然科学版），2014（23）：1-5.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。