欧阳文 陈丹


摘? 要:颗粒粒径在制药、食品加工等领域中都是一个重要的参数,通过测量、控制颗粒粒径可以有效地提高生产力、产品质量和过程效率。该文研发设计了一种衍射式粒径分布测量装置,并根据积分变换反演方法,利用小角度内的衍射光信息,通过基于闭环控制原理的粒径分布重建方法进行粒径分布测量计算。解决了积分变换反演方法在Fraunhofer衍射式粒径分布测量的应用中,克服了原积分变换反演方法重建精度低、分辨能力差的缺点,而且结构简单,容易实施。
关键词:闭环控制;粒径分布;测量方法
中图分类号:TP391? ? ? ? 文献标志码:A
0 引言
颗粒粒径在火力发电厂、制药、化工和食品加工等领域[1]中都是一个重要的参数,在这些领域中,通过测量、控制颗粒粒径可以有效地提高生产力、产品质量和过程效率[2-3]。因此,人们在过去的数十年间研究并发展出多种测量方法,比如显微镜、筛分、沉淀、光散射、气体吸附等。其中,光散射法以其快速、非侵入、宽动态范围和较高的准确性等特点,在实际应用中占主要地位。光散射法粒径分布测量的基本原理是由激光器产生一束入射光,入射光接触样品池内的待测颗粒系并发生散射,散射光被位于样品池另一端的光电探测器阵列接收。根据测得的散射光的光强分布情况,通过求解逆散射问题,以此来获得待测颗粒系的粒径分布情况[4]。
在一些工业场合中,颗粒粒径远大于入射光波长,就可以忽略前向散射光中的散射和反射,只考虑颗粒带来的衍射效应,将Mie散射理论简化为Fraunhofer衍射,以此来近似刻画小角度内的前向散射光分布[5]。当入射光为可见光时,这种近似对于粒径大于5 wn的颗粒是完全适用的。根据衍射光强分布来重建粒径分布,属于逆问题求解的范畴,求解该逆问题时往往伴随着求解病态方程组、数值解不稳定等问题,因此,如何根据衍射光强分布准确地重建粒径分布是粒径分布测量的关键[6]。
该文以衍射式粒径分布测量装置、积分变换反演方法为基础,利用小角度内的衍射光信息,通过基于闭环控制原理的粒径分布重建方法进行粒径分布测量。克服了原积分变换反演方法重建精度低、分辨能力差的缺点,而且结构简单,容易实施。
1 技术内容
该文主要解决积分变换反演方法在Fraunhofer衍射式粒径分布测量的应用中,由于仅能获得有限小角度内的衍射光信息,而导致对窄分布粒径颗粒分辨能力差、重建精度低的问题。
基于闭环控制原理的粒径分布测量方法,以Fraunhofer衍射理论为基础,通过环形光电探测器获得衍射光的光能分布,并将一般的积分反演方法扩展为基于闭环控制理论的迭代法,以此来完成粒径分布的重建。
该文所采用的测量装置结构元件包括可见光激光器、扩束镜、光阑、样品池、傅里叶透镜、环形光电探测器、数据采集卡和上位机等。
2 方法步骤
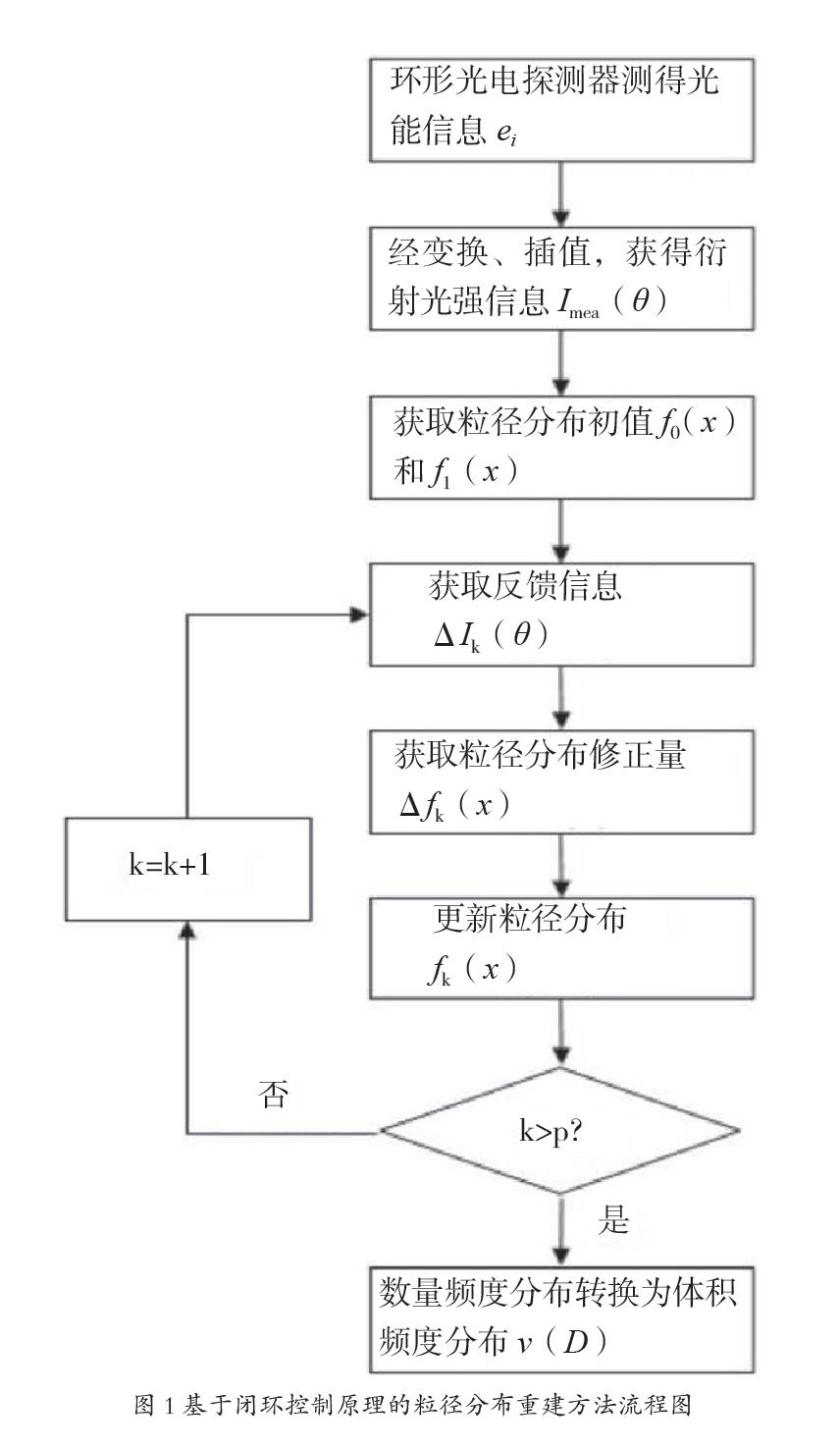
方法步骤流程图如图1所示。
步骤一,可见光激光器发出波长为λ= 635 nm的激光,经扩束镜、光阑后形成一束光强为I0的平行单色光,该射光与样品池内的待测颗粒悬浊液接触并发生散射,在傅里叶透镜的后焦平面上形成衍射图样,其中,令I0=1。
步骤二,由位于傅里叶透镜后焦平面的、环数为m=35的环形光电探测器测得光能信号ei并根据公式⑴将光能信号ei变换为衍射光强分布Imea(θi)。
(1)
式中:ei是环形光电探测器中第i环的测量值,i = 1,2,…,m,i是第i环对应的衍射角θ,θ0=0,F是透镜焦距。然后令θmax=θm,并通过插值获得区间内连续的衍射光强分布曲线Imea(θ)。
步骤三,以fk(x)表示粒径数量频度分布第k次重建的结果,获取粒径分布的初值f0(x)以及f1(x),令f0(x)=1/(b-a),并利用公式(2)获得f1(x)。
(2)
式中:θ是衍射角,是透镜焦距;光阑后形成一束光强为,θmax衍射角最大值,dφ是指角度微分;x=nD/λ是颗粒的光学尺寸参数,D是颗粒直径,,J2是二阶第一类 Bessel函数,β是预设的负实数;
步骤四,在获得fk-2(x)和fk-1(x)的基础上,利用公式(3)依次计算反馈信息Iinv,k(θ)、反演误差ΔIk(0)以及粒径分布的修正量Δfk(x),从而更新重建的粒径分布fk(x)。
(3)
式中:J1是一阶第一类Bessel函数;λ为波长;θ为衍射角;F 是透镜焦距;x=nD/λ是颗粒的光学尺寸参数。
步骤五,判断重建次数k是否大于预设最大迭代次数p,如果是,则执行步骤六,如果否,则令k=k+1并返回步骤四。
步骤六,将重建的颗粒粒径数目频度分布结果fp(x)转换为最常用的颗粒体积频度分布v(D),并作图显示,如图2所示。
(4)
式中:D是颗粒直径。
3 结论
该文如果是以Fraunhofer衍射式粒径分布测量装置为基础,将闭环控制原理引入粒径分布测量中,以反演误差为控制对象,将原积分变换反演方法扩展为迭代形式的方法,既利用了Fraunhofer衍射式粒径分布测量装置原理和结构简单的优点,又抑制了测得衍射光信息有限对粒径分布测量的不利影响,提高了在实际应用中对窄分布粒径颗粒的分辨能力和重建精度。
参考文献
[1]岳珍,冯珂裕,张娜.阿考替胺原料药粒径筛选与阿考替胺片体外溶出行为一致性评价[J].中国新药与临床杂志,2015(11):879-883.
[2]章维, 苏明旭, 蔡小舒.基于超声衰减谱和相速度的颗粒粒径测量[J].化工学报,2014, 6(3): 898-904.
[3]李红红.航空发动机二维模型燃烧室中碳黑颗粒生成数值模拟[D].南京:南京航空航天大学,2008.
[4]张群杰.航空发动机燃烧室中辐射换热的数值研究[D].沈阳: 沈阳航空航天大学,2012.
[5]Riefler N,Wriedt T. In tercomparison of Inversion Algorithms for Particle-Sizing Using Mie Scattering[J].Particle&Particle Systems Characterization,2008,25(3): 216-230 .
[6]王雪艷,刘缠牢.独立模式反演算法在激光粒度测试中的应用研究[J].激光技术,2011(3):352-355,387.
- 民营企业现金流管理探析
- 企业财务共享服务中心的建设与研究
- 中小民营企业财务内部控制的建立与完善探讨
- 外资企业资金管理存在的问题及对策探析
- 基于生命周期的企业财务战略选择
- 石油企业财务成本精细管理与控制探讨
- 企业财务内控管理制度的建立与完善研究
- 浅谈汽车行业产品生命周期中的财务工作
- 从财务角度看汽车4S店内部控制环节:存在的问题与改进的措施
- 浅析电力企业资金管理存在的问题及对策
- 公允价值模式在投资性房地产中的应用分析
- 数字出版业务的会计核算初探
- 事业单位实行绩效工资存在的问题及对策
- 去产能背景下煤炭企业人力资源风险探究
- 基于BSC的高新技术企业绩效考核研究
- 海洋渔业船员权益的国际法规制
- 建筑施工企业建造合同法会计核算中的问题
- 医院经济合同履约管理内部控制研究
- PPP项目中融资面临的风险及对策
- 国有金融企业内部控制存在的问题与改进对策
- 金融投资公司资金管理存在的问题及对策探析
- 浅析行政事业单位财政项目支出绩效评价
- 农田循环生产技术农户采纳意愿影响因素实证分析
- 基于随机森林融合因子分析的资产收益模型研究
- 浅谈“个人本位”原则对西方思想文化的影响
- preresorting
- preresorts
- prerespectabilities
- prerespectability
- prerespectable
- prerespiration
- prerespirations
- prerespire
- prerespired
- prerespires
- prerespiring
- preresponsibilities
- preresponsibility
- preresponsible
- pre-restoration
- prerestrain
- prerestrained
- prerestraining
- prerestrains
- prerestraint
- prerestraints
- prerestrict
- prerestricted
- prerestricting
- prerestriction
- 馈致
- 馈荐
- 馈诒
- 馈贫之粮
- 馈贶
- 馈贻
- 馈赂
- 馈赆
- 馈赐的食物
- 馈赠
- 馈赠之物
- 馈赠奉献
- 馈赠慰劳
- 馈赠慰问
- 馈赠死者的衣被
- 馈赠用的礼物
- 馈赠的牲畜
- 馈赠的钱财物品
- 馈赠礼物
- 馈赠类
- 馈赠联
- 馈赠财礼
- 馈赠,酬报
- 馈走
- 馈转