《基于区块链的产业供应链金融平台设计与实现》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

基于区块链的产业供应链金融平台设计与实现

范文

王炜

摘? 要：随着p2p平台被全面封杀，供应链金融平台主要转向产业供应链的上下游企业，该平台以服装产业链为试点，以时装周展会为切入点，对设计师、服装厂、买手店、批发商等服装产业链的上下游企业进行整合，以交易订单为风控基础，利用区块链智能合约技术保障交易安全，探索产业供应链金融平台的应用前景。

关键词：区块链;供应链金融;风险控制;智能合约;人工智能

中图分类号： TP311? ? ? 文献标志码：A

1 项目背景

服装产业供应链金融平台的运作以上海纺织集团为依托，以每年的上海时装周的服装贸易背景为前提，运用基于供应链贸易融资的方式，配合智能风控监管等手段，通过供应链全环节的资金流或者物流权，为上下游企业提供授信、清算、资金信贷等综合性金融产品及服务。供应链金融平台实现“物流”“资金流”“信息流”“商流”的四流合一，可以促进整个“链条”的运转，给服装产业链的中小企业赢得了更多的商机。

该项目尝试构建一个以服装产业链订单流为基础的金融平台，采用人工智能技术审核订单的真实性，集中货仓保证物流的稳定性，智能风控保证上下游的企业资金的安全性。探索以订单为抓手，以金融相关产品为驱动，以智能合约体系为保障，利用人工智能进行风险控制的平台运营管理模式。

该平台以上海纺织集团每年的时装周展会为发端，对全球各地顶级设计师的服装作品，采用设计版权引进的方式落地国内的服装企业进行生产，利用线上线下的展会系统全国招商各地的买手店，以上纺集团作为信用担保，整合上海银行、通联支付，形成完整的资金渠道，构建上下游企业的资金信贷产业链。

2 系统需求分析

该系统作为服装产业的供应链平台，从服装展会系统入手，以订单中心为核心，采用数据中台的模式对接服装供应链上下游企业的信息化系统，形成完整的产业订单流转与交换平台。

为保证订单系统的安全性，利用区块链的智能合约功能保障全流程订单全程的安全。同时利用订单中心的交易数据，结合企业征信信息、司法案例信息等，利用人工智能技术实现企业的智能风控体系。

同时为保证可以快速、安全地实现平台需求，采用自行研发的快速开发平台实现[1]。

2.1 服装展会系统

服装展会系统依托上海纺织集团的每年春秋两季举办的上海时装周，采用线上线下展示结合，包含展会管理、设计师管理、服装商城等基础功能，通过微信小程序方便展示与传播。

展会管理是面向服装展会主理人的功能模块，由服装展会主理人发布展会信息，对设计师和品牌进行招商，管理展会场地，并提供物联网接口，其可以与展会闸机厂家对接，提供扫码过闸机的功能。

设计师管理主要面向全球的设计师入驻和品牌、作品发布管理，提供2D照片和3D人模的展示方式，通过AutoCAD的设计图纸智能转换成3D的人体模特，提供可扩展的服装面料库，根据不同服装面料的质感展示不同服装面料的效果。同时可以通过参数调整，动态调整3D人模的体型，展示不同人群的穿着效果，真正实现一套设计百样风格千人千面。

服装商城功能类似目前标准的电商平台，其核心是通过智能分析平台向设计师发布同类竞品的市场价格，给买手进行参考和比对，从款式、品牌、销量等多个维度进行全方位的分析。

2.2 数据中台系统

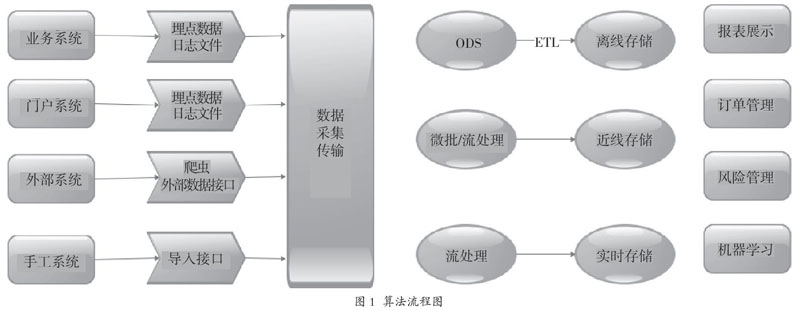
为快速构建系统接口并完善系统功能，该系统的核心功能是构建一个可以快速配置化开发接口和系统功能的数据中台。首先，快速接口配置系统采用类似Visio的流程图界面，主要分成系统接口类模块、ETL类模块、数据算法模块等封装流程功能模块如图1所示。

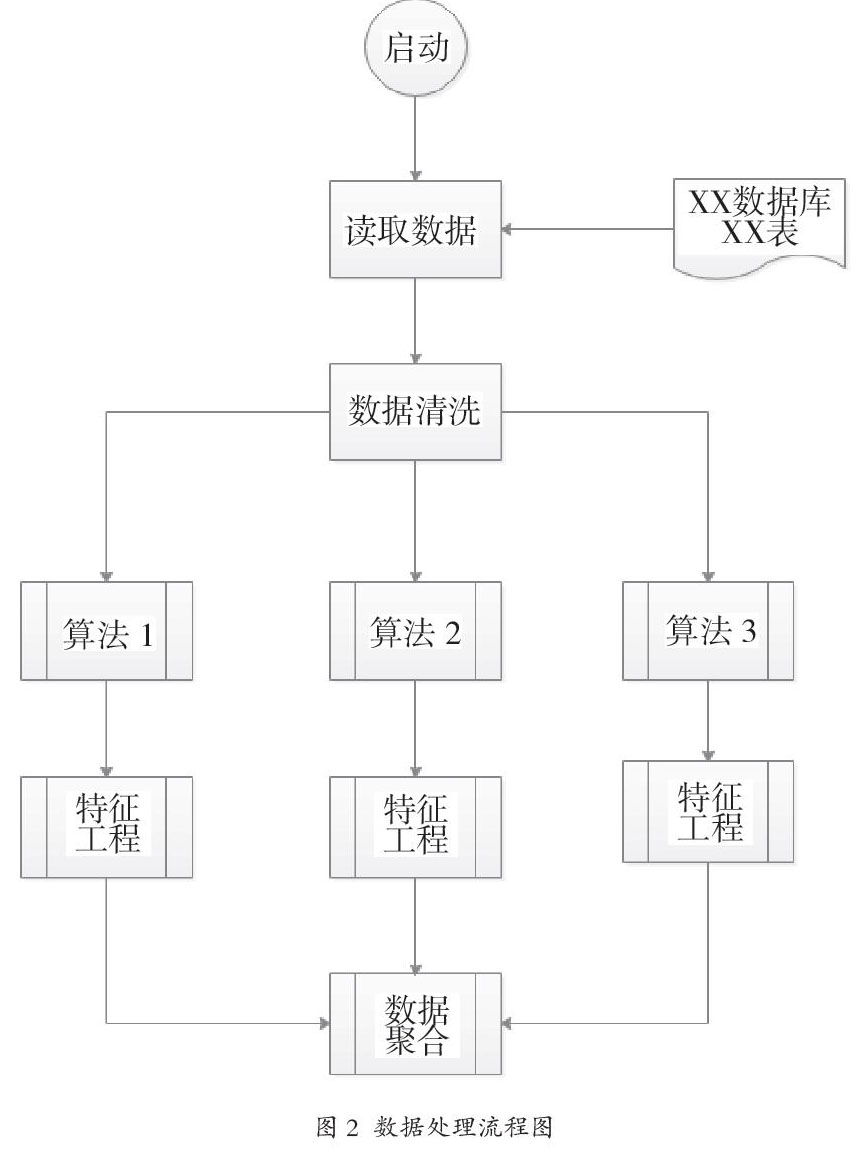
采用如图2的流程图模式对数据处理的流程进行自定义。

2.3 智能风控系统

智能风控系统通过订单中心、通联支付获取企业的征信信息、通过爬虫等技术获取企业税务、法律等相关风险信息。通过对企业订单的资金方、上下游企业、金额等信息进行综合，采用人工智能算法，对可能存在洗钱、欺诈、刷单等行为进行机器识别，并生成告警，提醒运营单位进行审核[2]。

3 技术架構

3.1 智能合约

区块链是一个分布式数据库，记录着区块链网络中曾发生的所有交易，该数据库在网络参与者之间进行复制和共享。区块链的主要特征是其允许不受信任的参与者以安全的方式在彼此之间进行通信并发送交易，不需要受信任的第三方参与。区块链是一个有序的区块列表，每个区块都由其加密哈希标识。每个区块都引用其之前的区块，从而形成区块链。每个区块由一组交易组成。一旦创建了一个区块并将其附加到区块链中，该区块中的交易就无法更改或还原，这是为了确保交易的完整性并防止双花问题。区块链技术的一个吸引人的特征是智能合约。智能合约是在区块链之上运行的可执行代码，可在不受信任的第三方参与的情况下执行不受信任的各方之间的协议。

当前系统中各方之间的交易通常以中心化的形式进行，这需要受信任的第三方（如银行的参与）。但是，这可能导致安全问题（如：单点故障）和高昂的交易费用。区块链技术的出现通过允许不受信任的实体以分布式方式彼此交互不需要受信任的第三方参与，解决了这些问题。区块链是一个记录了网络中曾发生的所有交易的分布式数据库。区块链最初是针对比特币（点对点数字支付系统）引入的，但后来演变为用于开发各种去中心化应用程序。可以部署在区块链之上的有吸引力的应用程序就是智能合约[3]。

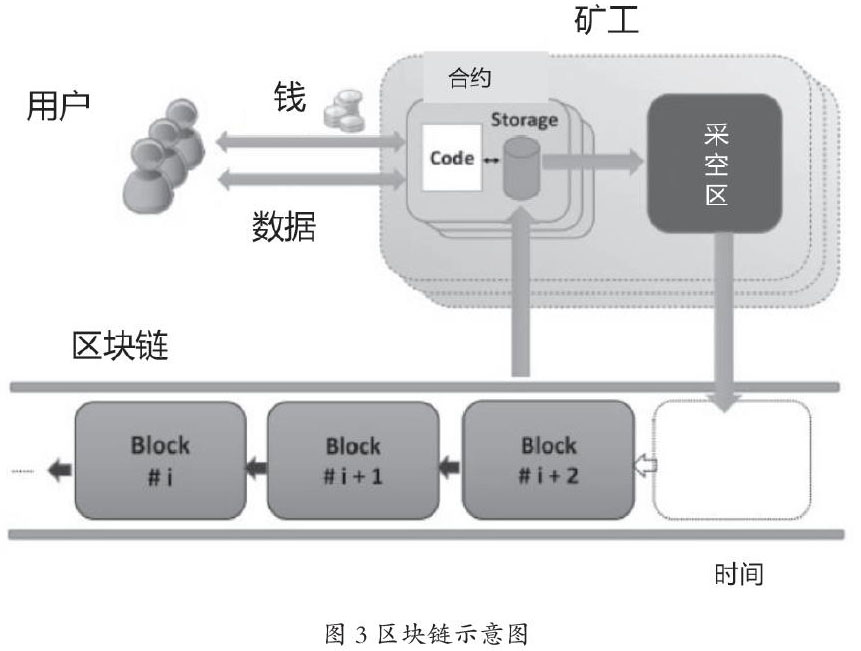
智能合约是在区块链上运行的，用于执行不受信任方之间的协议条款的可执行代码，可以将其视为一种系统，一旦满足预定义的规则，即可将数字资产释放给所有或部分参与方。与传统合约相比，智能合约不依赖可信赖的第三方进行操作，交易费用低。区块链组成如图3所示。

3.2 风控算法

该文主要分享基于模块度的louvain和基于信息熵infomap这2类算法。

3.2.1 基于模块度的louvain

Louvain算法是一种基于图数据的社区发现算法。原始论文为《Fast unfolding of communities in large networks》。

算法的优化目标为最大化整个数据的模块度，模块度的计算如下：

式中：m为图中边的总数量。

Aij代表节点i，j间连接的权重。

即与节点i相连的所有边的权重之和。

CiCj表示节点i， j的commnity index。

函数δ（Ci×Cj）表示节点i，j是否在同一个community中（相同时取1，否则取0）。

有一点要搞清楚，模块度的概念不是Louvain算法发明的，而Louvain算法只是一种优化关系图模块度目标的一种实现而已。

Louvain算法的两步迭代设计：

最开始，将每个原始节点都看成一个独立的社区，社区内的连边权重为0。

算法扫描数据中的所有节点，针对每个节点遍历该节点的所有邻居节点，衡量把该节点加入其邻居节点所在的社区所带来的模块度的收益。并选择对应最大收益的邻居节点，加入其所在的社区。这一过程化重复进行指导每一个节点的社区归属都不在发生变化。

对步骤1中形成的社区进行折叠，把每个社区折叠成一个单点，分别计算这些新生成的“社区点”之间的连边权重，以及社区内的所有点之间的连边权重之和。用于下一轮的步骤1。

该算法的最大优势就是速度很快，步骤1的每次迭代的时间复杂度为O（N），N为输入数据中的边的数量。步骤2 的时间复杂度为O（M + N）， M为本轮迭代中点的个数。

3.2.2 基于信息熵infomap

Infomap 设计之初想解决的问题如下：如果在一张图上做随机游走（不限步数的游走），如何用最短的编码来描述随机游走产生的路径？例如，图4中展示了一段随机游走产生的路径，那怎么描述它先访问了哪个节点，后访问了哪个节点呢？

Infomap 的双层编码方式把群组识别（社区发现）同信息编码联系到了一起。一个好的群组划分可以带来更短的编码。所以，如果能量化编码长度，找到使得长度最短的群组划分，那就找到了一个好的群组划分。

那如何量化编码的长度呢？假设现在有一种群组划分方式 M 将节点划分为 m 个群组，则描述随机游走的平均每步编码长度（average number of bits per step）可以用下面这个公式来度量：

在上面的公式里用到的最重要的概念是信息熵 H（X）。熵在一般的理解里是用來描述“系统混乱程度”的，当一个随机变量为均匀分布的时候，它的状态最不确定，系统最混乱不可预测，这个时候熵最大。

上面的公式里，有4个变量，其含义如下。

假设现在有一种群组划分方式M将节点划分为m个群组。

H（Pi）：编码群组 i 中所有节点所需的平均字节长度（注意：跳出编码也作为一个虚拟节点放在了各自群组内一起编码）。

简单的理解上面这个公式：平均每步编码长度 L（M）是2个部分的加权和，一个是编码群组名字所需的平均字节长度，一个是编码每个群组中的节点所需的平均字节长度，权值是各自的占比。

如果要计算上述4个变量的值，我们只需要知道图中每个节点的访问概率和每个群组的跳转概率。其中访问概率的计算方法，Infomap 采取了类似 pagerank 的做法。1）初始所有节点都是均匀访问概率。2）在每个迭代步骤里，对于每个节点? 有2种方式跳转：要么以 1-r 的概率从节点 a 的连接边中选择一条边进行跳转，选每条边的概率正比于边的权重。要么以 r 的概率从节点 a 随机的跳到图上其他任意一点。3）重复步骤 2 直到收敛。

4 结语

将数据中台、智能风控等技术与供应链金融进行有机整合，使该平台可以在提供安全、可控的产业链金融服务的同时，也可以通过数据中台与各客户的自有信息化系统进行有效对接，让该平台具有更好的扩展性，具有更加广阔的应用领域。

参考文献

[1]Blondel VD，Guillaume JL.Fast unfolding of communities in large networks[J].Journal of Statistical Mechanics Theory & Experiment，2008（15）：2.

[2]Rosvall M，Axelsson D，Bergstrom CT.The map equation[J].The European Physical Journal Special Topics，2009（3）：15-18.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。