《非线性方程的数值解法中的二分法》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

非线性方程的数值解法中的二分法

范文

何天荣

摘要：代数方程的求根问题是一个古老的数学问题，早在16世纪就找到了三次、四次方程的求根公式。但直到19世纪才证明高于5次的一般代数方程式不能用代数公式求解。因此，需要研究用数值方法求得满足一定精度的代数方程式近似解。本文就二分法的理论、方法、例题方面进行阐述。

关键词：非线性方程；数值解法；二分法

1 二分法的理论依据

定理1[ 1 ] （1）设f（x）于[a，b]上连续；（2）且f（a）·f（b）<0，则存在x*∈（a，b）使f（x*）=0，即f（x）在（a，b）内存在实的零点。

定理1的理论依据来源于数学分析闭区间上连续函数的介值性定理。叙述如下：

定理2（介值性定理）[ 2 ] 设函数f（x）于[a，b]上连续，且f（a）≠f（b）。若？滋为介于f（a）和f（b）之间的任何常数（f（a）<？滋？滋>f（b）），则至少存在一点x0∈（a，b），使得f（x0）=？滋。定理的证明参见[2]，而定理1称为根的存在性定理，它是介质定理的特殊情况，即假设f（a）>0，f（b）<0或f（a）<0，f（b）>0情况下的介质定理中f（x）=0的结论。

2 二分法的过程叙述

设有非线性方程f（x）=0，其中，设f（x）为[a，b]上的连续函数且设f（a）·f（b）<0，用二分法求方程在（a，b）内的实根的过程，就是将含根区间逐步分半，检查函数值符号的变化，以便确定含根的充分小区间。具体做法是：记a1=a，b1=b。

第1步分半计算（k=1）：

于是得到长度缩小一半的含根区间

第k步分半计算：

重复上述过程，设已完成第1步、…、现进行第k步分半计算：

总之，由上述二分法得到一序列；可用二分法求方程f（x）=0实根到任意指定的精度。

事实上

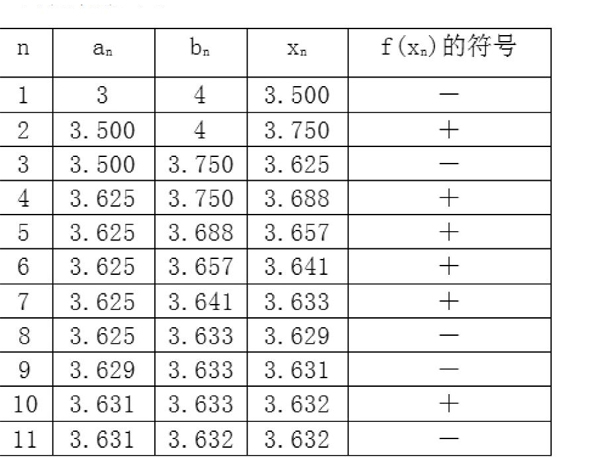
例插用二分法求方程x3-2x2-4x-7=0在区间[3，4]内的根，精确到10-3，即误差不超过

解：因为f（3）=-10<0，f（4）=9>0，

所以，方程在区间[3，4]上有根。

所以n=11，即只需要二分11次即可。

列表讨论如下：

参考文献：

[1] 易大义，沈云宝，李有法编.计算方法（第二版）[M].浙江大学出版社，2012.

[2] 华东师大数学系编.数学分析（第三版）[M].北京：高等教育出版社，2010.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。