《高等数学中的几个实验案例》-理学论文，数学论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

高等数学中的几个实验案例

范文

周琴

【摘要】本文设计了高等数学课程中的几个数学实验案例，内容涵盖极限、导数、积分等方面.对实验设置进行了分析，展示了MATLAB软件实验中的作图和计算过程.这些实验的完成有助于学生理解和掌握这些重要概念.

【关键词】极限;导数;积分MATLAB

【基金项目】2017年湖南涉外经济学院教学改革研究项目“数学实验在地方本科院校非数学专业教学中的应用研究”.

一、引言

高等数学是我校经管类、理工类等专业学生的必修课程，课程内容包括函数的极限、导数、积分等几大模块.运用数形结合思想能很好地解释有些类型的计算问题，但有些函数的直观图形描绘起来比较复杂，且不精确.而数学软件MATLAB具有强大的图形功能和符号计算功能，能较精确地描绘函数图像，并有专门的计算极限、导数、积分的函数.因此，运用MATLAB软件进行数学实验，有利于数形结合思想更好地运用.本文针对高等数学课程的几类重点、难点问题，设计了相应的实验案例.

二、实验案例

实验一设函数f（x）=1+2x，x<0，2，x=0，1-x，x>0.? 利用MATLAB作出该函数在[-2，2]的图像，观察f（0+0），f（0-0），limx→0f（x）的结果.

实验过程及分析：本题考查分段函数在分段点的极限计算.函数在某一点的极限指自变量无限接近该点时函数逼近的值.此题计算中，学生容易将0点的极限与函数值f（0）=2混淆起来，得到极限为2的错误结论.利用MATLAB软件作出该函数图像，主要的代码为

x=-2：0.1：0;y=1+2*x;plot（x，y，′r′）;hold on;x=0：0.1：2;y=1-x;plot（x，y，′r′）;hold on;x=0;y=2;plot（x，y，′r.′）;hold on;

x=0，y=1处的空心点绘制可由语句x=0;y=1;plot（x，y，′ro′）实现.得到的图形如图1所示.由图1可以清楚地观察f（x）在0点的左右极限情况.显然，f（0+0）和f（0-0）均为1，根据极限定义，此时 limx→0f（x）=1，而与0点的函数值2无关.

图1

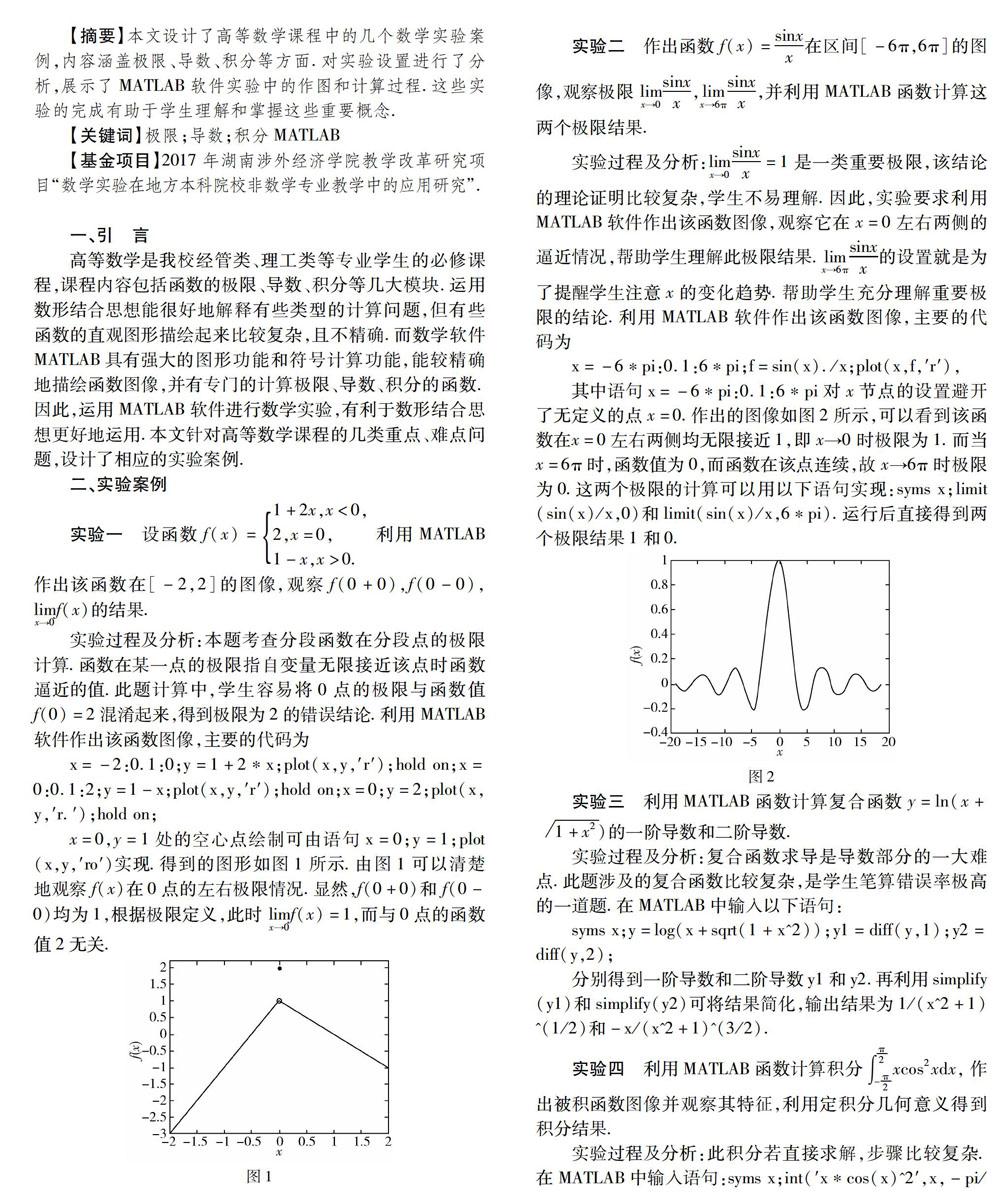
实验二作出函数f（x）=sinxx在区间[-6π，6π]的图像，观察极限 limx→0sinxx，limx→6πsinxx，并利用MATLAB函数计算这两个極限结果.

实验过程及分析：limx→0sinxx=1是一类重要极限，该结论的理论证明比较复杂，学生不易理解.因此，实验要求利用MATLAB软件作出该函数图像，观察它在x=0左右两侧的逼近情况，帮助学生理解此极限结果.limx→6πsinxx的设置就是为了提醒学生注意x的变化趋势.帮助学生充分理解重要极限的结论.利用MATLAB软件作出该函数图像，主要的代码为

x=-6*pi：0.1：6*pi;f=sin（x）./x;plot（x，f，′r′），

其中语句x=-6*pi：0.1：6*pi对x节点的设置避开了无定义的点x=0.作出的图像如图2所示，可以看到该函数在x=0左右两侧均无限接近1，即x→0时极限为1.而当x=6π时，函数值为0，而函数在该点连续，故x→6π时极限为0.这两个极限的计算可以用以下语句实现：syms x;limit（sin（x）/x，0）和limit（sin（x）/x，6*pi）.运行后直接得到两个极限结果1和0.

图2

实验三利用MATLAB函数计算复合函数y=ln（x+1+x2）的一阶导数和二阶导数.

实验过程及分析：复合函数求导是导数部分的一大难点.此题涉及的复合函数比较复杂，是学生笔算错误率极高的一道题.在MATLAB中输入以下语句：

syms x;y=log（x+sqrt（1+x^2））;y1=diff（y，1）;y2=diff（y，2）;

分别得到一阶导数和二阶导数y1和y2.再利用simplify（y1）和simplify（y2）可将结果简化，输出结果为1/（x^2+1）^（1/2）和-x/（x^2+1）^（3/2）.

实验四利用MATLAB函数计算积分∫π2-π2xcos2xdx，作出被积函数图像并观察其特征，利用定积分几何意义得到积分结果.

实验过程及分析：此积分若直接求解，步骤比较复杂.在MATLAB中输入语句：syms x;int（′x*cos（x）^2′，x，-pi/2，pi/2），即可得到积分结果为0.利用以下语句作出被积函数图像：

x=-pi/2：pi/40：pi/2;f=x.*cos（x）.^2;plot（x，f，′r′）;fill（x，f，′r′）;

图3

结果如图3所示.fill函数用于填充该曲线与x轴所围部分，显然被积函数为奇函数，x轴上方与下方面积相等.由定积分的几何意义，∫π2-π2xcos2xdx表示x=-π2，x=π2，y=0，y=xcos2x所围成的图形面积，在x轴上方面积取正，x轴下方面积取负，正负抵消即得该积分结果为0.

以上实验要求学生利用MATLAB软件作出函数图像，直观地展示函数特点，观察函数的极限及特殊函数的定积分结果.同时，利用MATLAB符号计算功能获得函数的极限、导数和定积分结果.通过学生自己动手来探索数学规律，提高学生的学习参与度，有助于强化这些重要知识点，培养学生对高等数学学习的积极情感.

【参考文献】

[1]同济大学数学系.高等数学：第7版[M].北京：高等教育出版社，2014.

[2]刘卫国.MATLAB程序设计教程：第2版[M].北京：水利水电出版社，2010.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。