《矩形基础受三角形分布荷载作用下中心位置附加应力简易算法》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

矩形基础受三角形分布荷载作用下中心位置附加应力简易算法

范文

胡红亮王玉丽

摘要：矩形基础受三角形分布荷载作用下，地基土中心位置下某点附加应力可以用常规方法“角点法”来计算，但是计算步骤较多，略显复杂，本文介绍了一种简易算法，并通过原理分析和实例计算对比，验证了此方法的正确性，并且计算结果较“角点法”精度更高。

关键词：矩形基础；三角形分布荷载；角点法；附加应力

1 概述

法国数学家布辛奈斯克（J.Boussinesq，1985）提出，如果有一个竖向集中力作用在弹性半空间表面上时，半空间内任意点处所引起的应力和位移可以应用弹性力学进行解答。在附加应力计算时，通过叠加原理或者积分的方法可以求得各种分布荷载作用时的土中应力计算公式。

例如，当有竖直三角形分布荷载作用在矩形基底时，取坐标原点为荷载强度为零的角点o，利用公式沿着整个面积进行积分即可求得，如图1所示。

以上公式（1-2）、（1-3）仅适用于角点下附加应力计算，其它位置需要根据《建筑地基基础设计规范》给出的附加应力系数表，采用“角点法”，并根据叠加原理进行计算。

2 “角点法”计算实例

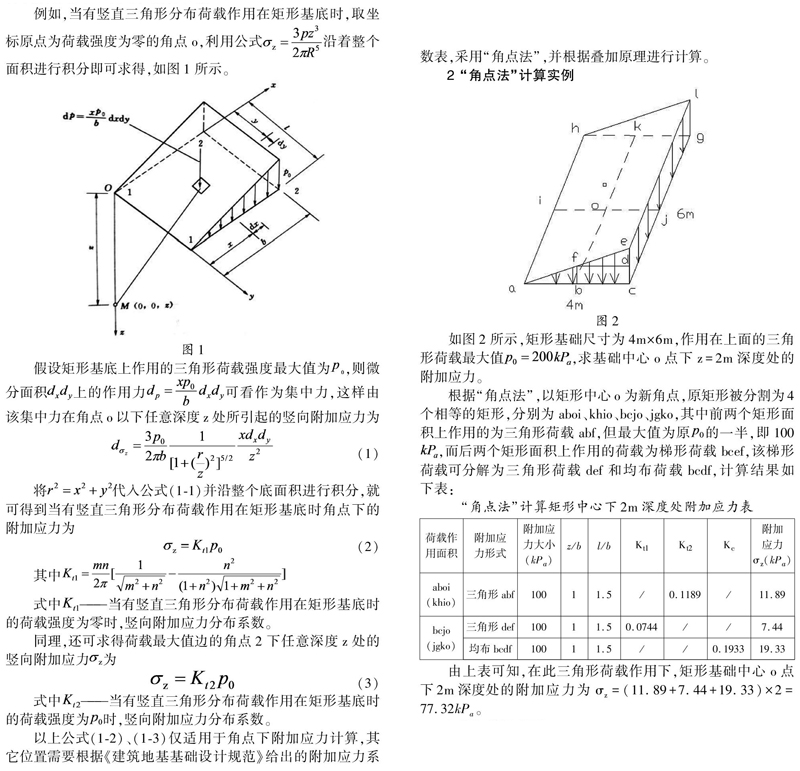
如图2所示，矩形基础尺寸为4m×6m，作用在上面的三角形荷载最大值，求基础中心o点下z=2m深度处的附加应力。

根据“角点法”，以矩形中心o为新角点，原矩形被分割为4个相等的矩形，分别为aboi、khio、bcjo、jgko，其中前两个矩形面积上作用的为三角形荷载abf，但最大值为原的一半，即100，而后两个矩形面积上作用的荷载为梯形荷载bcef，该梯形荷载可分解为三角形荷载def和均布荷载bcdf，计算结果如下表：

3 简易算法实例

为简化矩形面积上三角形分布荷载作用下地基中心下某点的附加应力计算，针对图2中作用的三角形分布荷载ace，我们假设该矩形面积上同时承受一个对称的三角形分布荷载acd，根据上述“角点法”计算实例，同样通过其中心点可拆分为四个面积相等的小矩形，由对称性可知，此三角形分布荷载acd对矩形中心下某點的附加应力与三角形分布荷载ace产生的附加应力是相同的，即三角形分布荷载ace产生的附加应力是叠加后总附加应力值的一半。而两个对称的三角形分布荷载叠加后的荷载等效于荷载值为原三角形分布荷载最大值的均布荷载，如图3所示。据此，我们可由z/b=1，l/b=1.5在GB50007-2011中查得Kc=0.1933，故可快速得到上述矩形面积上三角形分布荷载作用下地基中心下2m深度处的附加应力为σz=1/2（P0×Kc×4）=1/2（200×0.1933×4）=77.32kPa。

4 结语

通过上述实例对比可知，在三角形作用荷载下，采用常规“角点法”和简易计算法计算矩形基础中心下某点深度处的附加应力结果几乎一致，这验证了简易计算法的准确性，而且，由于简易计算法不需要将荷载形式进行分解，中间过程少，减少误差累计，计算结果较“角点法”精度更高。

参考文献：

[1]中华人民共和国住房和城乡建设部.GB50007-2011建筑地基基础设计规范[S].北京：中国建筑工业出版社，2012.

[2]陈仲颐，周景星，王洪瑾.土力学[M].北京：清华大学出版社，1994.

作者简介：胡红亮，江西南昌人，硕士，讲师；王玉丽，江西南昌人，硕士，助理讲师。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。