《基于GARCH族模型的深证指数波动性研究》-经济学论文，商业论文-论文范文参考-科学狗论文网

标题

基于GARCH族模型的深证指数波动性研究

范文

廖欣昱李喜梅古雨禾张天立

摘要：GARCH族模型是对金融数据波动性进行描述的有效方法。本文采用Eviews软件，选取2018年1月2日—2019年12月31日的深圳综指数共465个日收盘价，对数据预处理并转化为平稳的对数收益率序列，检验出ARCH效应之后对其定阶，最后基于建立GARCH和TGARCH模型分析其波动的特征，得出深证指数具有较高的波动集群性特征和杠杆效应，存在极端价格的变动情况，即股票市场还不够成熟并根据变动特征提出相应的政策建议，以供参考。

关键词：GARCH;TGARCH;波动集群性;杠杆效应;深证指数

中图分类号：F832.5 文献标识码：A 文章编号：2096-0298（2021）04（b）--04

股票市场是我国资本市场的重要组成部分，也是我国经济状况的“晴雨表”，对经济的走势和发展有巨大的预示作用和显著的推动作用。一般来说，股票市场价格上扬，交易活跃，是与整体国民经济的向好态势相呼应的。但是与发达国家相比，我国的股票市场尚不成熟，尤其是我国股市经常出现异常波动，这说明我国股市较不稳定，所隐藏的风险也较大。对我国股市来说，在宏观层面，容易受到经济周期的影响;在微观层面，也会受期望和个体行为等因素影响。因此，我们有必要对我国股市的波动情况进行研究。

本文选取深证综指价格指数，运用GARCH族模型对我国股市的波动规律进行分析，从而发现其波动特征，可以为投资者进行买卖决策提供重要的参考价值。

1 模型简介

1.1 ARMA模型

ARMA模型在时间序列的分析中最为常见，由自回归AR模型与滑动平均MA模型两部分混合构成。ARMA（p，q）模型中包含p个自回归项和q个移动平均项，ARMA（p，q）模型可以用以下公式表示：

（1）

1.2 ARCH模型

ARCH模型即自回归条件异方差模型，它的基本思想如下：若一个平稳随机变量xt可以表示为AR（p）模型，且其随机误差项的方差可以用误差项平方的q阶分布滞后模型来表示：

（均值方程）

（ARCH方程）

则由式（1）构成的模型被称为ARCH模型，记为ARCH（q）。其中{εt}为独立同分布的白噪声过程，且有E（εt）=0，D（εt）=。

1.3 GARCH类模型

1.3.1 GARCH模型

当滞后阶数q很大时，若继续使用ARCH模型来拟合数据会增加参数估计的难度，同时影响拟合的精度。为更好地处理高阶自回归问题，通常采用广义自回归条件异方差模型，即GARCH模型，其结构如下：

（均值方程）

（GARCH方程）

则定义上述随机过程{εt}服从GARCH（p，q）过程。同ARCH模型类似，其中{εt}为独立同分布的白噪声过程，且有E（εt）=0，D（εt）=。

1.3.2 TGARCH模型

TGARCH模型又称门限自回归条件异方差模型，是ARCH 模型非对称的一种形式，一般适用于剧烈波动的金融时间序列。本文主要采用TGARCH（1，1）模型，其条件方差方程的形式为：

其中，虚拟变量dt-1={1，0}，若，则取值为1，否则取值为0。

当时，，则方程可变为根据方程可知，利空的信息则会造成倍的冲击。

当时，，则方程可变为。

即利好的消息會对波动带来α的冲击，若，说明波动具有杠杆效应。

2 样本选取和数据预处理

本文选取深圳证券交易所2018年1月2日—2019年12月31日深证指数的日收盘价格，所有的数据均来源于网易财经。

根据单位根检验结果可以看出，在1%、5%、10%三种不同的置信水平下，收盘价序列的P统计量均大于0.05，故确定了原序列的不平稳性。为消除序列的不平稳性，考虑对深证指数日收盘价进行取对数，并进行差分处理，处理后的序列即对数收益率序列，可得隔夜收益率：

其中St表示t时刻的收盘价，表示St-1时刻的收盘价，ds表示对数收益率。对收益率序列作平稳性检验，根据时序图可以看出，处理后的序列是围绕0处上下波动的高频数据，初步判定收益率序列为平稳序列。

3 数据描述及分析

3.1 描述性统计

利用Eviews软件对深证指数对数收益率序列的描述统计结果，如表1所示。

根据数据显示收益率序列的中位数大于其均值，说明其右偏;正态分布的偏度等于0，峰度等于3;该序列偏度为负值，说明有较长的左拖尾;峰度K=5.386621，说明收益率分布相比于正态分布更具有“尖峰”，即存在尖峰厚尾;Jarque-Bera统计量的P值拒绝了服从正态分布的原假设，说明了深证指数的日收益率序列不服从正态分布。

3.2 单位根检验

对收益率序列进行ADF检验，即有趋势项和截距项、只有截距项、无趋势项和截距项这三种，用以检验数据的平稳性，其检测结果如表2所示。

结果显示，在1%、5% 和10%的置信水平下，三种形式下的序列均平稳。其中，带Intercept形式的截距项P统计量不显著，Intercept&Trend形式的截距项和趋势项的P统计量均不显著，故判断该收益率是None形式的平稳序列。

4 模型的定阶和构建

4.1 模型的识别和定阶

基于平稳序列，可以看出深证指数收益率序列的自相关（ACF）和偏自相关（PACF）图均没有明显的拖尾和截尾现象，故尝试建立ARMA模型。

根据相关函数和自相关函数图，ACF和PACF在三阶有略微显著的倾向，故判断AR过程和MA过程为1-3阶，采用最小二乘法，使用Eviews进行建模，尝试将ARMA（p，q）中p，q阶分别历遍1～3阶，共九个模型，各项的P统计量即显著性整理如表3所示。

由表3可以看出，只有ARMA（1，1）模型的变量均显著，其他模型均含有不显著的项，不适用于收益率序列，故确定模型的阶数为ARMA（1，1）。

4.2 ARCH效应检验

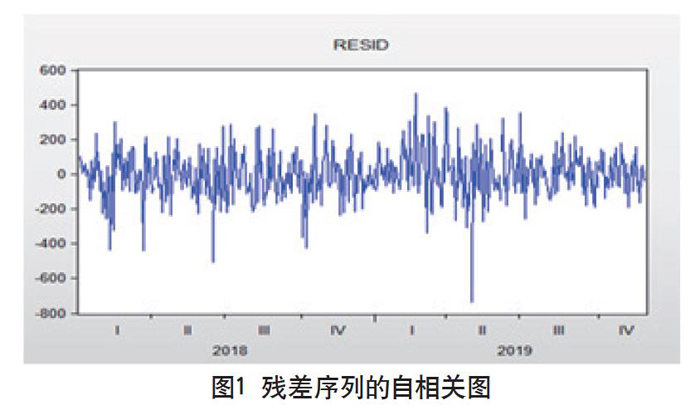
由上文可知，ARMA（1，1）模型具有最优的拟合效果。因此我们选择建立ARMA（1，1）模型，然后运用ARCH-LM检验来确定序列是否存在异方差性，残差序列的自相关图如图1所示。

由图1可知，残差序列表现出明显的波动聚集性，说明残差序列可能具有异方差性。ARCH-LM检验的原假设是：不存在ARCH效应。在进行ARCH-LM检验时，对滞后阶数1～10进行ARCH检验，根据检验结果的信息准则，通过分析比较发现，滞后4阶的参数系数都较小，因此选择ARCH（4）。

此时其检验结果为：深证成指收益率DS的F检验统计量的值为2.577368，P值为0.0369，小于0.05，因此在5%的显著性水平下拒绝没有ARCH效应的原假设，即ARMA（1，1）模型具有显著的ARCH效应。所以我们选择GARCH模型对深证成指的日收益率序列进行建模分析是合理的。

5 实证分析

因为从上述检验结果证实深证指数日收益率序列的残差中存在ARCH效应，因此可以应用GARCH模型进一步分析。

5.1 GARCH模型定阶

在研究金融时间序列时，使用GARCH模型最常用的模型有GARCH（1，1）、GARCH（1，2）、GARCH（2，1）、GARCH（2，2）。在上述的描述性统计中，发现深证指数收益率序列有“尖峰厚尾”的特征，不服从正态分布，因此考虑残差服从t分布或者GED分布假设。经过AIC检验可以发现GED分布拟合效果不佳，故舍弃。考虑在t分布下模型的定阶，不同阶数的信息准则结果如表4所示。同时要考虑拟合结果的ARCH项和GARCH项系数不得小于零，各回归结果整理如表5所示。

根据表4、表5的数据对比信息准则和负数值可以看出：GARCH（1，1）显然比其他几个模型更适合收益率序列，拟合效果最佳。故选择GARCH（1，1）进行建模分析。

5.2 GARCH模型

经上述分析后，已确定模型的滞后阶数，接下来建立服从t分布的GARCH（1，1）模型。运用Eviews10 统计软件进行回归，拟合后的模型为：

均值方程：

方差方程：

回归模型的系数均有高度的显著性，在条件方差方程中，估计的GARCH系数（0.9019）远远大于ARCH系数（0.0506）。表明前一时期的波动性更加敏感。ARCH项系数大于0说明来自外界的冲击会增加日收益率的波动;ARCH和GARCH系数之和接近于1，说明了波动的持续性，表明在日收益率中存在均值回归方差过程。虽然冲击随时间衰减，受外界因素的影响具有长效性。两项之和小于1，在参数设置上达到要求，可以预测未来的走势。

为了进一步检验ARCH效应是否还存在于所建立的GARCH（1，1）模型中，我们对模型残差进异方差检验，由ARCH-LM检验结果可知，F统计量为0.778289，相应的P值为0.6499，拒绝了存在ARCH效应的原假设。说明残差序列不再存在ARCH效应，即GARCH 模型消除了DS残差序列的异方差性。

5.3 T-GARCH模型

为进一步研究外界冲击对于深证综指日收益率序列DS的非对称效应，在上述建立GARCH（1，1）模型的基礎上，建立TGARCH （1，1）模型并进行分析估计。该模型的均值方差方程如下：

均值方程：

方差方程：

信息准则结果显示AIC=12.68163，SC=12.73525，且差分方程中的常数项系数、ARCH项系数和GARCH项系数的统计量均显著。表明所建模型对样本的拟合度很好。方差方程中，ARCH项大于0，说明利好信息会对日收益率序列产生正向冲击;ARCH项系数和GARCH项系数之和为0.9431，非常接近于1，说明利用此模型进行预测时的精度高。

从TARCH（1，1）模型估计结果来看，非对称性项系数的估计值为0.2052>0，说明该序列存在非对称影响，也就是说“杠杆效应”在我国深证综指的波动性中显著存在，即利好消息和利空消息对条件方差产生不同程度的冲击。

由TGARCH（1，1）模型估计的具体参数可得：

出现利好消息即时，有，此时利好消息会对上证指数有一个α=-0.0286倍的冲击，而出现利空消息即时，有，此时会对深证综指带来倍的冲击。比较可得，利空消息对深圳综指波动带来的影响大于利好消息的影响，因此深证综指收益率具有非对称性。

接下来对TGARCH（1，1）模型对残差进行ARCH-LM检验，检测其是否消除了ARCH效应。在进行检验时，选择1～10阶滞后阶数进行ARCH检验，根据结果可知：F统计量的p值均大于0.05，在5%的显著性水平下，不拒绝不存在ARCH效应的原假设，说明TGARCH（1，1）模型消除了残差序列的异方差效应。

综上所述，TGARCH（1，1）模型较好地消除了方程残差的ARCH效应，同时验证了深证综指波动具有杠杆性。

6 结论及建议

6.1 结论

本文选取中国股票市场的深证综指作为样本数据，通过Eviews10统计软件，建立ARMA—GARCH模型对深证综指日收益率序列进行实证分析，旨在研究我国股票市场波动特征，得到结论如下。

（1）从深证综指收益率的基本描述性统计来看，收益率序列是平稳序列，但股指峰度大于3，偏度为负值，呈现出尖峰厚尾的特征，不服从正态分布。峰度较大，说明股票市场波动较为剧烈，容易产生极端性的变动;偏度为负，说明收益率很可能出现大幅度下降的情况。这反映出我国股票市场还不够成熟，市场风险较大。

（2）深证综指收益率序列没有明显的线性趋势，而是表现出显著的波动集聚性、“尖峰厚尾”特征和非正态性分布性，同时具有异方差效应，所以采用非对称性的GARCH类模型对股指收益波动进行实证研究，可以更好地分析其非对称性。

（3）在利用TGARCH和EGARCH的非对称研究中，我们发现深证综指存在显著的“非对称性效应”，表现为“杠杆效应”，即同等程度下，“利空消息”对股市波动的影响大于“利好消息”。

6.2 建议

价格指数的波动意味着收益和风险的不确定性，本文通过实证研究，我国的股票市场仍存在着波动剧烈等问题，易产生较大风险，因此提出以下发展建议。

（1）做好信息披露，减少政府干预。信息不对称会带来很多问题，如逆向选择和道德风险等，信息披露可以减少信息不对称带来的影响，减少利益失衡现象。政府应适当地进行宏观调控，但是应该尽可能地将利率等定价权交给市场，这样会让股市经济健康发展。

（2）丰富我国金融衍生品。金融衍生品可以完善我国金融市场体系，且在规避风险、套期保值等方面具有重要作用，对我国金融市场的稳定也有着重要作用，此外，还有助于提高金融创新能力。

（3）完善风险管理制度。为了保护投资者在投资过程中的合法利益，需要完善风险管理制度，如建立健全风险保证金制度、实行第三方资金托管、强制涨跌制度等，尽量规避风险。

参考文献

宋小宇，侯为波.基于GARCH模型的上证指数波动性实证分析[J].淮北师范大学学报（自然科学版），2019，40（02）：19-24.

洪绍应，张青龙.猪肉板块指数的波动性分析及预测——基于ARMA-GARCH模型[J].中国物价，2019（11）：81-84.

顾程铭，杨开奇，余骆麟，等.GARCH模型在研究上证50指数基金收益率上的运用[J].时代金融，2020（02）：72-73.

陈研研.中国股票市场的节日效应研究[D].太原：山西大学，2019.

徐莹.基于GARCH模型族的我国A股行业板块月份效应研究[D].苏州：苏州大学，2019.

章维.基于GARCH类模型对人民币汇率波动的实证研究[D].武汉：武汉大学，2019.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。