《一种新的暴雨公式参数推求方法》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

一种新的暴雨公式参数推求方法

范文

荆燕燕庞正崎

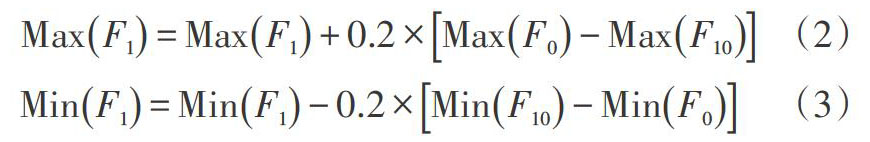
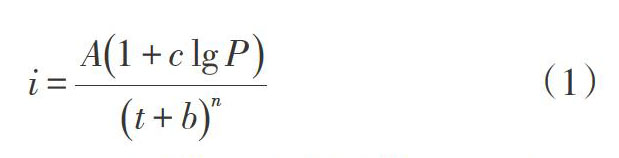
摘要：本文针对暴雨公式参数推求方法，设计了一种新的推求方法。该法以暴雨公式参数经验范围为基础，逐步缩小范围，在一定范围内随机搜索最优解。在不需要复杂数学知识情况下，该方法单纯依靠计算机强大的运算能力，获得暴雨公式参数值。经试验证明，该方法在可行范围内可以获得精确参数。

关键词：倍比搜索法;MATLAB;暴雨公式参数

中图分类号：P426.6文献标识码：A文章编号：1003-5168（2018）32-0013-02

A New Method of Parameter Estimation for Rainstorm Formula

—— Double Ratio Search Method

JING Yanyan1 PANG Zhengqi2

（1.Henan Vocational College of Water Conservancy and Environment，Zhengzhou Henan 450045;

2.North China University of Water Resources and Electric Power，Zhengzhou Henan 450045）

Abstract： In this paper， a new method of derivation was proposed for the method of parameter estimation of rainstorm formula. Based on the empirical range of storm parameter parameters， this method gradually narrowed the range and randomly searches for the optimal solution within a certain range. Without complicated mathematical knowledge， the method relied solely on the powerful computing power of the computer to obtain the parameter value of the storm formula. The test proved that the method could obtain accurate parameters within the feasible range.

Keywords： ratio search method;MATLAB;rainstorm formula parameters

暴雨公式參数推求方法主要分为两种，即解析法和算法。解析法包括麦夸尔特法、遗传算法、高斯-牛顿法和二次优化算法等，这些算法可准确求出解值，但在暴雨公式参数推求中求得的解具有一定随机性;算法解则是利用计算机程序进行求解，求出的多是近似解。本文提出的倍比搜索法属于算法解范畴[1]。

现代水文计算中，已经普遍采取计算机辅助计算。但是，要想理解解析算法，还是需要水文工作者自身具备相当的数学应用能力，并在此基础上进行编程。换句话说，暴雨公式参数推求不仅对数学知识有较高要求，而且对编程也有一定的要求。如果存在一种仅依靠编程算法就可以得出最优解的方法，将会大大降低算法难度。

1 倍比搜索法基本原理

根据《给排水设计手册》中所述，城市短历时暴雨计算公式如式（1）所示。

[i=A1+clgPt+bn]? ? ? ? ? ? ? ? ? ? ? ? ? ?（1）

式中：[i]为雨强，[P]为重现期，[t]为相应降雨历时，A、c、n、b为待推求参数。

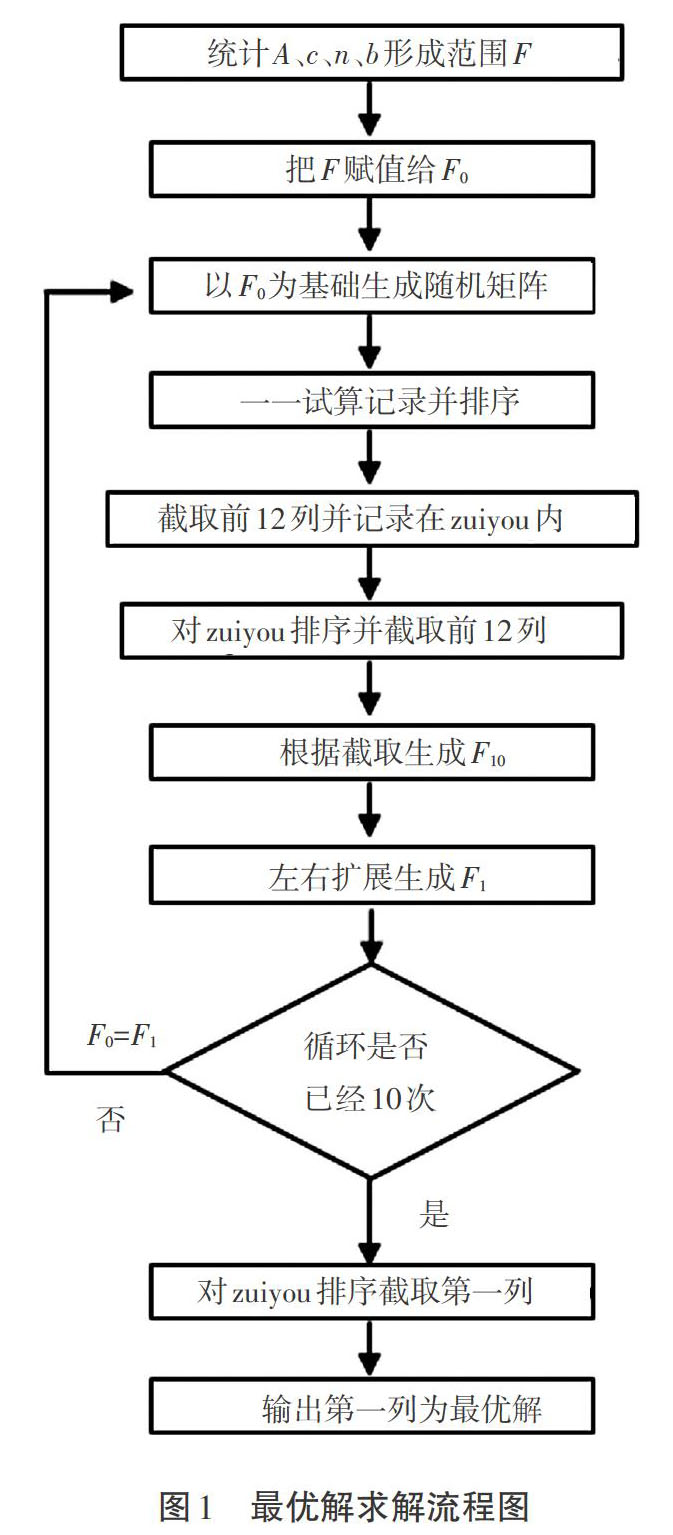
对于已经进行过适线处理的数据，可以得到由降雨时间t、降雨强度[i]和降雨强度对应重现期[P]所组成的数据矩阵。统计地区周边地区的暴雨公式，统计得出4个参数A、c、n、b的经验范围，再适当扩展4个参数经验范围，最终得到初始范围[F0]。

在[F0]范围基础上，随机生成上万个解向量，然后一一试算、记录、排序，取若干列次优结果。这些若干组次优解的4个参数均有自己的范围，这个范围是过渡范围[F10]。为了尽可能保证最优解在试算范围内，对过渡矩阵[F10]两侧按一定倍比向外侧延展得到倍比范围[F1]，然后把[F1]看作初始范围[F0]，回到本段段首开始循环[2]。

暴雨公式在数学上是一个连续函数。所以，通过搜索最优解所在区域，再通过扩展倍比，即可保证最优解一定在新生成范围内。随着试算循环的进行，倍比范围一步步缩小，而试算随机解向量的各个参数也会逐渐逼近最优参数。当循环达到一定的次数，解向量即可达到较高精度。

2 算法实现的程序过程

本文使用数学编程工具MATLAB，并利用经典的向量化思想，以矩阵为单位来实现编程。

首先，调查周边地区暴雨资料，统计A、c、n、b的范围，适当扩大得到初始范围F。同时，整理适线过的暴雨资料，作二维i-p-t数据矩阵，并输入MATLAB[3]。

其次，进行准备工作。生成一个空矩阵zuiyou，用于记录后期每次循环过程产生的次优解，把F赋值给[F0]，根据[F0]的4个参数范围，生成一个5行20 000列的随机范围矩阵，其中第一行的值是在A经验范围内的随机值，后面，3列c、n、b类同，第5行为预留空间，用于记录[σj]。

再次，取随机范围矩阵第一列作为A、c、n、b的值代入暴雨公式，相应计算i-p-t数据矩阵的[σj]，记录在此列第5行，依次算得余下各列对应[σj]。同时，对此5行20 000列矩阵按[σj]（第5行）从小到大排序，然后截取前10列数值，把此10列增补记录于矩阵之中。

最后，按第5行对最优解排序，截取前10列。统计此10列前4行A、c、n、b范围，生成过渡范围[F10]。过渡范围[F10]是初始范围[F0]的各参数组成的一维坐标内的一块区域。为了确保最优解包含在内，按一定的倍比q对[F10]作适当扩展。用参数A来说明，具体方法是用A向两侧延伸，A范围具体实现方法如式（2）、式（3）所示。

[MaxF1=MaxF1+0.2×MaxF0-MaxF10]? ?（2）

[MinF1=MinF1-0.2×MinF10-MinF0]? ? ?（3）

c、n、b按照此法依次处理，就生成了新的范围[F1]。把[F1]赋值给[F0]，开始循环。一般情况下，14次循环后即可得到可以接受的解，第5行排序第一列为最优解，算法结束，具体流程如图1所示。

在上述最优解求解过程中，需要注意以下几点问题：第一，每次截取个数n为10，建议n值为10～20;第二，随机范围矩阵列数m应为n的1 500倍以上;第三，为了优化算法，前2次循环可取4 000倍，后续循环取1 500倍甚至更小;第四，向两侧扩展的倍比q建议为0.15～0.3之间，其是确保最优解在范围内的关键，不可太小，否则可能错过最优解，造成算法不稳定;第五，循环次数应大于10，数据实验表明，14次循环结束时，各参数范围均缩小到不足原来的1/800[4]。

3 结论

通过以上分析可得，倍比搜索法以计算机编程为基础，一方面数学难度非常小、编程难度小，另一方面對公式也没有特殊要求，并可将平均绝对均方差控制在5mm/min。该方法不仅适用于单个重现期计算，而且适用于多个重现期计算。与其他方法相比，倍比搜索法更加简单、精确和快速，实用价值高，适宜在水文计算中推广使用。

另外，倍比搜索法也可以用在其他类型参数求解问题上，仅需满足以下三个条件即可使用：第一，公式形态确定;第二，公式是由初等函数构成的连续函数;第三，各参数有模糊的经验范围。这表明此法对于其他多参数的推求也有普遍适用性。

参考文献：

[1]Musto J.C，Howard W.E，Williams R.R.An Introduce Using MATLAB and Excel[M].北京：清华水学出版社，2010.

[2]陈静，周志芳.一种新的水文地质参数优化方法——Tabu搜索法[J].水电能源科学，2005（3）：35-37.

[3]朱春龙，薄丽洁，王明生.确定多重现期暴雨公式参数的二次优化算法[J].水文，2012（4）：13-15.

[4]林齐，傅金祥.铁岭市暴雨强度公式的推求与优化[J].沈阳建筑大学学报（自然科学版），2006（4）：613-616.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。