《改进的卡尔曼滤波预测采煤工作面瓦斯涌出量》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

改进的卡尔曼滤波预测采煤工作面瓦斯涌出量

范文

唐一举

摘要：为了准确可靠预测工作面的瓦斯涌出量，本文以卡尔曼滤波为基础，结合人工神经网络，设计虚拟中间状态变量并得出对应预测模型。其間通过Matlab使预测模型实现目的，并用此方法对某矿采煤工作面瓦斯涌出量进行预测。结果表明，建立的预测方法具有较好的预测性能，其平均误差为3.35%，结果正确可靠。

关键词：卡尔曼滤波法;径向基神经网络;瓦斯涌出量

中图分类号：TD712.5文献标识码：A文章编号：1003-5168（2019）29-0096-03

Improved Kalman Filter for Predicting Gas Emission from Coal Face

TANG Yiju

（Henan College of Industry & Information Technology，Jiaozuo Henan 454000）

Abstract： In order to accurately and reliably predict the amount of gas emission from the working face， this paper used the Kalman filter as the basis and combined the artificial neural network to design the virtual intermediate state variables and obtain the corresponding prediction model. In the meantime， the prediction model was achieved by Matlab， and the gas emission from a coal mining face was predicted by this method. The results show that the established prediction method has better prediction performance， and the average error is 3.35%， the result is correct and reliable.

Keywords： Calman filtering method;radial basis function neural network;gas emission

煤矿瓦斯灾害严重影响煤矿的可持续生产，因此非常有必要对瓦斯涌出量进行精确预测，以保证矿井安全生产。长期以来，学者对瓦斯涌出量预测方法做了大量的研究，付华等采用ACC-ENN算法构建煤矿瓦斯涌出量动态预测模型[1]，樊保龙提出了基于LMD-SVM的采煤工作面瓦斯涌出量预测方法[2]，朱红青研究了基于人工神经网络的工作面瓦斯涌出量预测方法[3]，陶云奇通过改进的灰色马尔柯夫模型预测采煤工作面瓦斯涌出量[4]，这些瓦斯涌出量预测方法取得了一定成功。

采煤工作面的瓦斯涌出受地质赋存条件、煤层瓦斯含量、采煤方法、通风方式等众多因素的影响，这些因素相互影响。基于以上原因，如果利用固定的预测网络和参数来建立瓦斯涌出量预测方法，预测时很有可能出现不满足精度的结果。为了能够可靠连续地预测出矿井瓦斯涌出量，人们提出了一种改进的卡尔曼滤波预测方法，以便合理预测矿井瓦斯涌出量[5，6]。

1 卡尔曼滤波法的瓦斯涌出量模型建立

1.1 预测方法的建立

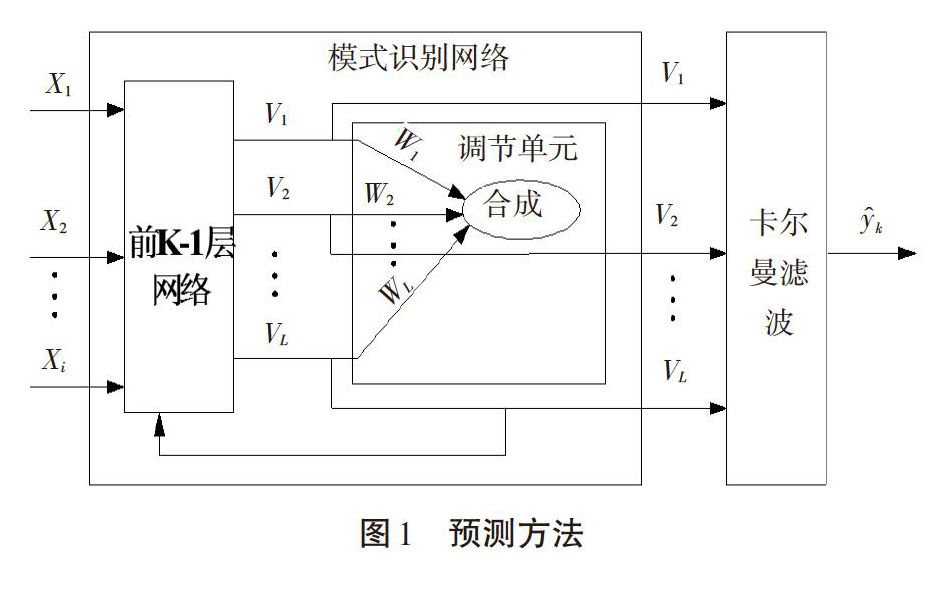
卡尔曼滤波预测方法利用状态空间方程进行预测，首先需要获取相应的状态方程和状态变量。但是，直接构建非线性系统的状态空间方程通常面临诸多困难，结合传统的人工神经网络方法，设计虚拟中间状态变量并得出对应状态方程。参照人工神经网络方法的特点，可定义虚拟的状态变量如下：将瓦斯涌出量相关因素输入神经网络中进行非线性映射，在输出节点之前可得到一些能够反映待识别对象特征的变量，这些变量被称为虚拟变量，记为[vi]。所有虚拟变量合起来构成的向量被称为虚拟状态变量[v]。结合所定义的虚拟状态变量，基于神经网络辨识的卡尔曼滤波预测方法的实现步骤如图1所示。

整个预测方法主要由两个部分组成：输入端的人工神经网络和输出端的卡尔曼滤波。影响瓦斯涌出量的各种因素[xi]作为输入变量进入人工神经网络，该神经网络由前[K]-1层网络和调节单元两个部分构成。前[K]-1层网络用于识别和生成虚拟变量;调节单元则由合成器和参数[wi]构成，用于合成瓦斯涌出量结果，并将合成结果与训练样本中的真实值进行比对后去调节前[K]-1层网络的结构和参数，从而得到最终的、合适的虚拟变量。随后，这些虚拟变量构成的虚拟状态变量被用于构建系统的状态空间方程，进行卡尔曼滤波递推运算，最终得到对瓦斯涌出量的精确估计值。

1.2 状态空间方程确定

卡尔曼滤波预测方法利用状态空间进行线性最优估计，首先需要构建系统的状态空间方程模型。在状态空间内，描述的离散线性动态系统通常包含一个状态方程以及一个输出方程（也称观测方程），即

[][vk+1=Akvk+Bkuk+ξk]? ? ? ? ? ? ? ? ? ? ? ? ?（1）

[yk=Ckvk+Dkuk+ηk]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（2）

式中，[v]为[n]维的状态向量;[u]为[m]维控制向量;[y]为[q]维的输出向量;[Ak]为[n]×[n]阶状态转移矩阵;[Bk]為[n]×[m]阶控制矩阵;[Ck]为[q]×[n]阶输出矩阵;[Dk]为[q]×[m]阶输出控制矩阵。一旦系统确定，上述矩阵也随之确定。然而，动态系统中除了上述已知量外，还往往包含未知的系统噪声[ξ]和观测噪声[η]，通常假定为零均值的高斯白噪声，方差为正定常值矩阵。

[E（ξ）=0var（ξ）=RE（η）=0var（η）=Q]? ? ? ? ? ? ? ? ? ? ? ? ? ? （3）

瓦斯涌出量受众多因素影响，是一个典型非线性特点的复杂系统。因此，在所定义虚拟状态变量的基础上，利用神经网络屏蔽最终预测值与众多影响因素之间的真实物理关系，将非线性系统转化为可用状态空间方法进行表述的线性动态系统。

首先根据分析，可得出基于神经网络条件下的系统输出方程：

[yk=Ckvk+ηk=ωk1? ωk2 … ωk3hk1hk2?hk3+ηk]? ? ? ? ? ? ? ? （4）

可见，这里的状态向量实质上是RBF网络中隐层节点的输出;输出矩阵则对应的是从隐层到输出层之间的权值矩阵。同时，考虑到整个瓦斯涌出量预测系统是一个缓慢变化系统，因此在较短的离散周期前提下，可假定当前时刻虚拟状态变量与上一时刻虚拟状态变量近似相等，即系统状态转移矩阵为单位阵，故而得系统状态方程：

[vk+1=Akvk+ξk=I·vk+ξk]? ? ? ? ? ? ? ? ? ?（5）

1.3 卡尔曼滤波实现

卡尔曼滤波包含校正和预测两个步骤。预测是利用系统的状态方程根据前一时刻的状态计算出现在时刻的状态：

[vkk-1=Ak-1vk-1k-1]? ? ? ? ? ? ? ? ? ? ? （6）

式中，上标[∧]表示有关参数为估计值;下标[k]/[k]-1代表[k]-1时刻对[k]时刻的预测;下标[k]-1/[k]-1代表第[k]-1时刻经过校正后的估计。一般情况下，利用式（6）对当前时刻状态的估计是不准确可靠的，因而需要结合当前时刻系统的实际输出进行校正修改。

[vkk=vkk-1+Gkyk-Ckvkk-1]? ? ? ? ? ? ? ? ? ? ? （7）

式中，[yk]为当前时刻的实际输出;[Ckvkk-1]为当前时刻的估计输出;[Ck]为卡尔曼增益矩阵，在实际应用中也必须递推计算。

从式（6）和式（7）可以看出，卡尔曼滤波的核心就是递推求取校正时所需要的卡尔曼增益矩阵，故而总结出整个卡尔曼滤波的实现过程如下。

首先，预测协方差矩阵，该协方差用于计算卡尔曼增益。其中，[Pkk-1]和[Pk-1k-1]分别为对应[vkk-1]和[vk-1k-1]的协方差矩阵;[Ak-1]为状态转移矩阵，假定其在瓦斯涌出量预测中作为单位矩阵;[Q]为方差矩阵。

[][Pkk-1=Ak-1Pk-1k-1ATk-1+Q]? ? ? ? ? ? ? ? ? ? ? （8）

其次，计算卡尔曼增益矩阵，该增益用于校正状态向量。其中，[Gk]为输出矩阵，在瓦斯涌出量预测系统中对应为神经网络的权值矩阵;[R]为方差矩阵。

[Gk=Pkk-1CTkCkPkk-1CTk+R-1]? ? ? ? ? ? ? ? ? ? ? ? （9）

再次，更新协方差矩阵，该方差用于下一次的预测协方差矩阵。

[Pkk=I-GkCkPkk-1]? ? ? ? ? ? ? ? ? ? ? （10）

第四，预测状态。

[vkk-1=Ak-1vk-1k-1]? ? ? ? ? ? ? ? ? ? （11）

第五，校正状态。

[vkk=vkk-1+Gkyk-Ckvkk-1]? ? ? ? ? ? ? ? ? ? ?（12）

最后，计算估计输出，代表对于瓦斯涌出量的最优预测。

[yk=Ckvkk]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（13）

2 卡尔曼滤波瓦斯涌出量动态预测模型构建及应用

2.1 瓦斯涌出量相关数据的采集

根据前面部分对影响工作面瓦斯涌出量因素分析建立的卡爾曼滤波模型，从中提取出13种影响因素，即煤层采深、煤层厚度、煤层间距、煤层倾角、开采高度、层间岩性特征、本煤层瓦斯含量、临近层瓦斯含量、临近层厚度、工作面长度、工作面推进速度、工作面采出率、日产量，作为预测模型的输入。

2.2 相关数据的归一化处理

为防止预测模型的神经元输出饱和，导致权值调整进入误差曲面的平坦区域，须令BP网络模型的样本数据尽可能保持在[0，1]。因此，必须对样本数据进行归一化处理：调用Matlab神经网络工具箱里的Premnmx函数，将样本数据归一化到[-1，1]，然后利用式（14）将数据归一化到[0，1]。

[X=0.5x+0.5]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （14）

式中，[X]为归一化后的数据;[x]为归一化到[-1，1]的样本数据。

2.3 实例分析

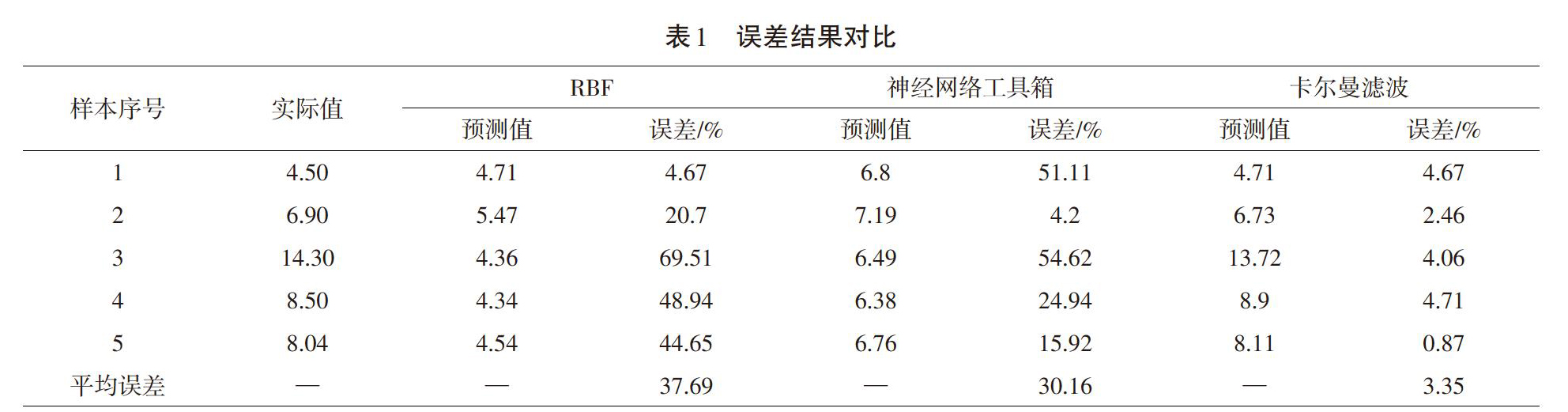
笔者选取某矿区回采工作面绝对瓦斯涌出量历史监测数据进行建模分析和预测，选取了几个对瓦斯涌出量影响较大的因素的历史数据作为预测模型的训练、测试样本集。采用神经网络、神经网络工具箱和卡尔曼滤波得出的预测结果以及去归一化后得出的结果，与实际测出的涌出量值对比，就可以得出各自的误差，结果如表1所示。

表1为传统的算法与卡尔曼滤波模型预测结果与实际值进行了比较，RBF平均误差为37.69%，神经网络工具箱平均误差为30.16%。卡尔曼滤波模型预测平均误差为3.35%，预测精度较好，具有较好的预测性，能够动态跟踪瓦斯涌出量变化。

3 结论

本研究构建了基于卡尔曼滤波的瓦斯涌出量预测模型，进行数据归一化处理，确定了状态空间方程，最终实现预测目的。同时，将得出预测结果与实测数据进行对比，结果表明，卡尔曼滤波瓦斯涌出量模型预测精度较好，具有较好的预测性，能够动态跟踪瓦斯涌出量变化。

参考文献：

[1]付华，谢森，徐耀松，等.基于ACC-ENN算法的煤矿瓦斯涌出量动态预测模型研究[J].煤炭学报，2014（7）：1296-1301.

[2]樊保龙，白春华，李建平.基于LMD-SVM的采煤工作面瓦斯涌出量预测[J].采矿与安全工程学报，2007（6）：946-952.

[3]朱红青，常文杰，张彬.回采工作面瓦斯涌出量BP神经网络分源预测模型及应用[J].煤炭学报，2007（5）：504-508.

[4]陶云奇，许江，李树春.改进的灰色马尔柯夫模型预测采煤工作面瓦斯涌出量[J].煤炭学报，2007（4）：391-395.

[5]何利文，施式亮，宋译，等.回采工作面瓦斯涌出量的复杂性及其度量[J].煤炭学报，2008（5）：547-550.

[6]王晓路，刘健，卢建军.基于虚拟状态变量的卡尔曼滤波瓦斯涌出量预测[J].煤炭学报，2011（1）：80-85.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。