两套教材中“生活中的圆周运动”实例比较

    陆学新

    

    

    

    [摘要]“生活中的圆周运动”一节，人教版普通高中新课程实验教科书选取“铁路的弯道”“拱形桥”等作为例子，沪科版教科书选取“分析游乐场中的圆周运动”（重点是过山车）“研究物体转弯时的向心力”（重点是自行车转弯）等为例文章用生活中的数据比较这些实例，分析谁更贴近学生的生活实际，更容易激发学生的学习热情。

    [关键词]自行车转弯;铁路的弯道;拱形桥;过山车;实例比较

    [中图分类号]

    G633.7

    [文献标识码] A

    [文章编号] 1674-6058（2020）17-0040-02

    在人教版普通高中新课程实验教科书“生活中的网周运动”一节选取“铁路的弯道”“拱形桥”等为实例，而沪科版则选取“游乐场中的网周运动”（重点是过山车）和“物体转弯时的向心力”（重点是自行车转弯）等为实例。

    一、自行车转弯与铁路的弯道比较

    1.自行车转弯

    在沪科版教科书“网周运动的案例分析”一节案例2“研究运动物体转弯时的向心力”是以自行车转弯为例来进行分析研究的。

    通常情况下我们在骑自行车转弯时，车和人会倾向弯道的内侧，这是什么原因呢？

    分析：设自行车转弯时轨迹（作为网周的一部分）的半径为R，人和自行车的总质量为m，自行车转弯时速率为v。

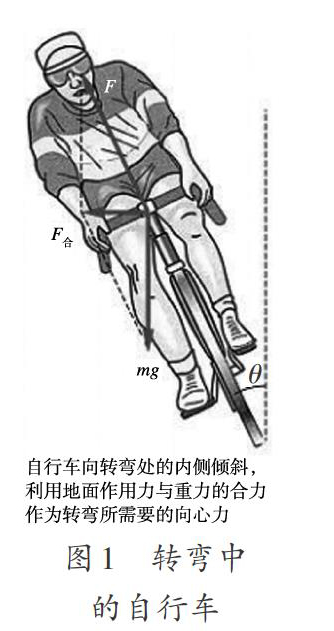
    自行车在转弯处的受力分析如图1所示，图1中的F是地面对车的作用力（地面对车的支持力和静摩擦力的共同作用效果），mg是重力，这两个力的合力F合就是自行车做圆周运动时的向心力，指向弯道处的同心。

    请思考并分析：自行车转弯时倾斜的角度与哪些因素有关？

    设自行车与竖直方向的倾角为θ，则F合=mg tanθ，又F合= mv2/R，联立得tanθ=v2/gR。可以看出，自行车转弯时倾斜的角度θ与速度v和弯道半径R有关，速度越大，半径越小，倾斜的角度越大。

    实际教学中，对人和自行车的整体进行研究时，还可以这样分析，人和车受到重力mg，地面对车的支持力FN地面对车的静摩擦力Ff作用，地面对车的静摩擦力Ff指向弯道网心，是人和车做圆周运动的向心力。由此思考并讨论，下雨天转弯时如何防止滑倒？

    由Ff= mv2/R知道，为防止滑倒，转弯时速度要小，弯道半径要大。

    現在公路建设标准都很高，弯道处都建成外高内低的路面，按设计标准速度行驶转弯，车受侧向摩擦力影响很小，更安全。由于公路弯道是按汽车设计标准速度设计的，自行车经过时（速度小于没计速度）需向上倾斜一些，不会垂直路面。

    2.铁路的弯道

    人教版教科书“生活中的圆周运动”以“铁路的弯道”为例进行分析。

    火车转弯时做网周运动，它具有向心加速度。火车的向心加速度是怎么产生的呢？原来，火车的车轮上有突出的轮缘（图2），如果铁路弯道的内外轨一样高，外侧车轮的轮缘就要挤压外轨内侧，使外轨发生弹性形变，外轨对轮缘的弹力就是火车转弯的向心力，如图3。但是，火车质量太大，使得火车转弯时所需要的向心力也很大，轮缘与外轨间的相互作用力太大，导致铁轨和车轮受损。如果在弯道处使外轨略高于内轨（图4），则火车转弯时铁轨对火车的支持力FN的方向不再是竖直的，而是斜向弯道内侧，它与重力G的合力指向圆心，为火车转弯提供部分向心力。这就减轻了轮缘与外轨之间的挤压。在修筑铁路时，要根据弯道实际半径和规定的行驶速度来确定内外轨的高度差，使火车转弯时所需向心力几乎完全由重力G和支持力FN的合力来提供。 一般高铁，设计时速越高，为满足列车高速运行的需要，曲线半径就应当越大。设计速度v=200 km/h= 55.6m/s时，最小曲线半径一般是R=3500 m，由mg tanθ=mv2/R求得铁道的倾角θ的正切值tanθ=v2/gR= 0.09，θ约为5.15°，标准轨道间距为1435mm，轨道内外高度差约0.1292m，倾斜并不显著，乘坐时对于弯道处外高内低的感觉也不强烈，不是有意注意根本感觉不到。

    高速铁路是封闭的，少有的几个道口也主要在直道上。尽管一般铁路不封闭，但是大多数学生没见过铁路的弯道。

    通过比较不难发现，自行车转弯与火车转弯相比，白行车转弯是更贴近学生生活的“网周运动”。

    二、拱形桥与过山车

    1.拱形桥

    汽车在经过公路上拱形桥（图5）时的运动可以看作网周运动。质量为m的汽车在拱形桥上以速度v前进，设桥面最高点处的网弧半径为R，下面分析汽车经过最高点时对桥的压力。

    以汽车为研究对象，分析汽车在拱桥最高点受到的力（图6），重力G和桥的支持力FN的合力提供汽车做网周运动的向心力F。有G- FN=mv2/R，得FN=G-mv2/R。由牛顿第三定律知，汽车对桥的压力大小为F'N=G -mv2/R。

    现实生活中，汽车运动到拱形桥最高点时，对桥面的压力小了多少呢？显著吗？

    本地有一座较陡的大桥，桥面中间弧形部分视为网周的一部分，长50m，高0.5m，由此求得其半径约625m，该桥限速40km/h（约II m/s），由上面的分析，可以求得汽车以上述速度运动到桥面最高点时的压力F'N=m（g- v2/R）=m（9.8-0.194），这与汽车在平地上运动时对地面的压力mg相差很小。

    2.过山车

    沪科版教科书列举了以下案例。

    案例：过山车（图7）能经过网形轨道顶部，车与人却不会掉下来，为什么呢？

    分析：為了更好地分析这个问题，我们先来做一个实验：如图8所示，让一个小球从倾斜轨道的不同高度处滚下，观察小球通过网形轨道时的运动情况。

    通过实验不难看出，如果小球从倾斜轨道滚下的起始高度较小，它到达网轨道底部时速度太小，就会在网形轨道的某处脱离轨道，只有当小球的速度足够大时，才能安全通过网形轨道的顶端。

    假设过山车和坐在其中的人的总质量是m，轨道半径是R，车经过顶部时的速度是v值。由向心力公式F=mv2/R可知，在轨道的顶端，过山车的速度v顶越大，人和车所需的向心力F也越大。

    当过山车沿网周运动到轨道顶端时，人与车作为一个整体，所受到的向心力是重力mg跟轨道对车的弹力FN的合力，方向向下。因为重力mg总是存在的，那么，轨道对车的弹力FN多大时，车和人才不至于掉下来呢？

    当FN=0时，过山车通过网形轨道顶端时的速度，称为临界速度v临界。

    当过山车通过网形轨道顶端时的速度恰为v临界时，重力mg恰好等于过山车做网周运动所需要的向心力，即mg= mv2/R，即 。这时，重力的作用只改变过山车的运动方向，车不会脱离轨道。

    如果过山车通过轨道顶部的速度小于v临界，所需的向心力小于车所受的重力，过山车有向下脱离轨道的趋势。

    如果过山车通过轨道顶部的速度大于v临界，所需的向心力大于车所受的重力，其不足部分将由轨道对车的弹力供给，所以这时轨道对车的弹力不为零。车子不会掉下来。

    对比汽车过拱桥和过山车，过山车应该更能让学生体会到物理知识在生活中的应用，更能激发学生的学习热情。

    既然是“生活中的圆周运动”，若能选用贴近学生生活的实例，则学生的感受会更强烈，更能激发学生的学习热情，更能加深学生对知识的理解。

    [参考文献]

    [1]人民教育出版社，课程教材研究所，物理课程教材研究开发中心.普通高中课程标准实验教科书·物理（必修2）[M].3版.北京：人民教育出版社，2010.

    [2]束炳如，何润伟.普通高中课程标准实验教科书·物理（共同必修2）[M].上海：上海科技教育出版社，2007.

    （责任编辑 南宾）