基于ANSYS的汽油机曲轴结构分析

    杨佳敏　李瑞雪

    

    

    

    摘 要：分析四缸汽油机曲轴的静态与动态性能，以支持曲轴设计的强度计算，为汽油机的曲轴优化进一步提供理论支持。首先，在用UG软件对曲轴建成三维模型的基础上，利用ANSYS网格划分，设定边界条件，采用有限元法进行静态分析。接着，讨论曲轴的形变特征和应力状态分布，根据云图结果发现曲轴应力最大值位于第三主轴颈与曲柄相连的过渡圆角处。然后，对曲轴前阶自由振动模态进行模态分析并计算，其中的模态频率旨在预测汽油机各部件间动态干扰程度，避开容易发生共振的频率。经过模态分析，发现以下三段对曲轴的正常工作影响程度依次减弱：中频段振动、高频段振动、低频段振动。实际上，低频段振动已经对曲轴工作性能没影响。

    关键词：汽油机;曲轴;有限元法;静力分析;模态分析

    中图分类号：U464文献标识码：A

    doi：10.14031/j.cnki.njwx.2019.10.006

    0 引言

    曲轴是发动机主要部件之一，在很大程度上影响到发动机的运行。作为发动机的核心，曲轴连杆、活塞等部件，支持了发动机的运作[1]。在发动机中，曲轴不仅仅要承受汽缸内的高压的急速推进，还要随着汽缸在做功的过程中发生旋转以及伴随而来的扭转力量等等。因此，在这些极端的条件下，当曲轴出现裂纹、变形或者高度磨损甚至断裂，就可能会导致整个发动机的损毁乃至报废。所以如何研制适合不同发动机、不同条件下的曲轴是非常有必要的，也是发动机向前发展的不二选择。现今，国内外采用单拐、1/2或1/4曲拐模型进行曲轴有限元分析较多[2]，往往假定相对于曲拐平面的曲轴形状和载荷对称分布。虽然这种方式计算量小，但是不能够反映出整体曲轴内部应力场的分布状态。付泽民等[3]利用曲轴的对称性选取1/4结构模型，将曲轴简化为简支梁，分析每一连杆轴颈的受力情况，但是缺少主轴颈的相应受力，计算的结果与实际工作条件下偏差较大。为了曲轴内部的应力状况表现更准确，也为了能够更准确的有限元计算，本文选取曲轴三维整体模型。

    1 曲轴三维模型建立

    在曲轴强度分析过程中，主要关注曲柄销圆角处的应力集中[4]。同时，为避免之后有限元建模过程中网格太过密集，应减少模型的单元数量和后处理求解时间。由此，在忽略曲轴油孔、倒角和圆角的前提下，得到如图1所示的三维模型，相关建模参数如表1所示。

    2 曲轴有限元模型建立

    2.1 定义材料类型

    汽油机常用曲轴材料为45号碳素钢，在ANSYS前处理中定义单元类型为8节点六面体单元solid 45，材料弹性模量3e+7，泊松比为0.3，密度为7.85 g/cm3。

    2.2 划分网格

    设置单元长度为3 mm，得到图2所示97 405节点、481 548单元的有限元模型。

    3 静力分析

    3.1 添加约束

    根据实际工作环境，从x、y、z方向对主轴颈两端完全约束，从x、y方向对中间各段主轴颈约束，约束后模型如图3所示。

    3.2 施加载荷

    在实际工作中，主要作用在曲轴上的是由燃料和空气混合物燃烧时推动活塞运动产生的作用力[5]。忽略扭矩对曲轴的作用，只考虑弯矩作用。做功汽缸的活塞运动至上止点时，连杆轴颈载荷达到最大，设其为PⅠ，计算得出转过π、2π、3π的载荷值见表2。四缸发动机的单缸做功顺序为1→3→4→2，在做功时1和4、3和2分别受力状况相同[6]。比较各缸燃气压力爆发时应力分布状况可得：3缸对应的应力值最大，1缸次之，2缸和4缸较小。本文以第3缸做功时曲轴的受力情况为研究对象，此时载荷分布如图4所示。

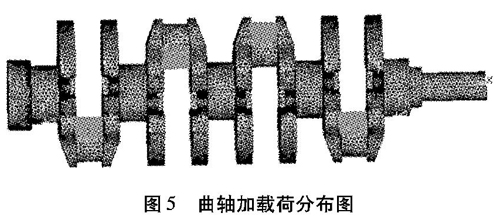
    曲轴有限元模型施加载荷后如图5所示。

    3.3 求解及后处理

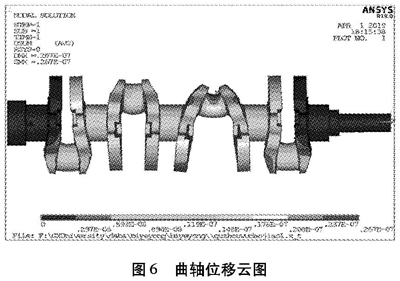
    求解完成后，调出图6所示的曲轴位移矢量云图，图7为应力分布图。

    3.4 结果分析

    由图6曲轴位移云图可知，位移变形量从蓝色到红色逐渐增大，最大位移处为第三缸连杆轴颈载荷处，形变量为0.026 7 mm。如图7所示，曲轴连杆轴颈所受应力分布由中间向两侧逐渐递增，曲轴最大应力在第三主轴颈的曲柄销处，且最大应力值为38.208 5 MPa，根据图8（c）所示，在最大应力位置相对的曲柄销处，应力值为29.717 7 MPa，因此，在曲柄销应力集中明显，易发生断裂破坏。与Setyamartana Parman[6]所得结论一致。

    4 模态分析

    模态指在模态向量和固有频率的共同作用下对机械结构产生的影响，每一阶模态对应各自的模态向量、固有频率，因而，根据模态分析是分析机构振动特性，防止与机架发生共振的重要依据。

    4.1 有限元模态分析理论

    通过有限元法将弹性体划分为有限个共节点单元，根据振动理论中多自由度系统受迫振动方程

    Mx¨+C+Kx=F（t）（1）

    式中 M、C、K—质量矩阵、阻尼矩阵、刚度矩阵;

    x¨、、x—加速度、速度、位移;

    F（t）—外加激振动。

    由于在求解固有频率和振型中，不记阻尼。振动微分方程为

    MU¨+KU=F（2）

    式中 M、K—系统质量矩阵、系统刚度矩阵;

    U—系统广义坐标矩阵;

    U¨—系统广义坐标矩阵的二阶导;

    F—广义力矩阵。

    特征方程为

    （-ω2M+K）U=0（3）

    式中 ω—系統固有频率。

    求解以上特征方程，进而得到n阶固有频率。其中，每一固有频率所对应的特征向量即为各自的振型[6，7]。

    4.2 ANSYS模态分析

    定义单元类型为solid 45，材料弹性模量为3e+7，泊松比为0.3，密度为7.8e-9，设置网格大小为5 mm，所得限元模型共有216 552个单元。

    通过Block Lanczos型自由模态分析法，提取出6阶模态。进一步求解成功后，在后处理中查看每一阶的结果云图，为图9所示。

    4.3 模态结果分析

    曲轴第2阶模态频率为237.6 Hz，与发动机工作的频率范围（26.7～134 Hz）相差较远，不会产生共振。由图9可知，曲轴第一阶振动不明显;第二阶振型来自x方向，为一阶弯曲振动;第三阶振型为z方向，为一阶弯曲振动;第四阶振型是来自y方向，为二阶弯曲振动;第五阶振型是来自x方向，为扭转振动;第六阶振型则为耦合振动，由弯曲和扭转叠加。较大的变形位于曲轴两端，应在曲轴的两端选用刚度和强度较大的轴承材料来减小发生危险的几率;且主轴颈、连杆轴颈与曲柄销连接处受力较为集中，变形量较大，易出现疲劳损伤。因此，在曲轴参数设计时可采用空心轴颈提高曲轴的稳定性。

    5 结论

    以四缸汽油机曲轴为研究对象，通过UG建立曲轴模型，在此基础上，应用ANSYS对曲轴进行静力分析和模态分析。

    在静力分析过程中可得，第三缸点火时，最大位移为第三缸连杆轴颈载荷处，形变量为0.026 7 mm。曲轴最大应力在第三主轴颈的曲柄销处，且最大应力值为38.208 5 MPa。以上数据可作为汽油机曲轴后续设计和优化的理论依据。

    在模态分析过程中可得，约束模态分析更加符合曲轴的实际工作状况。汽油机产生的振动里，中频段振动会最大程度上影响曲轴的正常工作，其次是高频段振动，低频段振动对曲轴工作性能没有影响。

    参考文献：

    [1]郭建强. 粗加工曲轴相位专用测量工具的设计与应用[J]. 柴油机设计与制造，2011， 17（4）： 43-46.

    [2]王受路. 基于ANSYS的曲轴强度有限元分析[D].济南：山东大学，2011.

    [3]付泽民，李延平，常勇，等. ANSYS环境中柴油机曲轴静动特性的有限元分析[J]. 柴油机，2006（1）： 34-38.

    [4]周志鸿. 基于ANSYS的曲柄压力机曲轴刚度分析[J]. 锻压技术，2007.

    [5]Setyamartana Parman B A A J. Finite Element Analysis of a Four-Cylinder Four Stroke Gasoline Engine Crankshaft[J]. MATEC Web of Conferences，2014.

    [6]江冰，何勇靈. 发动机曲轴应力影响因素的有限元分析[J]. 洛阳工学院学报，2002（2）： 46-50.

    [7]徐兆华，崔志琴，张腾. 基于ANSYS的6300柴油机曲轴的模态分析[J]. 煤矿机械，2012， 33（2）： 102-103.

    （05）