线段最值问题解题策略探讨

    王磊

    

    

    

    [摘要]線段最值问题是平面几何中常见的问题。该类问题一般以动点为出发点，存在众多变化量，如线段长、几何周长和面积等。求解的关键是确定最值情形，实现动态问题的具体化。

    [关键词]线段;最值;策略

    [中图分类号]G633.6[文献标识码]A [文章编号]1674-6058（2020）08-0022-02

    求线段最值是动态几何的典型问题。由于问题中给定的几何条件是变化的，存在一些特殊的动点，从而造成相关的线段长不确定。下面探讨线段最值问题的解题策略。

    策略一：直接利用垂线段最短的性质

    连接直线外一点与直线上各点的所有线段中，垂线段最短，这是垂线段的核心性质。因此涉及直线外一点与直线上点的连线问题时，可以结合垂线段的性质来直接构建模型，将动态问题转化为具体的常规问题。

    分析：本题是关于双动点的线段和问题，基本解题思路是通过适度变换将其转化为单线段问题，然后结合相应的定理来确定最值情形。对于本题，由于点

    策略二：利用两点之间线段最短公理

    “两点之间，线段最短。”在解析关于两点之间的线段最值问题时，可以结合问题情形利用上述公理来加以突破。对于不在同一直线上的多线段问题，则可以适度结合轴对称变换的方法来灵活转化。

    分析：本题求BP的长，实际上就是求PE+PF取得最小值时点P的位置。因此需要分析取得最小值时的具体情形。对于"PE+PF”，其中点P是BC上的动点，而定点E和F均位于BC的同一侧，可以通过轴对称变换的方式，将两定点转移到异侧，后续利用公理“两点之间，线段最短”来确定点P的位置。

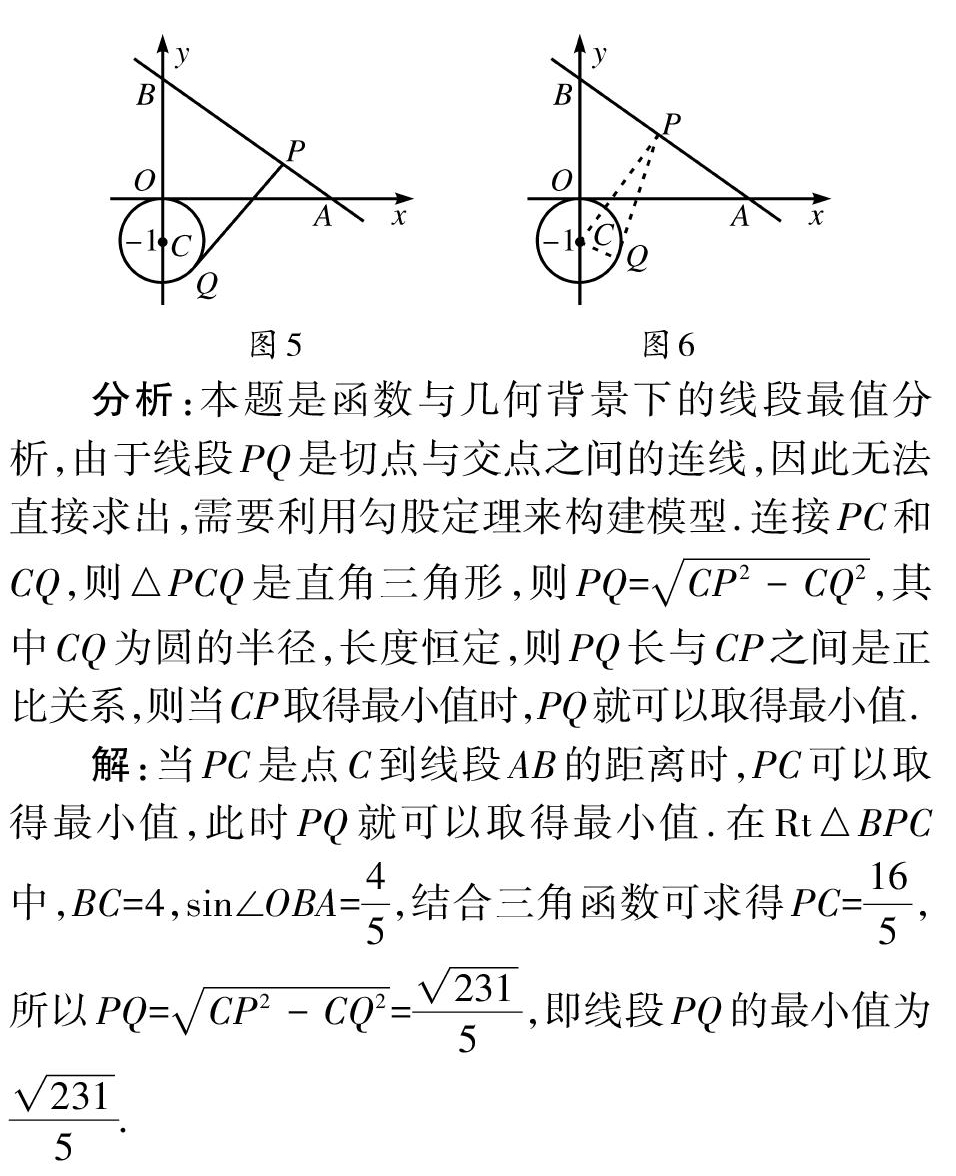
    策略三：利用函数性质分析最值

    函数思想同样可以用于线段最值问题的分析，即构建关于线段长的代数模型，利用函数性质来加以分析。比如利用二次函数来直接求最值，利用一次函数来分析数值变化。而构建函数时需要结合公式定理，常用的有勾股定理、相似三角形的边长比例特性。

    策略四：通过“画圆”确定取值情形

    绘制轨迹圆是求解动点问题的方式之一，在分析动点背景下的线段最值问题时，可以通过“画圆”来确定动点的运动轨迹，进而结合相关性质定理确定线段的最值。

    分析：根据题干条件可知DF=DB=CD始终成立，随着点E的变化点F的位置也会变化，但DF始终与DB等长，则点F的轨迹就为一个圆，则可以通过“画圆”来构建点F的轨迹，进而确定AF的最值。