谈课堂教学中数学核心素养的提升
【摘要】新一轮的数学课程改革提出六大核心素养:数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析.如何将提升学生的核心素养落实到位,是当前中学教师亟需解决的问题.六大核心素养是在比较各国课程标准,研究国际数学教育发展,结合我国基础教育的状况下提出的,既继承了上一轮课程改革的优秀成果,又推动了我国数学教育的国际化.课堂教学将数学核心素养落实到位,学生才能理解数学.
【关键词】核心素养;直观想象;截面;球
笔者在市教学研讨会上执教了一节高三理科复习课《球与几何体的切接问题》,在备课的过程中深入思考教学中如何落实数学核心素养,提升学生对问题的理解和解决能力.立体几何教学侧重提升学生的直观想象素养,备课中以高考真题为切入点,以数学方法为立足点,以提升数学核心素养为落脚点.
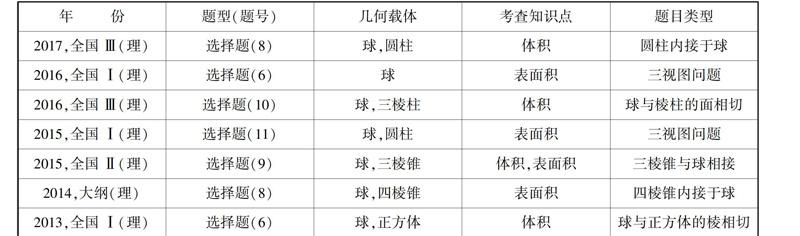
1分析高考真题,提炼关键信息年份题型(题号) 几何载体考查知识点题目类型2017,全国Ⅲ(理)选择题(8)球,圆柱体积圆柱内接于球2016,全国Ⅰ(理)选择题(6)球表面积三视图问题2016,全国Ⅲ(理)选择题(10)球,三棱柱体积球与棱柱的面相切2015,全国Ⅰ(理)选择题(11)球,圆柱表面积三视图问题2015,全国Ⅱ(理)选择题(9)球,三棱锥体积,表面积三棱锥与球相接2014,大纲(理)选择题(8)球,四棱锥表面积四棱锥内接于球2013,全国Ⅰ(理)选择题(6)球,正方体体积球与正方体的棱相切分析(1)真题中与球相关的题目侧重考查学生的空间想象能力,对作图能力要求较高.表现在:五年高考7题中3题有图,其中2题为三视图问题.说明高考题目要求学生必须能够作出直观图,然后利用直观图分析问题,学生要有较强的几何作图能力;(2)以截面问题为主,需选择恰当的截面解决问题,考查平面化的方法;(3)几何载体多变,以体积或表面积的计算为主.
结论高考题目从“几何作图”和“分析图形”两个角度考查直观想象核心素养,同时考查“逻辑推理”和“数学运算”两个核心素养.
2选择典型例题,提炼数学方法
鉴于对高考真题的分析,例题的选择具备以下两点特征:(1)题目中通常无直观图;(2)能从多角度入手解决问题.
例1球O与棱长为2的正方体ABCD-A1B1C1D1的各个面都相切,点M为棱DD1的中点,则平面ACM截球O所得截面的面积为().
A.4π3B. πC. 2π3D. π3
教学片段1:
师:同学们,你们解答这道题的困惑在哪里?
生(齐答):不知道截面的位置.
师:截面的形状是什么?
生(齐答):圆.
小组合作交流:大家思考截面的准确位置在哪里?(教师展示直观图)
生1:截面的形状是圆,在O1点处与直线AC相切.
师:如何求出这个截面圆的半径?请小组讨论一下.
生2:在截面O1DMO中,△O1OM为直角三角形,求出OO2的长度,然后利用勾股定理得出半径O1O2的长度.
生3:在Rt△O1OM中,利用射影定理求.由OO12= O1O2×O1M得出半径O1O2的长度.
生4:以O为坐标原点,OM为x轴,OO1为y轴,建立平面直角坐标系.求出直线O1M和直线OO2的方程,联立这两条直线的方程得到O2的坐标,然后利用两点间的距离公式得出半径O1O2的长度.
师:很好!咱们同学利用解析法解决立体几何问题,知识交汇,思路可嘉!请同学们思考,解决此类问题的关键是什么?
生5:首先,画出直观图,选取合适的截面图;然后,利用平面几何知识解答.
师:点M的位置与所画直观图正方体顶点字母顺序的关联程度很强,如果大家发现不容易看出截面图时,就要重新画图,交换点M的位置.按照“画出直观图——寻找截面图——确定算法”三步走,此种类型的题目可快速解答!
设计意图让学生有意识地去寻找截面图,认识球体中重要的三角形——球的半径、球心到小圆面的距离、小圆的半径构成的直角三角形.体会勾股定理和射影定理在解决此类问题中的应用.使学生对高考题形成初步感知,掌握问题求解的一般思路,重点强化平面化方法.
巩固反馈棱长为1的正方体ABCD-A1B1C1D1的8个顶点都在球O的表面上,E,F分别是棱AA1,DD1的中点,则直线EF被球O截得的线段长为().
A.22B.1C.1+22D.2
设计意图强化学生在球中寻找截面和构造重要直角三角形的意识,进一步明确“构造直角三角形”是解决此类问题的基本方法.
例2(2009全國Ⅰ理15)直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于().
教学片段2:
师:请同学们作出直观图,寻找截面,并确定算法.
2分钟后.
师:你解答此题的困惑在哪里?
生6:球心和截面小圆的半径找不到.
师:换个角度想,直棱柱的外接球的球心位置在哪个平面内?
生7:(讨论后)球心在直棱柱高线的中垂面处.但是,具体的位置不好确定.
师:具体的说,直棱柱的外接球的球心在上、下底面外接圆圆心连线的中点处.
师:那么,球心到小圆面的距离是否可以直接得出?
生7:距离为1.就是直棱柱侧棱长的一半.
生(齐):哦……
师:我们已经构造了直角三角形,请同学们思考,如何求出△ABC外接圆的半径?
生8:利用正弦定理求出.
设计意图几何体的结构特征可以为解题提供思路.基于直棱柱和球的结构特征,本例中球心的位置可以“忽略”,球心到小圆面的距离就是直棱柱侧棱长的一半,小圆的半径就是底面三角形外接圆的半径,用勾股定理求得直棱柱的外接球半径即可.熟练之后,此类问题便可以“以想代算”.同时,本例与正弦定理关联,拓宽了解题视野.
巩固反馈已知三棱锥P-ABC,在底面△ABC中,∠CAB=60°,BC=3,PA⊥面ABC,PA=2,则此三棱锥外接球的半径为().
设计意图本题的几何体可以补体为直棱柱,然后采用例2的方法,快速找到球心到小圆面的距离,简化运算.让学生在解题的过程中体会补形的思想与类比的方法,提倡并鼓励一题多解.
3开展头脑风暴,优化思维结构
例3四面体ABCD中,共顶点A的三条棱两两相互垂直,且其长别分为1、6、3,若四面体ABCD的四个项点同在一个球面上,则这个球的表面积为().
师:同学们思考,如何得到四面体ABCD外接球的半径?
生9:因为四面体ABCD中,共顶点A的三条棱两两相互垂直,可以构造长方体,从而得出外接球的直径为2R=12+(6)2+32=4.
师:非常好!请同学们思考,哪种类型的四面体外接球问题可以构造长方体?
生10:共顶点的三条侧棱两两垂直.
生11:共顶点的三个面互相垂直.
生12:底面为直角三角形,并且有一条侧棱垂直于底面.
师:很好,还有吗?
生(齐):(沉默)没有了.
师:(在长方体中板演)三条棱顺次首尾相连,且互相垂直,能否构造长方体?
生(齐):……可以.
师:(在长方体中板演)三组相对棱长度分别相等的四面体,能否构造长方体?
生(齐):……可以.
师:其实,只要是从长方体中提取不共面的四个点构成的四面体,都可以进行如此“逆”操作,补体为一个长方体.
师:请同学们对上述问题进行归纳研究,并分析此四面体的体积与补体得到的长方体的体积之间的关系?留作课后研究性学习,写成小论文,展示交流.
设计意图通过构造几何体得到问题的答案,本质是“建立数学模型”和“解答数学模型”的过程,提升了学生的几何直观素养和数学建模素养.留给学生1个问题,让学生进行研究性学习,提升认真钻研的科学精神.
巩固反馈(快速抢答)已知正四面体的棱长为2a,求这个正四面体外接球的半径.
设计意图将构造长方体的问题迁移到构造正方体的问题之中,平淡出奇,凸显“模型化”方法的解题魅力.
4几点思考
4.1课堂教学要“以人为本”提升核心素养.
“以人为本”就是以促进人的发展为本,注重学生数学思维品质的发展和数学应用能力的提升.教会学生学会分析问题和解决问题特别重要,但是学生能够思维发散,创造性地提出新的问题,更加符合新时期“创新型”人才培养的格局.立体几何教学,学生的空间想象力的提升是第一任务,学生学会分析立体图形,能主动构造和使用几何模型解题,几何直观素养才算得到提升.
4.2课堂教学要将“知识学习”与“素养提升”并重.
学生的数学核心素养是可发展、可提升的.教师备课中例习题的选择要尽量入口宽泛,讲解时体现数学思想方法.如立体几何的教学,教师授课时注重多采用“举例”、“建模”、“类比”等方式对知识整合,提升空间想象能力.同时,“补体法”、“分割法”、“等体积法”、“平面化方法”、添加各种辅助线(或辅助平面)等都屬于立体几何中的算法问题,是立体几何教学中要提升的“数学运算”素养.
4.3课堂教学的一个重要任务是“数学育人”.
数学教学既要教会学生数学知识,还要教会学生用数学知识解决生活中的问题.即用数学的眼光看问题,用数学的理性思维分析问题,用数学的方法去解决问题.数学推理的严谨性影响人的一生,对树立求真务实的价值观非常有利.学生学习了有用的数学、能用的数学和会用的数学,数学教育的核心价值才能够得到体现.
作者简介崔文(1979—),男,中学数学一级教师,威海市教学能手,威海市教育名家工作室成员.主要从事中学数学课堂教学研究,在《中学数学杂志》、《中国数学教育》、《数理天地》等期刊发表论文10余篇.
【关键词】核心素养;直观想象;截面;球
笔者在市教学研讨会上执教了一节高三理科复习课《球与几何体的切接问题》,在备课的过程中深入思考教学中如何落实数学核心素养,提升学生对问题的理解和解决能力.立体几何教学侧重提升学生的直观想象素养,备课中以高考真题为切入点,以数学方法为立足点,以提升数学核心素养为落脚点.
1分析高考真题,提炼关键信息年份题型(题号) 几何载体考查知识点题目类型2017,全国Ⅲ(理)选择题(8)球,圆柱体积圆柱内接于球2016,全国Ⅰ(理)选择题(6)球表面积三视图问题2016,全国Ⅲ(理)选择题(10)球,三棱柱体积球与棱柱的面相切2015,全国Ⅰ(理)选择题(11)球,圆柱表面积三视图问题2015,全国Ⅱ(理)选择题(9)球,三棱锥体积,表面积三棱锥与球相接2014,大纲(理)选择题(8)球,四棱锥表面积四棱锥内接于球2013,全国Ⅰ(理)选择题(6)球,正方体体积球与正方体的棱相切分析(1)真题中与球相关的题目侧重考查学生的空间想象能力,对作图能力要求较高.表现在:五年高考7题中3题有图,其中2题为三视图问题.说明高考题目要求学生必须能够作出直观图,然后利用直观图分析问题,学生要有较强的几何作图能力;(2)以截面问题为主,需选择恰当的截面解决问题,考查平面化的方法;(3)几何载体多变,以体积或表面积的计算为主.
结论高考题目从“几何作图”和“分析图形”两个角度考查直观想象核心素养,同时考查“逻辑推理”和“数学运算”两个核心素养.
2选择典型例题,提炼数学方法
鉴于对高考真题的分析,例题的选择具备以下两点特征:(1)题目中通常无直观图;(2)能从多角度入手解决问题.
例1球O与棱长为2的正方体ABCD-A1B1C1D1的各个面都相切,点M为棱DD1的中点,则平面ACM截球O所得截面的面积为().
A.4π3B. πC. 2π3D. π3
教学片段1:
师:同学们,你们解答这道题的困惑在哪里?
生(齐答):不知道截面的位置.
师:截面的形状是什么?
生(齐答):圆.
小组合作交流:大家思考截面的准确位置在哪里?(教师展示直观图)

生1:截面的形状是圆,在O1点处与直线AC相切.
师:如何求出这个截面圆的半径?请小组讨论一下.
生2:在截面O1DMO中,△O1OM为直角三角形,求出OO2的长度,然后利用勾股定理得出半径O1O2的长度.
生3:在Rt△O1OM中,利用射影定理求.由OO12= O1O2×O1M得出半径O1O2的长度.
生4:以O为坐标原点,OM为x轴,OO1为y轴,建立平面直角坐标系.求出直线O1M和直线OO2的方程,联立这两条直线的方程得到O2的坐标,然后利用两点间的距离公式得出半径O1O2的长度.
师:很好!咱们同学利用解析法解决立体几何问题,知识交汇,思路可嘉!请同学们思考,解决此类问题的关键是什么?
生5:首先,画出直观图,选取合适的截面图;然后,利用平面几何知识解答.
师:点M的位置与所画直观图正方体顶点字母顺序的关联程度很强,如果大家发现不容易看出截面图时,就要重新画图,交换点M的位置.按照“画出直观图——寻找截面图——确定算法”三步走,此种类型的题目可快速解答!
设计意图让学生有意识地去寻找截面图,认识球体中重要的三角形——球的半径、球心到小圆面的距离、小圆的半径构成的直角三角形.体会勾股定理和射影定理在解决此类问题中的应用.使学生对高考题形成初步感知,掌握问题求解的一般思路,重点强化平面化方法.
巩固反馈棱长为1的正方体ABCD-A1B1C1D1的8个顶点都在球O的表面上,E,F分别是棱AA1,DD1的中点,则直线EF被球O截得的线段长为().
A.22B.1C.1+22D.2
设计意图强化学生在球中寻找截面和构造重要直角三角形的意识,进一步明确“构造直角三角形”是解决此类问题的基本方法.
例2(2009全國Ⅰ理15)直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于().
教学片段2:
师:请同学们作出直观图,寻找截面,并确定算法.
2分钟后.
师:你解答此题的困惑在哪里?
生6:球心和截面小圆的半径找不到.
师:换个角度想,直棱柱的外接球的球心位置在哪个平面内?
生7:(讨论后)球心在直棱柱高线的中垂面处.但是,具体的位置不好确定.
师:具体的说,直棱柱的外接球的球心在上、下底面外接圆圆心连线的中点处.
师:那么,球心到小圆面的距离是否可以直接得出?
生7:距离为1.就是直棱柱侧棱长的一半.
生(齐):哦……
师:我们已经构造了直角三角形,请同学们思考,如何求出△ABC外接圆的半径?
生8:利用正弦定理求出.
设计意图几何体的结构特征可以为解题提供思路.基于直棱柱和球的结构特征,本例中球心的位置可以“忽略”,球心到小圆面的距离就是直棱柱侧棱长的一半,小圆的半径就是底面三角形外接圆的半径,用勾股定理求得直棱柱的外接球半径即可.熟练之后,此类问题便可以“以想代算”.同时,本例与正弦定理关联,拓宽了解题视野.
巩固反馈已知三棱锥P-ABC,在底面△ABC中,∠CAB=60°,BC=3,PA⊥面ABC,PA=2,则此三棱锥外接球的半径为().
设计意图本题的几何体可以补体为直棱柱,然后采用例2的方法,快速找到球心到小圆面的距离,简化运算.让学生在解题的过程中体会补形的思想与类比的方法,提倡并鼓励一题多解.
3开展头脑风暴,优化思维结构
例3四面体ABCD中,共顶点A的三条棱两两相互垂直,且其长别分为1、6、3,若四面体ABCD的四个项点同在一个球面上,则这个球的表面积为().
师:同学们思考,如何得到四面体ABCD外接球的半径?
生9:因为四面体ABCD中,共顶点A的三条棱两两相互垂直,可以构造长方体,从而得出外接球的直径为2R=12+(6)2+32=4.
师:非常好!请同学们思考,哪种类型的四面体外接球问题可以构造长方体?
生10:共顶点的三条侧棱两两垂直.
生11:共顶点的三个面互相垂直.
生12:底面为直角三角形,并且有一条侧棱垂直于底面.
师:很好,还有吗?
生(齐):(沉默)没有了.
师:(在长方体中板演)三条棱顺次首尾相连,且互相垂直,能否构造长方体?
生(齐):……可以.
师:(在长方体中板演)三组相对棱长度分别相等的四面体,能否构造长方体?
生(齐):……可以.
师:其实,只要是从长方体中提取不共面的四个点构成的四面体,都可以进行如此“逆”操作,补体为一个长方体.
师:请同学们对上述问题进行归纳研究,并分析此四面体的体积与补体得到的长方体的体积之间的关系?留作课后研究性学习,写成小论文,展示交流.
设计意图通过构造几何体得到问题的答案,本质是“建立数学模型”和“解答数学模型”的过程,提升了学生的几何直观素养和数学建模素养.留给学生1个问题,让学生进行研究性学习,提升认真钻研的科学精神.
巩固反馈(快速抢答)已知正四面体的棱长为2a,求这个正四面体外接球的半径.
设计意图将构造长方体的问题迁移到构造正方体的问题之中,平淡出奇,凸显“模型化”方法的解题魅力.
4几点思考
4.1课堂教学要“以人为本”提升核心素养.
“以人为本”就是以促进人的发展为本,注重学生数学思维品质的发展和数学应用能力的提升.教会学生学会分析问题和解决问题特别重要,但是学生能够思维发散,创造性地提出新的问题,更加符合新时期“创新型”人才培养的格局.立体几何教学,学生的空间想象力的提升是第一任务,学生学会分析立体图形,能主动构造和使用几何模型解题,几何直观素养才算得到提升.
4.2课堂教学要将“知识学习”与“素养提升”并重.
学生的数学核心素养是可发展、可提升的.教师备课中例习题的选择要尽量入口宽泛,讲解时体现数学思想方法.如立体几何的教学,教师授课时注重多采用“举例”、“建模”、“类比”等方式对知识整合,提升空间想象能力.同时,“补体法”、“分割法”、“等体积法”、“平面化方法”、添加各种辅助线(或辅助平面)等都屬于立体几何中的算法问题,是立体几何教学中要提升的“数学运算”素养.
4.3课堂教学的一个重要任务是“数学育人”.
数学教学既要教会学生数学知识,还要教会学生用数学知识解决生活中的问题.即用数学的眼光看问题,用数学的理性思维分析问题,用数学的方法去解决问题.数学推理的严谨性影响人的一生,对树立求真务实的价值观非常有利.学生学习了有用的数学、能用的数学和会用的数学,数学教育的核心价值才能够得到体现.
作者简介崔文(1979—),男,中学数学一级教师,威海市教学能手,威海市教育名家工作室成员.主要从事中学数学课堂教学研究,在《中学数学杂志》、《中国数学教育》、《数理天地》等期刊发表论文10余篇.

