折纸法在初中几何教学中的应用

     张庆大

    

    

    

    [摘要]在几何教学中应用折纸操作的教学方法，能激发学生的学习兴趣，培养学生的想象能力和实践创新能力，

    [关键词]折纸法;初中几何教学;应用

    [中图分类号]G633.6 [文献标识码]A [文章编号]1674-6058（2020）05-0012-02

    所谓“折纸法”就是在几何教学中，为激发学生学习兴趣，培养学生想象能力和实践创新能力，采用折纸方法教学。

    一、教学前期准备

    第一，通过调查，全面了解学生当前的学习情况，明确学生的学习需求，除了在课堂上给予学生更多的发言机会，做好新旧知识之间的衔接工作以外，还应当在课后加强与学生互动，以便更好地了解学生的想法，保证设计的“折纸奥秘”既能够满足教学需求，又能够充分激发学生的学习兴趣。

    第二，根据学生的实际情况将“折纸奥秘”的教学目标拆分成若干个小目标，要求学生在不同的教学阶段完成不同的教学目标，以此保证数学学习有针对性，引导学生持续学习。

    第三，根据实际教学内容准备好纸张、胶水、剪刀等工具辅助“折纸奥秘”操作顺利完成。

    二、教学目标设计

    在开展教学活动时，除了帮助学生获得更多的理论知识以外，还应当使教学内容贴近生活，保证学生能够具备应用所学知识解决实际问题，另外，教学活动以及教学任务应当是顺应学生自我的认知结构，基于上述分析，本次“折纸奥秘”的整体教学目标设置如下。

    （1）通过将折纸活动与几何教学相结合，使学生更加直观地认识几何的特性以及变化规律，增强学生的空间想象力，降低几何教学难度，提升几何教学效果。

    （2）通过动手折纸，实现学生生活中获得的直接经验和课堂中获得的间接经验的有机结合，以此有效激发学生的学习兴趣，使其积极主动参与到几何内容的学习之中，保证良好的课堂教学效率。

    （3）通过折纸活动培养学生的动手操作能力、团队协作能力和独立思考能力。

    三、教学内容设计

    在利用“折纸法”进行正多边形的学习时，主要采用理论讲解、直观演示以及学生小组讨论三种教学方法，折叠正三角形、正五边形过程中的各个数学原理为本次项目教学的重点，涉及的教具包括正方形、长方形以及三角形纸张，具体“折纸奥秘”的教学实施过程如下。

    1.旧知识的复习与回顾，新课题的思考与探讨

    （1）通过多媒体软件向学生展示螺母和不同的正多边形形状，设置问题：图中的螺母是什么形状？正多边形的各个边长长度相等吗？以此展开活动，引导学生主动思考、探索多边形的特点。

    （2）在学生回答问题之后进一步追问：图中哪些形状是正多边形？正多边形的共同点是什么？以此引导学生归纳正多边形的性质，总结正多边形的定义，使学生对正多边形有一个初步的认知，为本节课折纸活动的开展做好铺垫。

    2.动手实践，通过折纸探究新知

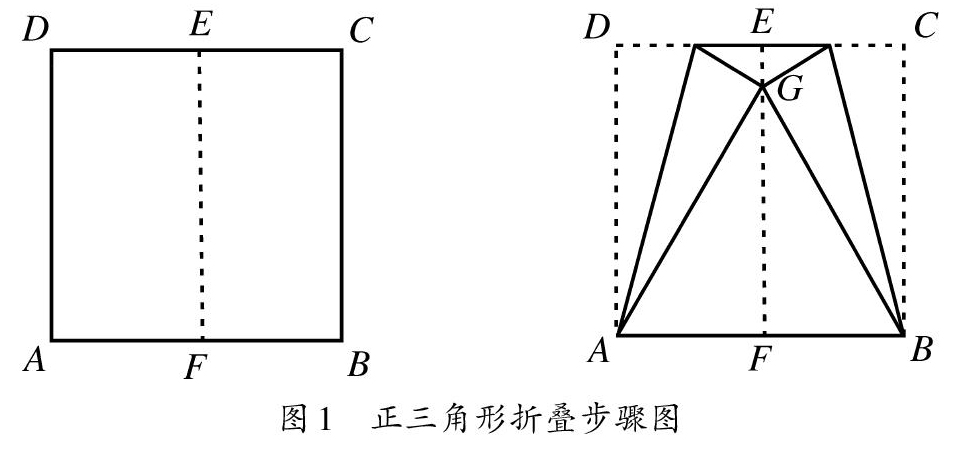
    （1）为每一位学生配发纸张，设计任务：是否能够通过折纸的方式将正方形纸张变成正三角？开展活动：教会学生正三角形的折叠方法，首先将正方形纸张AD边与BC边对折，得到折痕EF;其次，以A点为支撑，将AD边向内翻折，使D点落在折痕EF之上，得到G点，重复上述步骤，以B点为支撑，将CB边向内翻折，使c点与G点重合;最后，用剪刀沿着A、G、B裁剪，得到的三角形ABG即为正三角形（如图1和图2），折叠完成后引导学生对图形进行观察，包括三角形的边长、每个角的角度等，以加深学生对正三角形各边相等、角度相同等特性的认识，使学生明白正三角形的构造。

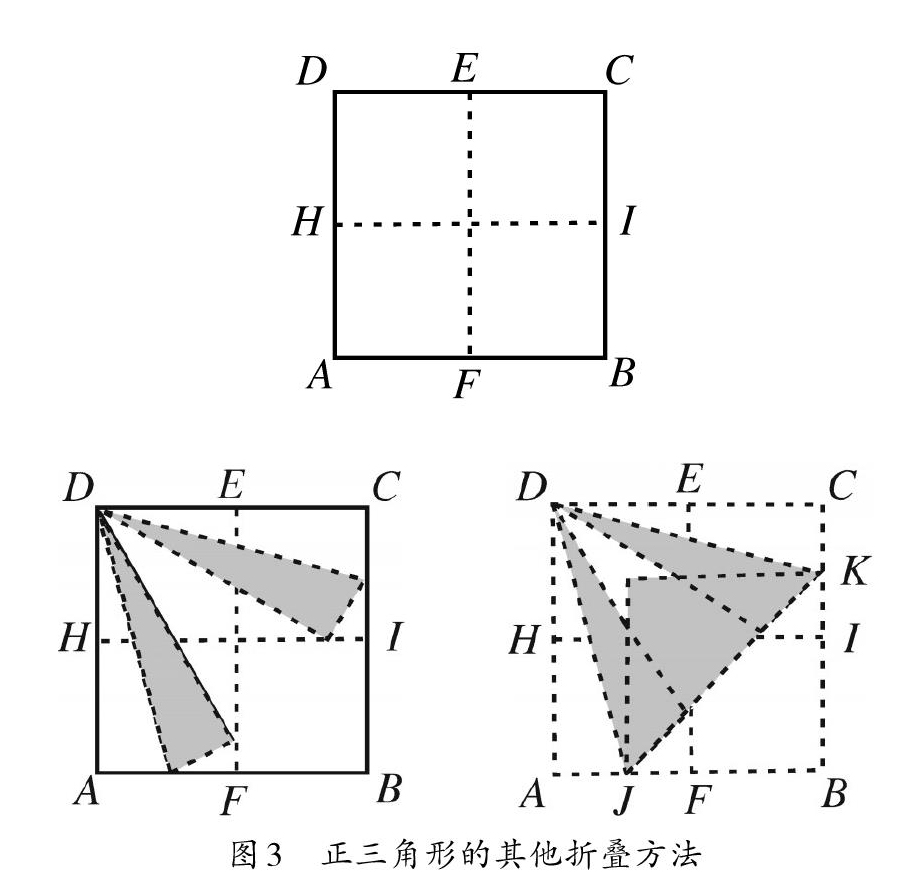
    （2）延伸问题，要求学生根据正多边形的定义对折纸的原理（当三角形的三条边与正方形的边长相等时，便可通过折叠正方形得到正三角形）进行思考，并询问学生是否能够利用其他的方法获得正三角形，另一种折叠方法：上下、左右两次对折正方形后，以D点为支撑向内翻折AD边、CD边，使A点落在EF上并形成折痕DJ，使C点落在HI上并形成折痕DK，以KJ边为支撑将三角形BJK向内翻折，得到图形DJK即为正三角形（如图3所示），折叠完成后，要求学生对两种折叠方法进行比较，使学生养成从多个不同的角度思考问题的习惯，加深学生对正三角形特征、性质的认知。

    （3）引导学生对折纸过程中涉及的几何原理“有一个角是60°的等腰三角形是等边三角形”进行思考和总结，首先要求学生对正三角形的折叠方法进行思考;其次让学生根据课本中的知识对折叠出来的三角形的各个角的角度进行判断，在这过程中，教会学生以下正三角形的折叠方法：

    上下两次对折正方形得到折痕IF，然后对折DC-丌得到折痕GH;以F点为支撑向内翻折CF边使c点落在HG上得到E点和C点，此时形成的/_EFI=60。;以E点为支点平行翻折DA边，折痕过点E得到t，点，用笔在Ⅳ边上作一点K，使KJ=JF，用笔描出EF对应的边EK，得到的三角形EKF即为正三角形，

    引导学生思考：Z～FI=60。，且EF=EK，是否满足等边三角形的判定定理？以此加深学生对等边三角形原理的认知，使学生能够通过举一反三，体现教学的灵活性，

    3.对折纸活动进行归纳，培养学生利用理论证明问题的能力

    根据折纸，要求学生将边AF记作a，AE记作b，EF记作c，然后对正方形ABCD、正方形EFGH以及正方形IJKL的面积进行观察和计算，并引导学生利用面积割补法得出勾股定理，在计算和证明的過程中，让学生积极开展小组讨论，并鼓励学生在交流之中得出不同的证明方法和计算方法，在开展小组讨论的过程中，设计以下问题：

    什么是勾股定理？利用折纸活动学习勾股定理体现了哪些数学思想与方法？在折纸活动中你有哪些收获？你有其他证明勾股定理的方法吗？

    4.布置课后作业，巩固学习效果

    （1）如何通过折纸的方式将两个大小相同的正方形合并成一个面积更大的正方形？

    （2）如何利用勾股定理折叠出一个正三角形？