探究2016年高考四川卷函数导数试题的命题方法
杨苍洲+崔红光
面对一个试题,大多数人都喜欢研究试题的解法,而笔者却更喜欢探究试题背后的故事.笔者常思考,命题者是如何得到问题,并将其设计成试题的呢?
试题的解题方法固然很值得研究,但是此类研究往往只停留于对试题较低层次的认识.而探究试题的命题背景、命题方法,不仅有助于在解题中寻找入口、理顺思路、开阔视野,从而提高解题水平,同时也能大幅提高教师的命题水平.下面笔者探究2016年高考四川卷函数与导数试题的命题方法,并根据此命题方法进行试题命制.
1试题与解答
题目(2016年高考四川卷理科)设函数f(x)=ax2-a-lnx,其中a∈R.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)确定a的所有可能取值,使f(x)>1x-e1-x在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
解析(Ⅰ)由题意,f′(x)=2ax-1x=2ax2-1x,x>0.
①当a≤0时,2ax2-1≤0,f′(x)≤0,f(x)在(0,+∞)上单调递减.
②当a>0时,
f′(x)=2ax+12ax-12ax.
当x∈0,12a时,f′(x)<0;
当x∈12a,+∞时,f′(x)>0.
故f(x)在0,12a上单调递减,在12a,+∞上单调递增.
(Ⅱ)令g(x)=1x-e1-x=ex-1-xxex-1,
令s(x)=ex-1-x,则s′(x)=ex-1-1.
而当x>1时,s′(x)>0,所以s(x)在(1,+∞)内单调递增.又由s(1)=0,有s(x)>0,
从而当x>1时,g(x)>0.
(1)当a≤0,x>1时,f(x)=ax2-a-lnx<0,此时f(x)
h′(x)=2ax-1x+1x2-e1-x>x-1x+1x2-1x=x3-2x+1x2>x2-2x+1x2>0.因此h(x)在(1,+∞)内单调递增.又由h(1)=0,从而当x>1时,有h(x)>0,即f(x)>g(x)成立.
(3)当a>0且12a>1时,由(Ⅰ)知f12a0,因此f(x)>g(x)不恒成立.
综上所述,a≥12.
2命题手法探究
上述试题是怎样命制出来的呢?
命题者构造了过定点(1,0)的函数族f(x)=ax2-a-lnx.随着实数a取值范围的变化,函数f(x)的单调性、极值都发生变化.
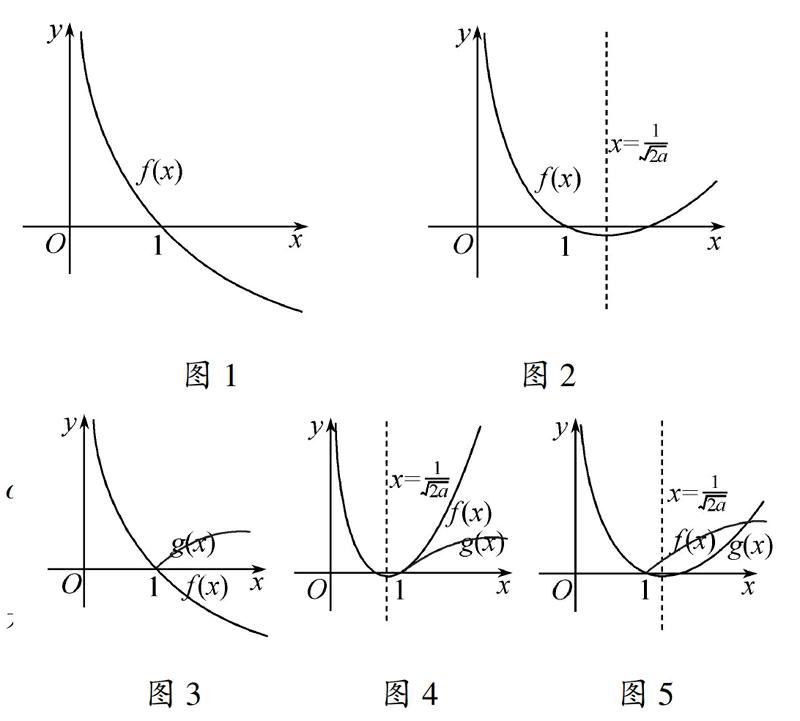
当a≤0时,函数f(x)在区间(0,+∞)单调递减(如图1);
当a>0时,函数f(x)在区间0,12a上单调递减,在区间12a,+∞上单调递增(如图2).图1图2于是命题者设置了问题(Ⅰ):讨论函数f(x)=ax2-a-lnx的单调性.
为了增加试题难度,命题者考虑引入新函数,于是构造了过点(1,0)的函数g(x)=1x-e1-x.
由于动函数f(x)与定函数g(x)相交于点(1,0).于是考虑比较f(x)与g(x)在定点两侧函数值的大小.为减小试题的难度,命题者只研究两个函数在定点右侧的情况,即研究x>1时,两函数值的大小关系.
如图3,当a≤0时,函数f(x)的图像恒在函数g(x)图像的下方.
图3图4图5如图4,当a>0且12a≤1时,函数f(x)图像恒在函数g(x)图像的上方.
如图5,当a>0且12a>1时,函数f(x),g(x)的图像有异于点(1,0)的又一交点(p,q).
当1p,函数f(x)的图像在函数g(x)图像的上方.
根据上述分析,命题者设置了问题(Ⅱ):确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.
此类问题的命题手法为:研究过同一定点的两个函数(其中一个为动函数,一个为定函数)的函数图像关系,并从中提炼设置问题.
如能探明试题的命题方法,解题者就不难得到解题思路了.讲题时,也将有利于教师讲清问题的来龙去脉.
3命制新题
基于对2016年高考四川卷理科函数导数试题命题手法的研究.模仿此命题手法,笔者尝试编制新题.
新题1:已知函数f(x)=ex-ax有极值1.
(Ⅰ)求实数a,并确定该极值为极大值还是极小值;
(Ⅱ)当x∈0,+∞)时,f(x)≥mxln(x+1)+1恒成立,求实数m的取值范围.
解(Ⅰ)f′(x)=ex-a.
①当a≤0时,f′(x)>0,f(x)在(-∞,+∞)上单调递增,无极值,不符合题意;
②当a>0时,f′(x)=0,x=lna,当x∈(-∞,lna)时,f′(x)<0,f(x)单调递减;
当x∈(lna,+∞)时,f′(x)>0,f(x)单调递增.
当x=lna时,f(x)取到极小值,f(lna)=a-alna=1,得a=1.
(Ⅱ)f(x)=ex-x.
令g(x)=ex-x-mxln(x+1)-1,x∈[0,+∞),g′(x)=ex-1-mln(x+1)-mxx+1.
构造函数h(x)=ex-1-mln(x+1)-mxx+1,x∈[0,+∞),h′(x)=ex-m1(x+1)2+1x+1,h′(0)=1-2m.
①当m≤0时,h′(x)>0,h(x)在0,+∞)上单调递增,h(x)min=0,则g′(x)>0,g(x)单调递增,g(x)min=0,
所以g(x)≥0,故ex-x≥mxln(x+1)+1恒成立.
②当00,h(x)在0,+∞)上单调递增,h(0)min=0,则g′(x)>0,g(x)单调递增,g(x)min=0,所以g(x)≥0,ex-x≥mxln(x+1)+1恒成立,此时0
新题2:已知函数f(x)=x2-x,g(x)=ex-ax-1.
(Ⅰ)讨论函数g(x)的单调性;
(Ⅱ)当x>0时,f(x)≤g(x)恒成立,求实数a的取值范围.
解(Ⅰ)g′(x)=ex-a.
①当a≤0时,g′(x)>0,g(x)在(-∞,+∞)上单调递增;②当a>0时,当x∈(-∞,lna)时,g′(x)<0,g(x)单调递减,当x∈(lna,+∞)时,g′(x)>0,g(x)单调递增.
作者简介杨苍洲(1979—),男,福建泉州人,中学一级教师,研究方向:数学教学,命题研究.泉州市中小学名师工作室成员,福建省第二届教师教学技能大赛特等奖者.多次参与泉州市质检命题,福建省质检命题,福建省高考命题.在中数期刊发表文章200多篇.
崔红光(1981—),女,福建泉州,中学一级教师,研究方向:数学教学,命题研究.曾获得泉州市说课比赛二等奖,泉州市普通高中高考九科试卷命制技能比赛二等奖.
面对一个试题,大多数人都喜欢研究试题的解法,而笔者却更喜欢探究试题背后的故事.笔者常思考,命题者是如何得到问题,并将其设计成试题的呢?
试题的解题方法固然很值得研究,但是此类研究往往只停留于对试题较低层次的认识.而探究试题的命题背景、命题方法,不仅有助于在解题中寻找入口、理顺思路、开阔视野,从而提高解题水平,同时也能大幅提高教师的命题水平.下面笔者探究2016年高考四川卷函数与导数试题的命题方法,并根据此命题方法进行试题命制.
1试题与解答
题目(2016年高考四川卷理科)设函数f(x)=ax2-a-lnx,其中a∈R.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)确定a的所有可能取值,使f(x)>1x-e1-x在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
解析(Ⅰ)由题意,f′(x)=2ax-1x=2ax2-1x,x>0.
①当a≤0时,2ax2-1≤0,f′(x)≤0,f(x)在(0,+∞)上单调递减.
②当a>0时,
f′(x)=2ax+12ax-12ax.
当x∈0,12a时,f′(x)<0;
当x∈12a,+∞时,f′(x)>0.
故f(x)在0,12a上单调递减,在12a,+∞上单调递增.
(Ⅱ)令g(x)=1x-e1-x=ex-1-xxex-1,

令s(x)=ex-1-x,则s′(x)=ex-1-1.
而当x>1时,s′(x)>0,所以s(x)在(1,+∞)内单调递增.又由s(1)=0,有s(x)>0,
从而当x>1时,g(x)>0.
(1)当a≤0,x>1时,f(x)=ax2-a-lnx<0,此时f(x)
h′(x)=2ax-1x+1x2-e1-x>x-1x+1x2-1x=x3-2x+1x2>x2-2x+1x2>0.因此h(x)在(1,+∞)内单调递增.又由h(1)=0,从而当x>1时,有h(x)>0,即f(x)>g(x)成立.
(3)当a>0且12a>1时,由(Ⅰ)知f12a
综上所述,a≥12.
2命题手法探究
上述试题是怎样命制出来的呢?
命题者构造了过定点(1,0)的函数族f(x)=ax2-a-lnx.随着实数a取值范围的变化,函数f(x)的单调性、极值都发生变化.
当a≤0时,函数f(x)在区间(0,+∞)单调递减(如图1);
当a>0时,函数f(x)在区间0,12a上单调递减,在区间12a,+∞上单调递增(如图2).图1图2于是命题者设置了问题(Ⅰ):讨论函数f(x)=ax2-a-lnx的单调性.
为了增加试题难度,命题者考虑引入新函数,于是构造了过点(1,0)的函数g(x)=1x-e1-x.
由于动函数f(x)与定函数g(x)相交于点(1,0).于是考虑比较f(x)与g(x)在定点两侧函数值的大小.为减小试题的难度,命题者只研究两个函数在定点右侧的情况,即研究x>1时,两函数值的大小关系.
如图3,当a≤0时,函数f(x)的图像恒在函数g(x)图像的下方.
图3图4图5如图4,当a>0且12a≤1时,函数f(x)图像恒在函数g(x)图像的上方.
如图5,当a>0且12a>1时,函数f(x),g(x)的图像有异于点(1,0)的又一交点(p,q).
当1
根据上述分析,命题者设置了问题(Ⅱ):确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.
此类问题的命题手法为:研究过同一定点的两个函数(其中一个为动函数,一个为定函数)的函数图像关系,并从中提炼设置问题.
如能探明试题的命题方法,解题者就不难得到解题思路了.讲题时,也将有利于教师讲清问题的来龙去脉.
3命制新题
基于对2016年高考四川卷理科函数导数试题命题手法的研究.模仿此命题手法,笔者尝试编制新题.
新题1:已知函数f(x)=ex-ax有极值1.
(Ⅰ)求实数a,并确定该极值为极大值还是极小值;
(Ⅱ)当x∈0,+∞)时,f(x)≥mxln(x+1)+1恒成立,求实数m的取值范围.
解(Ⅰ)f′(x)=ex-a.
①当a≤0时,f′(x)>0,f(x)在(-∞,+∞)上单调递增,无极值,不符合题意;
②当a>0时,f′(x)=0,x=lna,当x∈(-∞,lna)时,f′(x)<0,f(x)单调递减;
当x∈(lna,+∞)时,f′(x)>0,f(x)单调递增.
当x=lna时,f(x)取到极小值,f(lna)=a-alna=1,得a=1.
(Ⅱ)f(x)=ex-x.
令g(x)=ex-x-mxln(x+1)-1,x∈[0,+∞),g′(x)=ex-1-mln(x+1)-mxx+1.
构造函数h(x)=ex-1-mln(x+1)-mxx+1,x∈[0,+∞),h′(x)=ex-m1(x+1)2+1x+1,h′(0)=1-2m.
①当m≤0时,h′(x)>0,h(x)在0,+∞)上单调递增,h(x)min=0,则g′(x)>0,g(x)单调递增,g(x)min=0,
所以g(x)≥0,故ex-x≥mxln(x+1)+1恒成立.
②当0
新题2:已知函数f(x)=x2-x,g(x)=ex-ax-1.
(Ⅰ)讨论函数g(x)的单调性;
(Ⅱ)当x>0时,f(x)≤g(x)恒成立,求实数a的取值范围.
解(Ⅰ)g′(x)=ex-a.
①当a≤0时,g′(x)>0,g(x)在(-∞,+∞)上单调递增;②当a>0时,当x∈(-∞,lna)时,g′(x)<0,g(x)单调递减,当x∈(lna,+∞)时,g′(x)>0,g(x)单调递增.
作者简介杨苍洲(1979—),男,福建泉州人,中学一级教师,研究方向:数学教学,命题研究.泉州市中小学名师工作室成员,福建省第二届教师教学技能大赛特等奖者.多次参与泉州市质检命题,福建省质检命题,福建省高考命题.在中数期刊发表文章200多篇.
崔红光(1981—),女,福建泉州,中学一级教师,研究方向:数学教学,命题研究.曾获得泉州市说课比赛二等奖,泉州市普通高中高考九科试卷命制技能比赛二等奖.

