基于FPGA硬件实现高斯随机数生成研究
王华华+杨康+余永坤

摘要:在信息通信安全领域内,密钥的安全性直接影响公开加密算法的安全性,而密钥的安全性又与随机数的产生及其随机性能的优良息息相关,所以随机数的作用就变得非常的重要。文章基于FPGA硬件来实现高斯随机数生成,算法实现总体共分为两部分,第一部分采用CombinedTausworthe算法实现产生均匀分布的随机数序列;第二部分为BoxMulle算法,利用两组均勾分布的随机数通过转换来产生高斯随机数。产生的随机数的随机性表现良好。高斯随机数目前是应用最为广泛的一类随机数,所以对FPGA的高斯随机数生成器的研究具有非常重要的实际意义。
关键词:随机数;CombinedTausworthe算法;BoxMulle算法
随着信息技术和计算机网络技术的高速发展,通信网络系统己经成为当下社会发展的重要基础设施。网络通信己逐渐发展成为人们进行信息交流的必要途径,数字技术己经深入到了人们的日常生活和生产当中。在这个信息化的时代,人们可以迅速而方便地在网上查找各种想要的信息,比如实时和未来几天的天气预报,国家两会提出的新政策,旅游攻略,酒店预订,网上购票等,给人们生活带来了诸多便利。与此同时,在信息安全领域的隐患也慢慢地显现出来。近年来互联网高速的发展,由于信息安全引发的问题也越来越多,各种安全问题直接限制了某些应用的出现。这些问题不仅关系到个人的隐私安全问题,还关系到商业中的机密,导致不正当的商业竞争,还关系到国家机密的保全等重要问题。所以加密就自然而然成為保护信息的一个重要手段,加密算法的安全性也变得非常的重要[1]。
对数据安全加密,对知识产权坚决保护成为在信息安全领域必要的举措。在信息通信安全领域内,密钥的安全性直接影响公开加密算法的安全性。而密钥的安全性又与随机数的产生及其随机性能的优良息息相关,所以随机数的作用就变得非常重要。加密算法是信息安全领域的核心,除此之外,加密算法在网络通信也被广泛使用。为了保证通信的安全性,需要进行多种身份认证,避免信息泄露造成的可能性损失等,在安全性要求很高的场合中必须采用随机性非常好的随机数来进行加密,因此随机数的生成就变成了一个非常重要且不能缺少的环节。所以为了生成高安全性的随机序列和保持其良好的生成性能,保证加密算法的有效性,需要我们对生成随机序列的方法进行更加深入和细致的研究。
国内外的研究机构一直都在重点研究随机序列的产生方法与其随机性的测试,但是其产生方法只有两种:(1)真随机数,通过物理的方法来产生真正的随机数;(2)伪随机数,主要运用数学的方法来生成。真随机数是源于物理世界的真实随机源,其主要特征是不易被破解,所以安全性非常高,因此其在数据加密、身份鉴定和密钥管理等领域有着广泛的应用。伪随机序列主要特征是使用方便且很容易获取,所以大多用于测试、仿真等领域。
目前对伪随机序列的研究现状可大致分为两大类:(1)伪随机序列可以直接由数学理论构造;(2)由LFSR构造出的伪随机序列[2]。第一类构造的伪随机序列在理论上能够很容易分析序列的随机性能,但是其实现会有很大问题,主要是构造难度非常大,而且成本和实现的代价不成比例。而基于LFSR构造的伪随机序列和理论序列则在实际应用中比较容易实现,而且成本较低,性能较优。
1整体架构
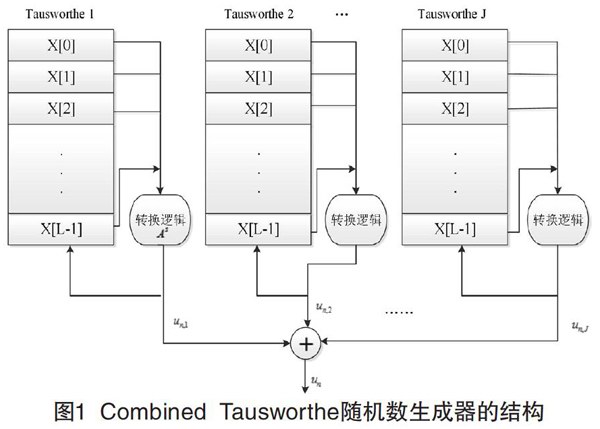
Combined Tausworthe随机数生成器的结构如图1所示。
由该结构产生的随机数满足式(3)中的约束关系。最终的输出是J个Tausworthe随机数生成器输出的异或结果。每个Tausworthe随机数生成器是由一个L位的寄存器和转换逻辑,构成的。
2随机数产生算法
2.1均匀分布随机数产生算法
本文应用Combined Tausworthe算法产生的均句分布随机数,Combined Tausworthe随机数生成器由若干个Tausworthe随机数生成器组成[3],每个Tausworthe随机数生成器产生的随机数可以表示成如下形式:
其中,L和s是非零正整数,s表示跳变步长,L表示随机数的输出位宽。是一个随机序列,其递归关系式为:
其中,特征多项式的系数。当为本原多项式时,输出序列的周期可以取得最大值:通常取如下的三项式:。
由J个Tausworthe随机数生成器构成的CombinedTausworthe随机数生成器产生的(0,1)区间内的均句分布随机数表示如下:
其中,是第J个Tausworthe随机数生成器对应的输出。由以及对应相等,即:
可得,其他为,带入(2)式化简如下:
2.2高斯随机数产生方法
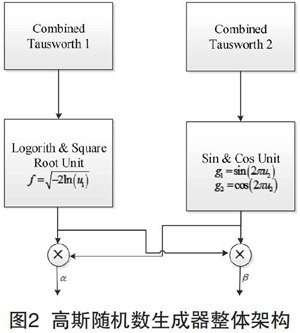
Box-Muller可以将产生的均匀分布随机数转换为高斯分布随机数,其依据的原理是:两组相互独立的高斯分布随机数的平方和是服从指数分布的,其转换过程表示为:
其中,是两路均勾分布的随机数,《和反是最终得到的高斯分布随机数,具体产生过程如图2所示。
输出位宽三的可配置性表现在参数组合,的选取上。设计Combined Tausworthe随机数生成器时,可以根据设计需求选取输出位宽L,得到满足“ME (Maxilnally Equidistributed)条件”的参数组合,需要指出的是,并不是所有的都能找到满足ME条件的,参数组合。当没有参数组合可以满足ME条件时,采取一个折中的办法:假设且,对应CT RNG满足Mli条件,那么可以选取该Combined Tausworthe随机数生成器输出中的三位作为新的输出,构成三位输出的RNG。所以,在设计Combined Tausworthe随机数生成器时,总可以根据实际需要来选取合适的输出位宽L实现硬件设计的可配置性。Combined Tausworthe详细参数如表1所示。
3总结
利用modelsim仿真工具对verilog代码进行仿真,得到的结果如图3所示。
将可执行程序植入开发板中,硬件生成随机数波形如机数波形如图4所示。
4结语
本次设计中的总体思路是分为两部分:第一部分是产生两路均匀分布的随机数,第二部分是利用这两路随机数进行转换而产生两路高斯分布的随机数[4]。第一部分采用了CombinedTausworthe算法实现产生均句随机数,其中最为关键的是状态转换逻辑矩阵的特征,设计了一种使用s个二输入异或门来实现的硬件结构,实现每个时钟周期内更新随机序列。第二部分采用BoxMuller算法实现转换,在硬件实现过程中采用添加IP核来实现数据运算,利用最值分析法和静态误差法确定各操作数的位宽来保证数据的正确性和精度。把生成的可执行程序导入开发板上,能实现快速产生随机数,硬件开销合理。硬件执行程序以后用txt文件的形式输出运行结果,利用sts-2.1.2软件包来测试txt文件随机数的随机质量,测试结果显示随机性良好。
[参考文献]
[1]蔡方旻,万民.基于FPGA的随机数生成器的设计与实现[J].江西通信科技,2014(1):42-44.
[2]吴飞,李艳萍.基于FPGA一种真随机数生成器的设计和实现[J].计算机应用与软件,2013(11):258-260,286.
[3]梁媛一种组合式随机数发生器的设计与实现[D].成都:电子科技大学,2016.
[4]谷晓忱,张民选一种基于FPGA的高斯随机数生成器的设计与实现[J]计算机学报,2011(1):165-173.

