汽车租赁调度模型的探求

    姚军 聂东升

    

    

    【摘 要】 本文是汽车租赁调度的线性优化问题。根据汽车租赁代理点之间不同种类汽车的调度费用作为建立目标规划的变量，控制总的调度费用最小为最终目标。建立汽车租赁调度的最优化模型，借用lingo软件对模型进行求解。以此求得在未来确定时间段内的汽车调度方案。

    【关键词】 线性规划 汽车调度 最优调度

    1 背景

    随着国内汽车租赁行业的兴起，许多公司的规模逐步扩大，代理点遍及很广，但不同地区对汽车数量的需求各不相同。据了解，目前，中国共有6300余家汽车租赁业户，租赁车辆总数约达20万辆，并以每年20%左右的速度增長，2018年中国汽车租赁行业市场规模更是超过了800亿元。随着汽车租赁公司的发展，竞争压力也随着增加，因此各个公司需要合理分配旗下各个代理点之间的汽车数量与各个代理点之间的最优调度方案，以降低成本获得更大的利润，同时提高自身得到竞争力。

    2 问题来源与分析：

    现有某城市有一家汽车租赁公司，此公司年初在全市范围内有379辆可供租赁的汽车，分布于20个代理点中。每个代理点的位置都以地理坐标X和Y的形式给出，单位为千米。假定两个代理点之间的距离约为他们之间欧氏距离（即直线距离）的1.4倍。

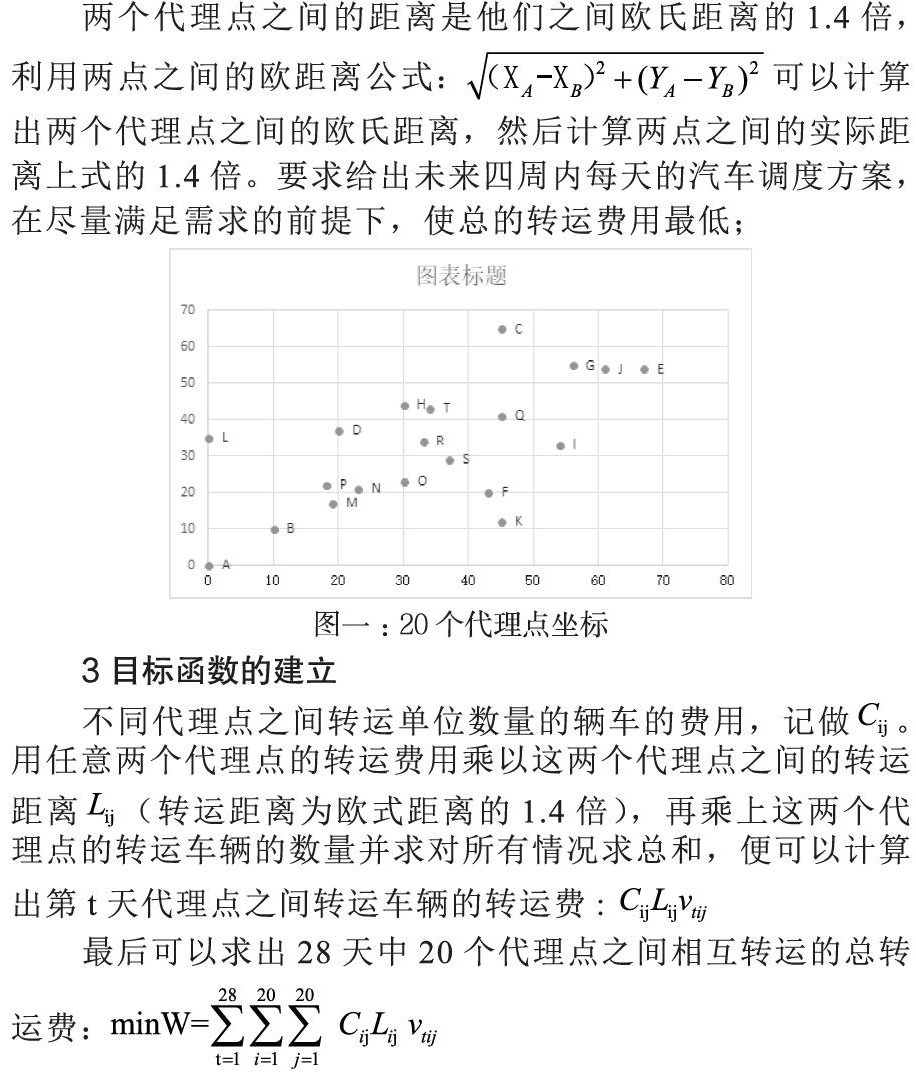
    两个代理点之间的距离是他们之间欧氏距离的1.4倍，利用两点之间的欧距离公式：可以计算出两个代理点之间的欧氏距离，然后计算两点之间的实际距离上式的1.4倍。要求给出未来四周内每天的汽车调度方案，在尽量满足需求的前提下，使总的转运费用最低;

    3 目标函数的建立

    不同代理点之间转运单位数量的辆车的费用，记做。用任意两个代理点的转运费用乘以这两个代理点之间的转运距离（转运距离为欧式距离的1.4倍），再乘上这两个代理点的转运车辆的数量并求对所有情况求总和，便可以计算出第t天代理点之间转运车辆的转运费：

    最后可以求出28天中20个代理点之间相互转运的总转运费：

    4 约束条件的建立

    设第t天所有代理点拥有的车辆总数为At，第t天所有代理点需求的车辆总数为Bt，当一天中所有代理点的总需求量大于或者等于所有代理点实际拥有的车辆总数的时，即：，根据题目要求，要尽量满足各代理点的汽车需求，所以，经调度后，一定要保证这一天中各代理点的汽车需求数都大于或等于各代理点实际拥有的车辆数。所以有如下约束条件：

    C由于没有购置新车，也不考虑汽车的缺损，所以对于任一天所有代理点的车辆拥有数之和应该等于379，所以有如下约束条件：

    D对于某天的某代理点而言，当天转运进来的总车辆数与其转运出去的总车辆数之差应该等于该天该代理点拥有的车辆数与前一天拥有车辆数的差，所以有如下约束条件：

    最终的模型如下：

    5 结语

    对于建立的线性规划模型，可以得出任意两个代理点之间的转运数量。通过LINGO软件进行编程所解得的结果可信，并且符合实际。但是由于在计算中忽略了汽车调度花费的时间，所以应用在在实际生活中，应尽量使汽车调度花费的时间少，以免影响第二天的汽车租赁服务。该模型同样适用于人员的调动问题。例如，某地区共有10所小学，由于一些原因导致一些学校缺少教师，另一些学校教师有多余，就存在着合理调配教师，尽量使这10个学校的老师数量接近教师编制数量，提高该地区整体的教学质量。该模型在实际生活中有比较广泛的应用，可结合实际加以应用。

    【参考文献】

    [1] 刘浩，韩晶.MATLAB R2016a完全自学一本通[M].电子工业出版社，2016，p274-275.

    [2] 司守奎.孙兆亮.数学建模算法与应用（第2版）.北京：国防工业出版社，2015：1-37，p20-46

    [3] 熊彬.汽车租赁管理信息系统的设计与实现[D].江西财经大学， 2018.

    [4] 蒋步健.共享租赁模式下的汽车供需匹配问题研究[D].合肥工业大学， 2017.

    作者简介：姚军，男，主要研究方向：数学建模在实际生活中的运用。

    通讯作者：聂东升，男，主要研究方向：水利水电工程。