等效思维在初中物理解题中的合理运用
姬鸣亚

等效思维法在初中物理题目中的应用能够有效地将复杂的问题简单化,化难为易.学生在解题过程中使用这种方法能够简化解题过程,提高解题速度,同时能够在解题过程中活跃自身的解题思维,提高学生的创新能力.
1等效变换简化问题
等效变换是初中物理解题中比较常用的一种方法,并且经常用于电路的变换.如将比较复杂的电路等效变换成一些比较明确的串联等效电路或者并联等效电路.等效变换的过程可以通过添加辅助线、增加平衡力等方式来进行变换,使得解题思路明朗化,简化解题步骤.
例题1如图1所示,其中电源电动势为6 V,内电阻忽略不计,电路中的电阻除了R1,电阻阻值都为R,已知电阻R1为9 Ω,电路消耗的总功率是10 W,如果将电路中的R1换成阻值为3 Ω的电阻R2,则此电路消耗的总功率为多少Ω?
分析通过分析整个电路,可以将电路中的七个阻值都为R的电阻看成一个整体,并且其与电阻R1并联,因此经过等效变换,可以将电路图简化成图2所示,因此可以得出公式P=ε2(R1+R0)R1R0,已知P1=10 W,ε=6 V,因此可以求出R0=6 Ω,因此当变成R2时,代入上述公式可得P2=18 W.
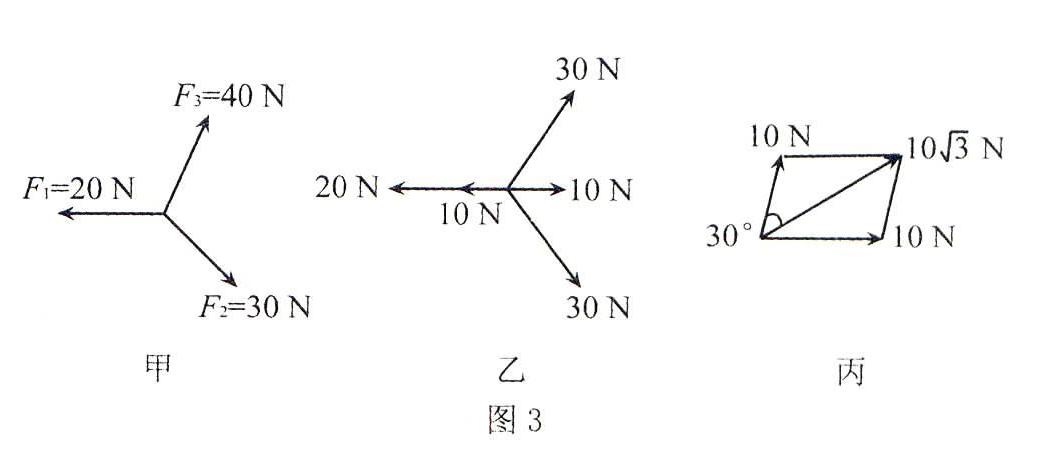
例题2如图3所示,F1、F2、F3为三个共面共点力,相互成120°角,已知F1为20 N,F2为30 N,F3为40 N,求合力的大小和方向.
分析如果按照一般解法,通过力的平行四边形合成法则来求解,会发现解题的过程非常复杂,但如果通过等效变换,则能够简化步骤.具体过程是沿着力F1的方向上加上一个大小为10 N的力,同时反向也加上一个10 N的力,然后将F3看做一个30 N和一个10 N的合力,如图3丙,此时变换后的六个共点力的作用和原来的效果相同,通过观察发现三个30 N的力互成120°,合力为零.因此系统中只剩下两个互成60°的10 N的力,可以得出其合力大小为103 N,方向在题目中图3中的F2、F3之间,与F3之间的夹角为30°.
2等效替代简化问题
在分析较为复杂的物理问题时,运用等效替代法能够有效简化问题.
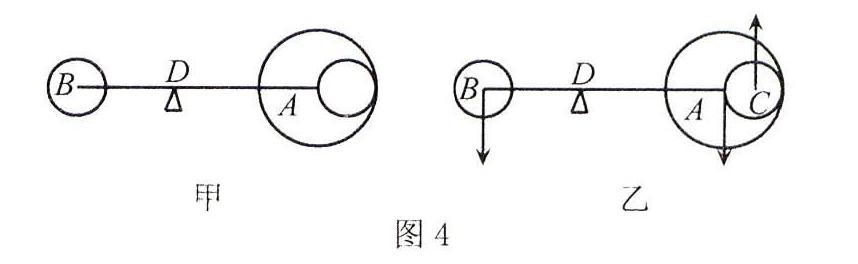
例题3如图4甲所示,现有等臂杠杆AB,其两端都固定有相同材料的圆板.已知A端固定的圆板的半径为R,圆板上有一个半径为r的小孔,r=R/2,其中OA=2R,问要使杠杆处于平衡状态,杠杆B端圆板的半径为多大?
分析常规的解法是首先计算杠杆A端圆板的重心位置, 但这种计算方法非常麻烦, 如果使用等效替代意义.例2的实验目的是“测量小灯泡的额定功率”,三次实验的灯泡两端电压均应为额定电压3.8 V,则对应电流值应当相同才对,但表格中的电流值变化不大,是实验误差吗?由于小灯泡的额定电压是3.8 V,所以电压表应当选择15 V量程,分度值为0.5 V,因为小灯泡的额定电压不是电压表的整数刻度,导致调节电压为额定电压时很容易产生误差,所以小华采取多次实验取平均值的方法来减小误差,实验方案应该是合理的.
通过对两道例题的分析可以看出,学生在解答此类问题时,应通过比较分析,准确把握问题情境和条件的变化,充分利用“思维定势”的同时,要突破“思维定势”对问题解决的消极影响,利用处理过类似的旧问题的知识和经验处理新问题,缩短思考时间,提高解决问题的效率.法,则能够省去这些复杂的计算.已知A板上挖有一孔,在解题时可以将其等效成没有挖孔,而是一个大小等于挖去部分重力的力F沿着竖直向上的方向上作用在孔心C上(图4乙),然后根据力矩平衡条件很容易就能计算出来,通过力来代替能够很好的简化解题过程.
3等效假设简化问题
很多物理题目给出的条件和问题都比较隐晦,在解题过程中很容易复杂化,对于这些类型的问题可以通过等效假设的方式来将这些隐含的问题暴露出来,从而简化问题.
例题4如图5所示,该电路中的电源电动势为ε,内电阻为r,R1是定值电阻,R2是变阻器,问R2的值为多少时,变阻器R2上消耗的电功率最大,最大为多少?
分析常规解法很复杂,但通过等效假设可以简化问题,解题时可以将图5的虚线框中的部分看成电源,此时R1也变成了电源的内阻部分,R2则是电路中唯一的外电阻.由此可求出电路的等效电阻为r′=R1rR1+r,等效电动势为外电路R2断开图5中的虚线框两端的电压ε′=U=R1εR1+r,根据题中要求的电源输出最大功率可以得出,当R2=r′=R1rR1+r时,变阻器R2上消耗的功率最大,从而求出题目中的答案.
4等效类比简化问题
等效类比主要是通过分析不同物体在某些方面的等效性,进而得出其在其他方面也具有等效性.这种方法能够开阔思路,灵活的找出解题方法.
例题5如图6所示,现有一端固定在P点一端连接质量为m的小球A的轻质弹簧,弹簧的倔强系数为K,系统处于静止状态.已知质量为M的球B以v0的速度和球A发生碰撞,碰撞后两个球一起在光滑的水平面上向p点方向运动,经过一段时间后又往回运动,当A球到达某个位置时B球脱离A球独自运动,求A球和B球从接触到脱离接触所用的时间.
分析两个球完全非弹性碰撞,碰撞后做变加速运动,初看这种题目感觉似乎找不到解题的方法,但仔细分析两球接触到脱离过程中受力情况,就会发现其受力情况和弹簧振子的受力情况一致,因此在解题时可以将两个小球共同运动的时间等效成一个弹簧振子完成半个周期振动需要的时间.通过求弹簧振子运动周期T=mK,可以很容易求出等效时间t=T2.
总之,等效思维在初中物理的学习中发挥着重要的作用,教师在教学中必须合理安排例题,让学生灵活掌握这种思维方法的应用,促进学生创新思维的发展,提高学生的物理解题能力.



等效思维法在初中物理题目中的应用能够有效地将复杂的问题简单化,化难为易.学生在解题过程中使用这种方法能够简化解题过程,提高解题速度,同时能够在解题过程中活跃自身的解题思维,提高学生的创新能力.
1等效变换简化问题
等效变换是初中物理解题中比较常用的一种方法,并且经常用于电路的变换.如将比较复杂的电路等效变换成一些比较明确的串联等效电路或者并联等效电路.等效变换的过程可以通过添加辅助线、增加平衡力等方式来进行变换,使得解题思路明朗化,简化解题步骤.
例题1如图1所示,其中电源电动势为6 V,内电阻忽略不计,电路中的电阻除了R1,电阻阻值都为R,已知电阻R1为9 Ω,电路消耗的总功率是10 W,如果将电路中的R1换成阻值为3 Ω的电阻R2,则此电路消耗的总功率为多少Ω?
分析通过分析整个电路,可以将电路中的七个阻值都为R的电阻看成一个整体,并且其与电阻R1并联,因此经过等效变换,可以将电路图简化成图2所示,因此可以得出公式P=ε2(R1+R0)R1R0,已知P1=10 W,ε=6 V,因此可以求出R0=6 Ω,因此当变成R2时,代入上述公式可得P2=18 W.
例题2如图3所示,F1、F2、F3为三个共面共点力,相互成120°角,已知F1为20 N,F2为30 N,F3为40 N,求合力的大小和方向.
分析如果按照一般解法,通过力的平行四边形合成法则来求解,会发现解题的过程非常复杂,但如果通过等效变换,则能够简化步骤.具体过程是沿着力F1的方向上加上一个大小为10 N的力,同时反向也加上一个10 N的力,然后将F3看做一个30 N和一个10 N的合力,如图3丙,此时变换后的六个共点力的作用和原来的效果相同,通过观察发现三个30 N的力互成120°,合力为零.因此系统中只剩下两个互成60°的10 N的力,可以得出其合力大小为103 N,方向在题目中图3中的F2、F3之间,与F3之间的夹角为30°.
2等效替代简化问题
在分析较为复杂的物理问题时,运用等效替代法能够有效简化问题.
例题3如图4甲所示,现有等臂杠杆AB,其两端都固定有相同材料的圆板.已知A端固定的圆板的半径为R,圆板上有一个半径为r的小孔,r=R/2,其中OA=2R,问要使杠杆处于平衡状态,杠杆B端圆板的半径为多大?
分析常规的解法是首先计算杠杆A端圆板的重心位置, 但这种计算方法非常麻烦, 如果使用等效替代意义.例2的实验目的是“测量小灯泡的额定功率”,三次实验的灯泡两端电压均应为额定电压3.8 V,则对应电流值应当相同才对,但表格中的电流值变化不大,是实验误差吗?由于小灯泡的额定电压是3.8 V,所以电压表应当选择15 V量程,分度值为0.5 V,因为小灯泡的额定电压不是电压表的整数刻度,导致调节电压为额定电压时很容易产生误差,所以小华采取多次实验取平均值的方法来减小误差,实验方案应该是合理的.
通过对两道例题的分析可以看出,学生在解答此类问题时,应通过比较分析,准确把握问题情境和条件的变化,充分利用“思维定势”的同时,要突破“思维定势”对问题解决的消极影响,利用处理过类似的旧问题的知识和经验处理新问题,缩短思考时间,提高解决问题的效率.法,则能够省去这些复杂的计算.已知A板上挖有一孔,在解题时可以将其等效成没有挖孔,而是一个大小等于挖去部分重力的力F沿着竖直向上的方向上作用在孔心C上(图4乙),然后根据力矩平衡条件很容易就能计算出来,通过力来代替能够很好的简化解题过程.
3等效假设简化问题
很多物理题目给出的条件和问题都比较隐晦,在解题过程中很容易复杂化,对于这些类型的问题可以通过等效假设的方式来将这些隐含的问题暴露出来,从而简化问题.
例题4如图5所示,该电路中的电源电动势为ε,内电阻为r,R1是定值电阻,R2是变阻器,问R2的值为多少时,变阻器R2上消耗的电功率最大,最大为多少?
分析常规解法很复杂,但通过等效假设可以简化问题,解题时可以将图5的虚线框中的部分看成电源,此时R1也变成了电源的内阻部分,R2则是电路中唯一的外电阻.由此可求出电路的等效电阻为r′=R1rR1+r,等效电动势为外电路R2断开图5中的虚线框两端的电压ε′=U=R1εR1+r,根据题中要求的电源输出最大功率可以得出,当R2=r′=R1rR1+r时,变阻器R2上消耗的功率最大,从而求出题目中的答案.
4等效类比简化问题
等效类比主要是通过分析不同物体在某些方面的等效性,进而得出其在其他方面也具有等效性.这种方法能够开阔思路,灵活的找出解题方法.
例题5如图6所示,现有一端固定在P点一端连接质量为m的小球A的轻质弹簧,弹簧的倔强系数为K,系统处于静止状态.已知质量为M的球B以v0的速度和球A发生碰撞,碰撞后两个球一起在光滑的水平面上向p点方向运动,经过一段时间后又往回运动,当A球到达某个位置时B球脱离A球独自运动,求A球和B球从接触到脱离接触所用的时间.
分析两个球完全非弹性碰撞,碰撞后做变加速运动,初看这种题目感觉似乎找不到解题的方法,但仔细分析两球接触到脱离过程中受力情况,就会发现其受力情况和弹簧振子的受力情况一致,因此在解题时可以将两个小球共同运动的时间等效成一个弹簧振子完成半个周期振动需要的时间.通过求弹簧振子运动周期T=mK,可以很容易求出等效时间t=T2.
总之,等效思维在初中物理的学习中发挥着重要的作用,教师在教学中必须合理安排例题,让学生灵活掌握这种思维方法的应用,促进学生创新思维的发展,提高学生的物理解题能力.

