基于音频信号的数字滤波器设计实验
欧阳华+杨忠林+周卫平
[摘 要]数字滤波器设计是数字信号处理实验教学的重要内容,传统的滤波器设计实验根据给定的技术指标,设计出满足该指标的系统函数,并通过观察系统的频率响应验证滤波性能。教师可以通过设计基于声音信号的数字滤波实验,将正弦噪声加入音乐信号中,让学生自主设计一个简单的陷波器滤除正弦噪声,通过听觉验证是否达到滤波效果。教学实践证明,采用声音信号作为滤波对象,使得实验过程完整直观,既深化了学生对滤波器设计原理的理解,也锻炼了学生自主设计能力。
[关键词]数字滤波器;声音信号;陷波器
[中图分类号] TN713+.7 [文献标识码] A [文章编号] 2095-3437(2017)04-0006-03
引言
数字滤波是数字信号处理技术最典型的应用之一,与此对应数字滤波器设计实验是“数字信号处理”教学重要的环节,它通过计算机仿真的方法将理论设计过程用Matlab程序语言完成,简化步骤和计算,加深对设计方法的理解。常规的滤波器设计实验根据给定滤波器的性能要求,用一个因果稳定的离散线性移不变的系统函数H(z)去逼近这一性能要求。也就是说,实验的目的是设计出满足给定技术指标的数字系统函数H(z),或者是单位冲激响应h(n),然后画出该系统在特定频率范围的频率响应曲线,验证该系统是否达到技术指标。该基本实验从技术指标开始,到系统函数结束,由一组数据得到另一组数据,是滤波器设计的核心工作。但实验过程不完整,实验对象不具体,在提出问题,分析问题,解决问题环节中,只体现了解决问题的数学方法。完成实验后学生会感到困惑,为什么这样的H(z)就能实现滤波,它的滤波性能到底如何呢?
结合我校自主研究实验项目,在传统滤波器设计实验的基础上,本文设计了一个加入正弦噪声的音乐信号作为系统输入的数字滤波实验。针对带噪声的音乐信号这个具体对象,学生自己确定要解决什么问题,解决问题思路和方法,判断问题是否解决。结果表明该滤波器设计实验效果良好,学生借助人耳这个天然的“傅里叶分析仪”感受到所设计的滤波器的滤波效果,加深了学生对滤波器原理的理解,促进了对滤波器设计方法的掌握。
一、数字滤波器设计原理

允许某些信号分量(有用信号)通过、同时阻止其他分量信号(噪声)通过的系统称为滤波器。在本科阶段只讨论信号和噪声处于不同的频率范围的加性噪声,即信号和噪声是叠加在一起的。在LSI系统分析理论中,输出信号y(n)是输入信号x(n)与系统单位冲激响应h(n)的卷积:
在实际应用中,为了采用因果稳定的IIR系统或FIR系统来逼近理想特性,对理想频率特性的要求适当放宽,具体表现为在通带和阻带之间引入一个过渡带,并允许幅度响应在通带和阻带有一定的波动。以物理可实现的因果稳定低通滤波器为例,其幅度特性如图2所示。理想滤波器的截止频率放宽为两对技术指标:通带截止频率ωp和通带容限δp;阻带截止频率ωs和阻带容限δs。为了便于表示,通常使用通带允许的最大衰减Ap=-201g(1-δp)和阻带应达到的最小衰减As=-201g(1-δs)来描述通带和阻带容限。
二、一个简单的陷波滤波器设计
为帮助学生理解滤波器的功能和设计原理,我们设计了一个基于音频信号处理的数字滤波实验。实验对象是加入单频正弦噪声的音频信号,实验目的是设计一个简单的IIR滤波器滤除正弦噪声。根据实验目的,我们应该设计一个截止频率在正弦噪声附近的带阻滤波器。带阻滤波器的阻带在整个频率范围的中间部分,这样的频率响应不可能由一个一阶实系数系统函数产生,故其阶次至少为2阶。
设噪声频率是ω0,这样我们可以选择一个形如(1-2cosω0z-1+z-2)的二阶多项式作为系统函数分子的一个因式,从而在中间频率段的ω0处为系统函数设计了一个零点,这将强迫幅度函数在ω0处为零。这时的频率ω0就是陷波频率,该滤波器就是陷波滤波器。该陷波滤波器的系统函数的形式如下[1]:
可见Matlab运行结果与理论计算是一致的。
更简单直观的滤波器设计方法是调用滤波器设计和分析工具箱。滤波器设计和分析工具箱(Filter Design and Analysis Tool (FDATool))是快速设计和分析滤波器的强大的图形用户界面,它不需要编程,只要通过菜单操作,进行指标参数选择就可以设计出满足要求的各种类型滤波器。
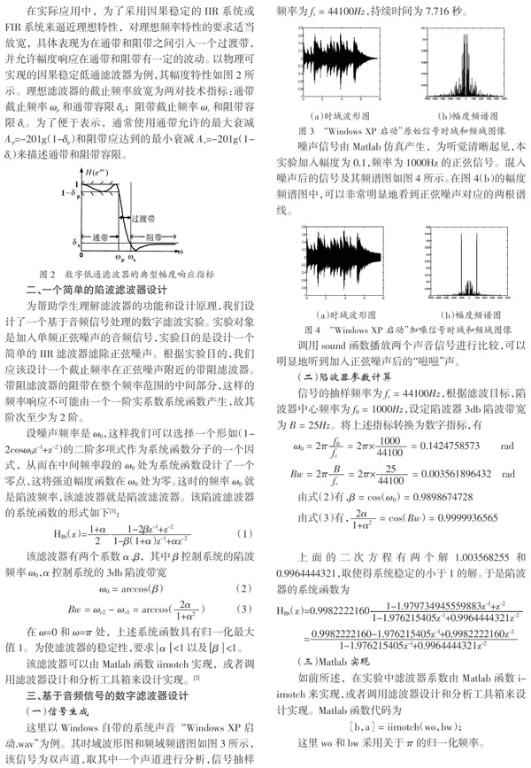
对于本例的参数设置步骤如下:(1)响应类型(“Response Type”)选择最后一项下拉框中的“Notching”;设计方法(“Design Method”)选择IIR下拉菜单中的“Single Notch”。该步骤确定了将采用单一频率的陷波器来实现滤波功能。(2) 在频率指标(“Frequency Specifications”)文本框中设定技术指标,以Hz为单位,信号抽样频率Fs = 44100,陷波频率为Fnotch =1000,带宽为Bandwidth=25。(3)在幅度指标(“Magnitude Specifications”)文本框中设定带宽增益为Apass=3。上述设置工作完成之后,按下“Design Filter”按钮,结果就出来了!参数设置和频率响应如图5所示。
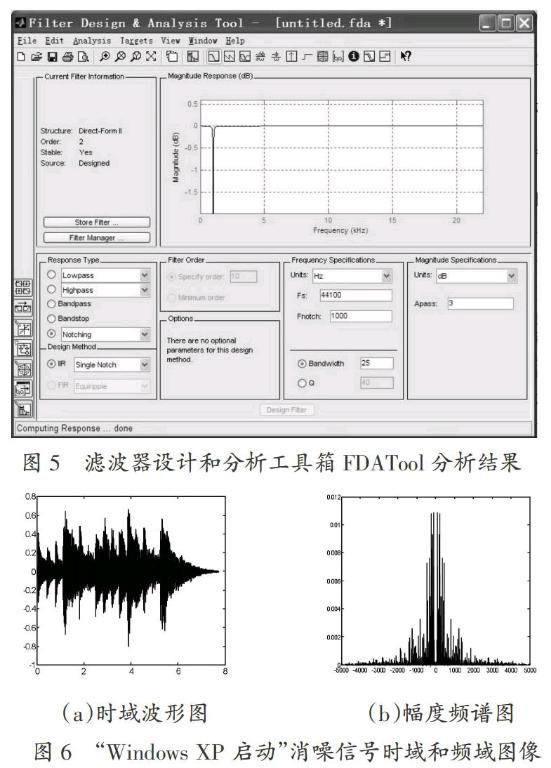
得到陷波器的分子、分母系数向量b、a后,调用filter函数对混入噪声后的信号进行滤波,滤波后的信号及其频谱图如图6所示。从图6(b)中的幅度频谱图可以观察到噪声已经滤除。听觉上也能够直接感受到滤波后的音频信号。
示例中的单频噪声滤波也可以采用一般的带阻滤波器实现,如IIR椭圆滤波器、海明窗FIR滤波器等。[3]相对于一般的带阻滤波器,陷波器具有计算简单、阶次低,频率选择性好等优点。如果噪声是多个单频正弦信号的叠加,例如同时加入1000Hz和2000Hz的噪声,则可以设计两个陷波频率分别为1000Hz和2000Hz的陷波器,再将两个陷波器级联形成一个四阶的带阻滤波器。
四、结语
综上所述,基于声音信号的数字滤波器设计改善了传统的滤波器设计方式,能够从听觉上让学生直接感受到铝箔效果。教学实践证明,采用声音信号作为滤波对象,使得实验过程完整直观,既深化了学生对滤波器设计原理的理解,也锻炼了理论联系实际的自主设计能力。
进一步的工作可以在音频信号中加入多频率噪声或色噪声,并考虑加入噪声的类型,以及噪声和信号的频谱的相对位置。在加入相同的噪声频谱的情况下,比较经典滤波、维纳滤波和自适应滤波等不同的滤波方法的效果。
[ 参 考 文 獻 ]
[1] Sanjit K. Mitra著,孙洪等译. 数字信号处理——基于计算机的方法(第三版)[M].北京:电子工业出版社,2006.
[2] 欧阳华,尹为民,邵英.基于比较教学法的FIR数字滤波器设计实验[J].电气电子教学学报,2011(1):75-77.
[3] 申艳,陈后金,薛健,等. 基于Matlab 加噪语音的FIR 滤波器设计[J].电气电子教学学报,2011(2):41-44.
[特约编辑:黄紧德]
[摘 要]数字滤波器设计是数字信号处理实验教学的重要内容,传统的滤波器设计实验根据给定的技术指标,设计出满足该指标的系统函数,并通过观察系统的频率响应验证滤波性能。教师可以通过设计基于声音信号的数字滤波实验,将正弦噪声加入音乐信号中,让学生自主设计一个简单的陷波器滤除正弦噪声,通过听觉验证是否达到滤波效果。教学实践证明,采用声音信号作为滤波对象,使得实验过程完整直观,既深化了学生对滤波器设计原理的理解,也锻炼了学生自主设计能力。
[关键词]数字滤波器;声音信号;陷波器
[中图分类号] TN713+.7 [文献标识码] A [文章编号] 2095-3437(2017)04-0006-03
引言
数字滤波是数字信号处理技术最典型的应用之一,与此对应数字滤波器设计实验是“数字信号处理”教学重要的环节,它通过计算机仿真的方法将理论设计过程用Matlab程序语言完成,简化步骤和计算,加深对设计方法的理解。常规的滤波器设计实验根据给定滤波器的性能要求,用一个因果稳定的离散线性移不变的系统函数H(z)去逼近这一性能要求。也就是说,实验的目的是设计出满足给定技术指标的数字系统函数H(z),或者是单位冲激响应h(n),然后画出该系统在特定频率范围的频率响应曲线,验证该系统是否达到技术指标。该基本实验从技术指标开始,到系统函数结束,由一组数据得到另一组数据,是滤波器设计的核心工作。但实验过程不完整,实验对象不具体,在提出问题,分析问题,解决问题环节中,只体现了解决问题的数学方法。完成实验后学生会感到困惑,为什么这样的H(z)就能实现滤波,它的滤波性能到底如何呢?
结合我校自主研究实验项目,在传统滤波器设计实验的基础上,本文设计了一个加入正弦噪声的音乐信号作为系统输入的数字滤波实验。针对带噪声的音乐信号这个具体对象,学生自己确定要解决什么问题,解决问题思路和方法,判断问题是否解决。结果表明该滤波器设计实验效果良好,学生借助人耳这个天然的“傅里叶分析仪”感受到所设计的滤波器的滤波效果,加深了学生对滤波器原理的理解,促进了对滤波器设计方法的掌握。
一、数字滤波器设计原理

允许某些信号分量(有用信号)通过、同时阻止其他分量信号(噪声)通过的系统称为滤波器。在本科阶段只讨论信号和噪声处于不同的频率范围的加性噪声,即信号和噪声是叠加在一起的。在LSI系统分析理论中,输出信号y(n)是输入信号x(n)与系统单位冲激响应h(n)的卷积:
在实际应用中,为了采用因果稳定的IIR系统或FIR系统来逼近理想特性,对理想频率特性的要求适当放宽,具体表现为在通带和阻带之间引入一个过渡带,并允许幅度响应在通带和阻带有一定的波动。以物理可实现的因果稳定低通滤波器为例,其幅度特性如图2所示。理想滤波器的截止频率放宽为两对技术指标:通带截止频率ωp和通带容限δp;阻带截止频率ωs和阻带容限δs。为了便于表示,通常使用通带允许的最大衰减Ap=-201g(1-δp)和阻带应达到的最小衰减As=-201g(1-δs)来描述通带和阻带容限。
二、一个简单的陷波滤波器设计

为帮助学生理解滤波器的功能和设计原理,我们设计了一个基于音频信号处理的数字滤波实验。实验对象是加入单频正弦噪声的音频信号,实验目的是设计一个简单的IIR滤波器滤除正弦噪声。根据实验目的,我们应该设计一个截止频率在正弦噪声附近的带阻滤波器。带阻滤波器的阻带在整个频率范围的中间部分,这样的频率响应不可能由一个一阶实系数系统函数产生,故其阶次至少为2阶。
设噪声频率是ω0,这样我们可以选择一个形如(1-2cosω0z-1+z-2)的二阶多项式作为系统函数分子的一个因式,从而在中间频率段的ω0处为系统函数设计了一个零点,这将强迫幅度函数在ω0处为零。这时的频率ω0就是陷波频率,该滤波器就是陷波滤波器。该陷波滤波器的系统函数的形式如下[1]:
可见Matlab运行结果与理论计算是一致的。
更简单直观的滤波器设计方法是调用滤波器设计和分析工具箱。滤波器设计和分析工具箱(Filter Design and Analysis Tool (FDATool))是快速设计和分析滤波器的强大的图形用户界面,它不需要编程,只要通过菜单操作,进行指标参数选择就可以设计出满足要求的各种类型滤波器。
对于本例的参数设置步骤如下:(1)响应类型(“Response Type”)选择最后一项下拉框中的“Notching”;设计方法(“Design Method”)选择IIR下拉菜单中的“Single Notch”。该步骤确定了将采用单一频率的陷波器来实现滤波功能。(2) 在频率指标(“Frequency Specifications”)文本框中设定技术指标,以Hz为单位,信号抽样频率Fs = 44100,陷波频率为Fnotch =1000,带宽为Bandwidth=25。(3)在幅度指标(“Magnitude Specifications”)文本框中设定带宽增益为Apass=3。上述设置工作完成之后,按下“Design Filter”按钮,结果就出来了!参数设置和频率响应如图5所示。

得到陷波器的分子、分母系数向量b、a后,调用filter函数对混入噪声后的信号进行滤波,滤波后的信号及其频谱图如图6所示。从图6(b)中的幅度频谱图可以观察到噪声已经滤除。听觉上也能够直接感受到滤波后的音频信号。
示例中的单频噪声滤波也可以采用一般的带阻滤波器实现,如IIR椭圆滤波器、海明窗FIR滤波器等。[3]相对于一般的带阻滤波器,陷波器具有计算简单、阶次低,频率选择性好等优点。如果噪声是多个单频正弦信号的叠加,例如同时加入1000Hz和2000Hz的噪声,则可以设计两个陷波频率分别为1000Hz和2000Hz的陷波器,再将两个陷波器级联形成一个四阶的带阻滤波器。
四、结语
综上所述,基于声音信号的数字滤波器设计改善了传统的滤波器设计方式,能够从听觉上让学生直接感受到铝箔效果。教学实践证明,采用声音信号作为滤波对象,使得实验过程完整直观,既深化了学生对滤波器设计原理的理解,也锻炼了理论联系实际的自主设计能力。
进一步的工作可以在音频信号中加入多频率噪声或色噪声,并考虑加入噪声的类型,以及噪声和信号的频谱的相对位置。在加入相同的噪声频谱的情况下,比较经典滤波、维纳滤波和自适应滤波等不同的滤波方法的效果。
[ 参 考 文 獻 ]
[1] Sanjit K. Mitra著,孙洪等译. 数字信号处理——基于计算机的方法(第三版)[M].北京:电子工业出版社,2006.
[2] 欧阳华,尹为民,邵英.基于比较教学法的FIR数字滤波器设计实验[J].电气电子教学学报,2011(1):75-77.
[3] 申艳,陈后金,薛健,等. 基于Matlab 加噪语音的FIR 滤波器设计[J].电气电子教学学报,2011(2):41-44.
[特约编辑:黄紧德]

