提高解题效度的五种习惯
印冬建


近期,我市举行了中考模拟考试,笔者参与了试卷的批阅工作.批阅时,我们发现,一些同学因解题习惯差导致了大量失分,这让笔者十分痛心.为此,认真梳理了试卷中的“无谓失误”,并找出了与之对应的解题范例.在试卷讲评课上,对“无谓失误”精准点评的同时,还将这些规范的解题过程呈现,供学生观摩欣赏,彰显范例的“正向”示范作用.本文就结合笔者讲评中呈现的部分案例来谈谈学生应具备的五种良好解题习惯.
1审题标记,实现文图呼应
试题解答的第一关就是审题,它是学生解题的起点,也是成功解题的关键.初中数学的学科特点,决定了试题应具备学段特色和数学特色,一些试题除了有文字说明外,还配有与之对应的图形.因此,在初中阶段的数学考试中,审题绝不是简单地读题,在读的同时,我们应将文字信息中的关键词进行标记(标着重号或画线),同时,还应将文字信息在图形中对应标注,实现文图呼应,为分析和获取解题思路等做好基础性工作.
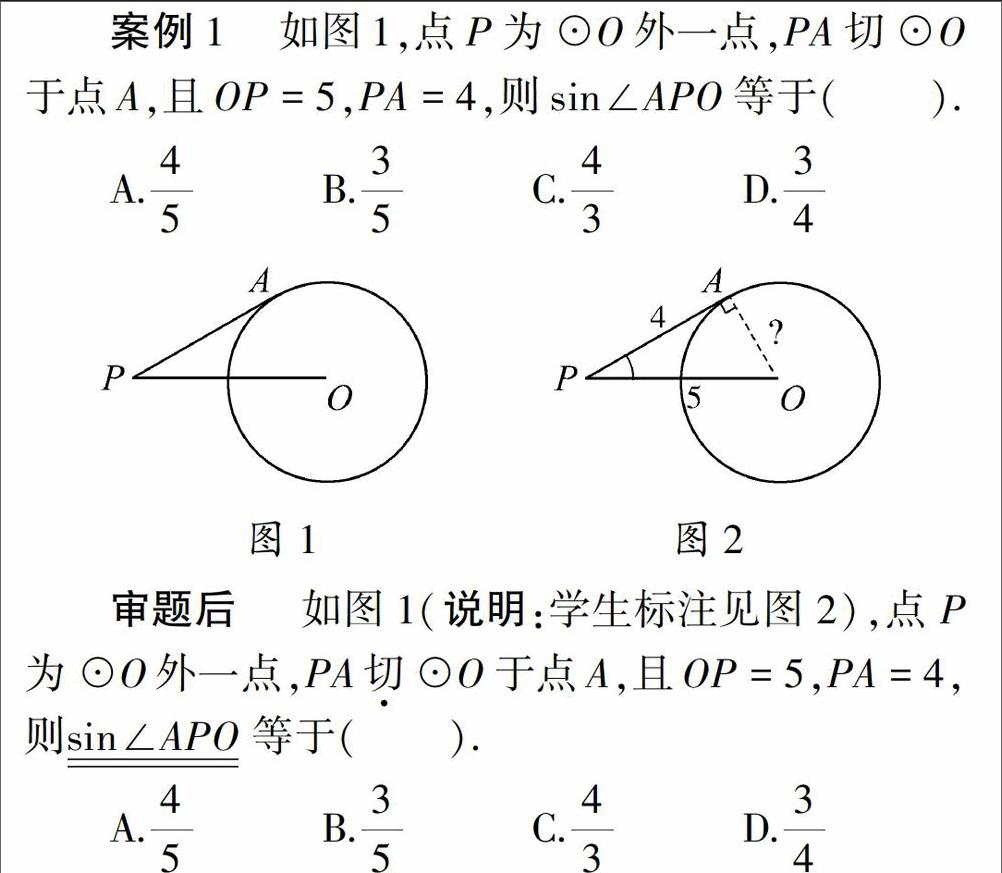
案例1如图1,点P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO等于().
A.45B.35C.43D.34
审题后如图1(说明:学生标注见图2),点P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO等于().
A.45B.35C.43D.34
案例分析这道试题条件并不多,一幅图,一段文字.这样的简单文图组合,让试题的解答看似十分简单.然而,如果不将题目中的文字信息和图形信息对应标注,这道试题的解答很可能会出现失误.事实也正如笔者所言,一些同学审题时,不仅文字中未做任何标记,连图形上也未进行标注,这样的解题习惯下选错答案并不意外.笔者呈现的这则范例中,学生审题后,将题中的几个关键信息“相切”(即题中的“切”)、“正弦”(sin)、“∠APO”等进行了标记,将“相切”通过“连接OA”和“标记直角”在图2中体现,将“OP=5,PA=4”在图中的相应线段旁进行了标注,将“∠APO”用“弧”在图中标注.这样的文图呼应,让试题条件和结论变得非常清晰,线段AO旁标注的“?”说明学生已经深刻领会了题意,并已经找到了正确的解题思路,问题很快得到化解!
2适时梳理,修正解题思路
在模拟考试和中考中,中等以上难度的试题散布在试卷的不同题型之中,这些试题常有“欲解不能,放手不甘”的感觉,解答中不可避免遇到一些“挫折”.面对此类的试题,当“解题不能”时,应及时梳理题中的条件和结论,反思解题思路分析中的得与失,发现被遗漏的条件并努力挖掘出隐含条件.这样的梳理,可以弥补“解题不能”状态下思路分析的“缺陷”,及时修正解题思路,从而找出正确的解法.
案例2试卷讲评课片断
如图3,在直角坐标系xOy中,直线y=mx与双曲线y=nx相交于点A和点B(b,-2),矩形OCDE的边CD恰好被点B平分,边DE交双曲线于F点,四边形OBDF的面积为2.求m,n的值.
教师:解答这道试题的关键是什么?
学生1:将“四边形OBDF的面积”转化为含有n的方程.
教师:怎么转化?
学生2:连接OD.根据“边CD恰好被点B平分”可得S△BOC=S△BOD=12n,根据矩形的对称性可得S△DOC=S△EOD=n,△EOF是“建构在双曲线和坐标轴上的直角三角形”,它的面积也是12n,所以,S四边形OBDF=n=2.
教师:非常棒,根据你的思路,接下来我们就可以顺利地求出m,n的值了!还有其他得到方程的方法吗?
学生陈述不同的方法,10分钟后,方法交流结束.
教师(看着学生3):老师发现你的解题过程有一些改动,解题时是不是走了一些“弯路”呀?能把你解答这道试题的经验与大家分享一下吗?
学生3:好吧!根据点的坐标的意义,我先将点B的坐标(b,-2)代入到y=nx中,得到-2=nb,整理得b=-12n,这样,我就用含有n的式子表示出了点B的坐标(-12n,-2).接下来,根据“顶点建构在坐标轴和双曲线上的直角三角形”面积求法,我用含有n的式子表示出了△BOC的面积为-12n.再往下,我有一种直觉,四边形OBDF的面积是△BOC的面积的2倍,但是我说不出理由.
教师:那你接下来是怎么做的呢?
学生3:我再读了一下题目.
教师:有什么新的发现吗?
学生3:刚才解题时,有个条件没看到.
教师:哪个条件?
学生:“CD恰好被点B平分”!这让我想到了“三角形的中线将三角形分割为两个面积相等的三角形”.所以,在连接OD后,得到了S△BOD=S△BOC=
-12n.此时,思路一下子就打开了.
教师:你还有什么发现?
学生3:△DOC和△DOE的面积相等,都是-n.我还发现了△EOF也是“顶点建构在坐标轴和双曲线上的直角三角形”,其面积也是-12n.到这儿,我发现△BOC的面积实际上与题目中所给的点B的坐标并没太大关系,所以,我删去了最初的解题过程,给出了和学生2差不多的解题过程!
教师:很好,你给我们大家做出了很好的示范!当我们解题遇到“障碍”时,就要和学生3一样,不要恐慌,重新梳理一下题目,细读文字,剖析图形,在“文图呼应”中找寻遗漏条件和隐含条件.充分利用这些条件,及时修正思路,正确的解法很快就能发现!
案例分析初次解题时,由于忽略“边CD恰好被点B平分”这一条件,让学生3的求解遇到了“障碍”,虽然写出了一些看似正确的过程,但始终无法求解.当他再度审题后,发现了这个条件,并且将它与已有知识“三角形的中线将三角形分割为两个面积相等的三角形”联系起来,找到了解题的辅助线.这样一来,“思路一下子就打开了”,隐含条件“△EOF是顶点建构在坐标轴和双曲线上的直角三角形”很快“浮出水面”,解题分析被拉回到“正道”.案例中,学生3经历了“遭遇困境—再度审题—脱困得解”的过程.事实上,每一名学生都有过这样的经历,然而能在“磨难”中形成良好的解题习惯的人却很少.基于此,在日常教学中,笔者经常会象案例2中这样,从学生的解题中挖掘出正反两面的教学资源,通过学生求解历程的自主陈述,在全班范围内分享解题的经验,突出“适时梳理”在问题解决中的作用,让这一解题行为成为学生的自觉习惯,提高学生分析问题和解决问题的能力.
3穷尽结论,力求踩点挣分
基于试题必须有一定区分度这一客观现实,与中考试题一样,模拟考试试题中也会存在一些用以控制满分的难题.因此,要求学生解答这些试题时,一定要有“宽容心”,允许自己出现无法求解的情形.作为考试,多挣分是考试的目标.试题解答时,当确实无法给出正确解题过程时,我们应尽可能多地将由条件可以得出的结论写出来,生成一些可能在“得分点”上的步骤,多少挽回一点“损失”.
案例3在分析下面这道试题时,笔者发现一些同学只给出了“零星”步骤,也得到了一些分数.
如图4,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形CDF,连接AF,DE.
(1)求证:AF=DE;(2)略.
命题者给出的第(1)题的评分标准如下:
证明:∵在梯形ABCD中,AB=CD,∴∠BAD=∠CDA(1分),∵△ABE和△DCF是等边三角形,∴AB=AE,DC=DF,∠BAE=∠CDF=60°,∴AE=DF(2分),∠EAB+∠BAD=∠FDC+∠CDA,即∠EAD=∠FDA(3分),∵AD=DA,∴△AED≌△DFA,∴AF=DE(4分).
学生1只写了一步:∵梯形ABCD中,AD∥BC,AB=CD,∴∠BAD=∠CDA.根据“评分标准”,阅卷老师给了1分.
学生2在给出学生1的过程的基础上,还增加了下面的步骤:
∵△ABE和△DCF是等边三角形,
∴AB=AE=BE=DC=DF=CF,∠BAE=∠ABE=∠AEB=∠CDF=∠CFD=∠DCF=60°.
学生2给出的解题过程,得到2分.
案例分析汽车组装车间,工人们将各种汽车零件紧密地整合在一起,就完成了一辆汽车的组装.数学解题与此类似,学生将不同的数学知识“链接”成一个整体,就形成了完整的解题过程.然而,无法回避的是,有时我们真不能将题中的所有知识“链接”起来.此时我们应告诉学生,不要灰心,出售汽车零件,同样可以实现其市场价值.数学解题亦然,数学知识也可以单独“销售获利”的.案例中的学生1,利用“等腰梯形同一底上两个底角相等”得出了“∠BAD=∠CDA”,拿到1分;学生2,不仅给出了学生1的过程,他还根据“等边三角形的三条边相等,三个角相等”得出了另外两组结论,顺利拿到2分.学生1、2紧扣题中的条件,生成的这些结论恰好都在本题的“得分点”上,阅卷老师的评判恰到好处地呈现出了这些考点的“价值”.因此,我们要鼓励学生在“解题无果”的情况下,将解题的中间过程尽可能多地呈现出来,以求踩在“得分点”上,实现所获知识的解题价值,拿到该拿的分数.
4重建图形,剔除干扰信息
数学考试中,综合问题一直都是学生解题的难点.这些试题一般包括题干和问题两部分,具有很强的综合性,信息量大,不仅包含丰富的文字信息,还有复杂的图形信息.试题一般会给出的两到三个问题,问题之间用并列或递进的方式衔接,存在着某种内在的联系.一般地,上一问题的顺利解决可能会为下一问题的求解提供一些有用的条件或共性的方法.因此,在试题解答时,不仅要从原题中捕捉有用的解题信息,还应从已经化解的数学问题中挖掘可用的条件或结论,将题目中与问题解决无关的条件剔除,简化问题情境,建构有效图形,让思路的分析和过程的书写不绕“弯子”、“干净利落”.
案例4如图5所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B,C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N,B,D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)略.
在试卷讲评时,一学生陈述了自己解答第(2)题的过程:
根据第(1)题得出的解析式和“BD与抛物线的对称轴交于点M”,求得点M的坐标为(2,1).然后,在草稿纸上作出草图,如图6.利用这幅“简图”,结合点M,C,D的坐标,我发现,△MCD是一个等腰直角三角形.根据这一发现,我在坐标轴上找到了三个符合要求的点N.在得出正确的解题思路后,回到答卷,我将符合要求的三个N点标注到答题纸的图上(即图5),并给出了完整的解题过程.
案例分析在数学考试中,复杂的问题情境,会成为很多学生解题的“障碍”.因此,为了让学生形成自主跨越“障碍”的能力,笔者将“重建图形”作为学生简化问题情境的“抓手”,通过日常教学的不断强化,促进学生形成解题应用的“惯性”.案例中,学生将与解决问题(2)无关的抛物线、抛物线的对称轴、直线AB等图形信息“剔除”,留下解题必备的“点B,D”和“△MCD”,形成图6.在无关信息被删除后,新图变得非常简单,对学生分析问题和解决问题十分有利.接下来,学生充分利用△MCD的特征,在新图中“找出了符合要求的三个点N”,并给出了完整的解题过程.这样的解题行为值得称赞,然而要想让学生能在考试中自觉生成这一行为,教师就必须通过解题教学对学生进行长期训练,训练方式很多,案例4中的求解过程的自主陈述是最常见的一种,通过分享“重建图形”解题成功经验,彰显出“重建图形”的解题价值,促进学生“重建图形”应用意识的形成,培养全体学生的良好解题习惯.
5规范书写,追求有序呈现
答卷是学生与阅卷老师之间对话的唯一“工具”,它是学生展示自己知识技能的“舞台”,也是老师了解学生学习状况的“平台”.近几年,网上阅卷成为了中考阅卷的主要方式.在这样的阅卷方式下,考生想要顺利完成师生之间的“对话”,呈现自己在初中阶段的学习收获,答卷的规范与工整显得特别重要.因此,模拟考试试卷讲评课上,应将“规范书写,有序呈现”作为一种解题习惯加以培养,要让学生知晓,“答卷,如同作画,要‘谋篇布局”,在工工整整呈现解题过程的前提下,应力求解答过程的有序呈现,“自左往右,从上往下”书写,决不能象画“作战图”一样将解题过程在答卷上随意“调动”.
案例5在案例4中,呈现的综合题是这次模拟考试的压轴题,题目难度较大,解题步骤很多.试卷讲评课上,笔者选择了学生解题中的部分范例进行了点评,进一步强化“规范书写,有序呈现”解题习惯的养成.现呈现一则范例的交流片断如下.
投影:一位同学的解题过程.
教师:请说说你是怎么解第(1)题的?
学生1:根据直线解析式y=3x+3,可以得到点A和点B的坐标分别为(0,3),(-1,0),由于点C是把△AOB沿y轴翻折得到的,所以C点坐标为(1,0).接下来用待定系数法分别求出“直线BD和抛物线的解析式”.
教师:不错,你说出了第(1)题的解法.说说在答题纸上,你是如何呈现解题过程的.
学生2:我先用铅笔将答题区域“自上而下”分割成宽度差不多的三块.然后,按照“自左往右,从上往下”的顺序书写解题过程.
教师:这么呈现解题过程,有什么好处呢?
学生3:答题区域的划分,让答题在限制的区域内,给人以条理清晰的感觉.
学生4:“自左往右,从上往下”书写解题过程,我们平时就是这么做的.这样呈现的解题过程,不仅写得方便,而且检查起来也很方便.我估计,这样写,阅卷老师看起来一定很舒服!
教师:很不错,这样的“有序呈现”不仅便于检查,更为老师阅卷提供了方便.在他的解题过程中,还有什么值得我们学习的呢?
学生5:解题结论的呈现很清晰,“抛物线的解析式为y=(x-3)(x-1),即y=x2-4x+3”是对前面解题过程的总结,即时呈现解题结论是很好的习惯,值得学习!
学生6:解题的过程很简洁,写出的几乎都是本题的关键步骤,失分很少.我觉得,答题时,应写出解题的关键点,不在关键点上的步骤少写,甚至可以不写.这样一来,自己写得轻松,老师批阅也舒服,减少了无谓失分!
……
在学生发表自己的见解后,笔者表扬了这位同学的“规范书写,有序呈现”的良好解习惯,对书写中的一些细节,如“自左往右,从上往下”、写关键步骤等进一步强调,要求全班同学能在考试中反复演练,保证中考时能“自动化”应用,同学们对此深表赞同.
案例分析规范书写解题过程,不仅节省了答题时间,减少了答题失误,还让阅卷老师看着舒心,批阅省心.案例显示,解题前,学生1对答题区域进行了合理“分割”,初步“圈定”了解题过程的书写范围.接下来,学生1按照“自左往右,从上往下”的顺序书写解题过程,呈现出的解题过程整齐有序,得到了很多同学的赞赏.此外,学生1给出的解题步骤直指“要害”,呈现出的都是解题的关键步骤,清晰明了地呈现出了命题者期待的每一个考点,无关步骤的“缺失”,节约了答题的空间,同时还为学生争取到了宝贵的答题时间.显然,解题范例的展示交流,唤醒了学生的解题经验,让学生体会到良好解题习惯对数学问题解决巨大作用的同时,进一步强化了“规范书写,有序呈现”的解题行为向解题习惯的转化,将学生分析问题和解决问题的能力又提升了一个档次!
解题习惯内涵十分丰富,不仅包括阅读审题的习惯,还包括思路分析、过程书写等方面的习惯,它是学生数学解题能力的重要组成部分.良好的解题习惯,是学生有效解决数学问题的保障,是有效规避解题风险的“抓手”.任何一种良好习惯的形成,都非朝夕之功,需要我们在日常教学中借助一切可用的教学契机强化培养,让学生知道怎么做,是习惯培养的第一步,鼓励学生对好的解题经验和解题行为的反复应用,是习惯养成的关键.“正向”示范,榜样引领,是习惯养成的“推进剂”.在数学课上,我们应为学生树立解题的“榜样”,让他们在观察交流中,感知到良好解题习惯的价值,逐步形成习惯养成的自觉意识,提高问题解决的成效.
以上所述,仅是笔者的一点个人感悟,不足之处,敬请批评指正!



近期,我市举行了中考模拟考试,笔者参与了试卷的批阅工作.批阅时,我们发现,一些同学因解题习惯差导致了大量失分,这让笔者十分痛心.为此,认真梳理了试卷中的“无谓失误”,并找出了与之对应的解题范例.在试卷讲评课上,对“无谓失误”精准点评的同时,还将这些规范的解题过程呈现,供学生观摩欣赏,彰显范例的“正向”示范作用.本文就结合笔者讲评中呈现的部分案例来谈谈学生应具备的五种良好解题习惯.
1审题标记,实现文图呼应
试题解答的第一关就是审题,它是学生解题的起点,也是成功解题的关键.初中数学的学科特点,决定了试题应具备学段特色和数学特色,一些试题除了有文字说明外,还配有与之对应的图形.因此,在初中阶段的数学考试中,审题绝不是简单地读题,在读的同时,我们应将文字信息中的关键词进行标记(标着重号或画线),同时,还应将文字信息在图形中对应标注,实现文图呼应,为分析和获取解题思路等做好基础性工作.
案例1如图1,点P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO等于().
A.45B.35C.43D.34
审题后如图1(说明:学生标注见图2),点P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO等于().
A.45B.35C.43D.34
案例分析这道试题条件并不多,一幅图,一段文字.这样的简单文图组合,让试题的解答看似十分简单.然而,如果不将题目中的文字信息和图形信息对应标注,这道试题的解答很可能会出现失误.事实也正如笔者所言,一些同学审题时,不仅文字中未做任何标记,连图形上也未进行标注,这样的解题习惯下选错答案并不意外.笔者呈现的这则范例中,学生审题后,将题中的几个关键信息“相切”(即题中的“切”)、“正弦”(sin)、“∠APO”等进行了标记,将“相切”通过“连接OA”和“标记直角”在图2中体现,将“OP=5,PA=4”在图中的相应线段旁进行了标注,将“∠APO”用“弧”在图中标注.这样的文图呼应,让试题条件和结论变得非常清晰,线段AO旁标注的“?”说明学生已经深刻领会了题意,并已经找到了正确的解题思路,问题很快得到化解!
2适时梳理,修正解题思路
在模拟考试和中考中,中等以上难度的试题散布在试卷的不同题型之中,这些试题常有“欲解不能,放手不甘”的感觉,解答中不可避免遇到一些“挫折”.面对此类的试题,当“解题不能”时,应及时梳理题中的条件和结论,反思解题思路分析中的得与失,发现被遗漏的条件并努力挖掘出隐含条件.这样的梳理,可以弥补“解题不能”状态下思路分析的“缺陷”,及时修正解题思路,从而找出正确的解法.
案例2试卷讲评课片断
如图3,在直角坐标系xOy中,直线y=mx与双曲线y=nx相交于点A和点B(b,-2),矩形OCDE的边CD恰好被点B平分,边DE交双曲线于F点,四边形OBDF的面积为2.求m,n的值.
教师:解答这道试题的关键是什么?
学生1:将“四边形OBDF的面积”转化为含有n的方程.
教师:怎么转化?
学生2:连接OD.根据“边CD恰好被点B平分”可得S△BOC=S△BOD=12n,根据矩形的对称性可得S△DOC=S△EOD=n,△EOF是“建构在双曲线和坐标轴上的直角三角形”,它的面积也是12n,所以,S四边形OBDF=n=2.
教师:非常棒,根据你的思路,接下来我们就可以顺利地求出m,n的值了!还有其他得到方程的方法吗?
学生陈述不同的方法,10分钟后,方法交流结束.
教师(看着学生3):老师发现你的解题过程有一些改动,解题时是不是走了一些“弯路”呀?能把你解答这道试题的经验与大家分享一下吗?
学生3:好吧!根据点的坐标的意义,我先将点B的坐标(b,-2)代入到y=nx中,得到-2=nb,整理得b=-12n,这样,我就用含有n的式子表示出了点B的坐标(-12n,-2).接下来,根据“顶点建构在坐标轴和双曲线上的直角三角形”面积求法,我用含有n的式子表示出了△BOC的面积为-12n.再往下,我有一种直觉,四边形OBDF的面积是△BOC的面积的2倍,但是我说不出理由.
教师:那你接下来是怎么做的呢?
学生3:我再读了一下题目.
教师:有什么新的发现吗?
学生3:刚才解题时,有个条件没看到.
教师:哪个条件?
学生:“CD恰好被点B平分”!这让我想到了“三角形的中线将三角形分割为两个面积相等的三角形”.所以,在连接OD后,得到了S△BOD=S△BOC=
-12n.此时,思路一下子就打开了.
教师:你还有什么发现?
学生3:△DOC和△DOE的面积相等,都是-n.我还发现了△EOF也是“顶点建构在坐标轴和双曲线上的直角三角形”,其面积也是-12n.到这儿,我发现△BOC的面积实际上与题目中所给的点B的坐标并没太大关系,所以,我删去了最初的解题过程,给出了和学生2差不多的解题过程!
教师:很好,你给我们大家做出了很好的示范!当我们解题遇到“障碍”时,就要和学生3一样,不要恐慌,重新梳理一下题目,细读文字,剖析图形,在“文图呼应”中找寻遗漏条件和隐含条件.充分利用这些条件,及时修正思路,正确的解法很快就能发现!
案例分析初次解题时,由于忽略“边CD恰好被点B平分”这一条件,让学生3的求解遇到了“障碍”,虽然写出了一些看似正确的过程,但始终无法求解.当他再度审题后,发现了这个条件,并且将它与已有知识“三角形的中线将三角形分割为两个面积相等的三角形”联系起来,找到了解题的辅助线.这样一来,“思路一下子就打开了”,隐含条件“△EOF是顶点建构在坐标轴和双曲线上的直角三角形”很快“浮出水面”,解题分析被拉回到“正道”.案例中,学生3经历了“遭遇困境—再度审题—脱困得解”的过程.事实上,每一名学生都有过这样的经历,然而能在“磨难”中形成良好的解题习惯的人却很少.基于此,在日常教学中,笔者经常会象案例2中这样,从学生的解题中挖掘出正反两面的教学资源,通过学生求解历程的自主陈述,在全班范围内分享解题的经验,突出“适时梳理”在问题解决中的作用,让这一解题行为成为学生的自觉习惯,提高学生分析问题和解决问题的能力.
3穷尽结论,力求踩点挣分
基于试题必须有一定区分度这一客观现实,与中考试题一样,模拟考试试题中也会存在一些用以控制满分的难题.因此,要求学生解答这些试题时,一定要有“宽容心”,允许自己出现无法求解的情形.作为考试,多挣分是考试的目标.试题解答时,当确实无法给出正确解题过程时,我们应尽可能多地将由条件可以得出的结论写出来,生成一些可能在“得分点”上的步骤,多少挽回一点“损失”.
案例3在分析下面这道试题时,笔者发现一些同学只给出了“零星”步骤,也得到了一些分数.
如图4,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形CDF,连接AF,DE.
(1)求证:AF=DE;(2)略.
命题者给出的第(1)题的评分标准如下:
证明:∵在梯形ABCD中,AB=CD,∴∠BAD=∠CDA(1分),∵△ABE和△DCF是等边三角形,∴AB=AE,DC=DF,∠BAE=∠CDF=60°,∴AE=DF(2分),∠EAB+∠BAD=∠FDC+∠CDA,即∠EAD=∠FDA(3分),∵AD=DA,∴△AED≌△DFA,∴AF=DE(4分).
学生1只写了一步:∵梯形ABCD中,AD∥BC,AB=CD,∴∠BAD=∠CDA.根据“评分标准”,阅卷老师给了1分.
学生2在给出学生1的过程的基础上,还增加了下面的步骤:
∵△ABE和△DCF是等边三角形,
∴AB=AE=BE=DC=DF=CF,∠BAE=∠ABE=∠AEB=∠CDF=∠CFD=∠DCF=60°.
学生2给出的解题过程,得到2分.
案例分析汽车组装车间,工人们将各种汽车零件紧密地整合在一起,就完成了一辆汽车的组装.数学解题与此类似,学生将不同的数学知识“链接”成一个整体,就形成了完整的解题过程.然而,无法回避的是,有时我们真不能将题中的所有知识“链接”起来.此时我们应告诉学生,不要灰心,出售汽车零件,同样可以实现其市场价值.数学解题亦然,数学知识也可以单独“销售获利”的.案例中的学生1,利用“等腰梯形同一底上两个底角相等”得出了“∠BAD=∠CDA”,拿到1分;学生2,不仅给出了学生1的过程,他还根据“等边三角形的三条边相等,三个角相等”得出了另外两组结论,顺利拿到2分.学生1、2紧扣题中的条件,生成的这些结论恰好都在本题的“得分点”上,阅卷老师的评判恰到好处地呈现出了这些考点的“价值”.因此,我们要鼓励学生在“解题无果”的情况下,将解题的中间过程尽可能多地呈现出来,以求踩在“得分点”上,实现所获知识的解题价值,拿到该拿的分数.
4重建图形,剔除干扰信息
数学考试中,综合问题一直都是学生解题的难点.这些试题一般包括题干和问题两部分,具有很强的综合性,信息量大,不仅包含丰富的文字信息,还有复杂的图形信息.试题一般会给出的两到三个问题,问题之间用并列或递进的方式衔接,存在着某种内在的联系.一般地,上一问题的顺利解决可能会为下一问题的求解提供一些有用的条件或共性的方法.因此,在试题解答时,不仅要从原题中捕捉有用的解题信息,还应从已经化解的数学问题中挖掘可用的条件或结论,将题目中与问题解决无关的条件剔除,简化问题情境,建构有效图形,让思路的分析和过程的书写不绕“弯子”、“干净利落”.
案例4如图5所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B,C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N,B,D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)略.
在试卷讲评时,一学生陈述了自己解答第(2)题的过程:
根据第(1)题得出的解析式和“BD与抛物线的对称轴交于点M”,求得点M的坐标为(2,1).然后,在草稿纸上作出草图,如图6.利用这幅“简图”,结合点M,C,D的坐标,我发现,△MCD是一个等腰直角三角形.根据这一发现,我在坐标轴上找到了三个符合要求的点N.在得出正确的解题思路后,回到答卷,我将符合要求的三个N点标注到答题纸的图上(即图5),并给出了完整的解题过程.
案例分析在数学考试中,复杂的问题情境,会成为很多学生解题的“障碍”.因此,为了让学生形成自主跨越“障碍”的能力,笔者将“重建图形”作为学生简化问题情境的“抓手”,通过日常教学的不断强化,促进学生形成解题应用的“惯性”.案例中,学生将与解决问题(2)无关的抛物线、抛物线的对称轴、直线AB等图形信息“剔除”,留下解题必备的“点B,D”和“△MCD”,形成图6.在无关信息被删除后,新图变得非常简单,对学生分析问题和解决问题十分有利.接下来,学生充分利用△MCD的特征,在新图中“找出了符合要求的三个点N”,并给出了完整的解题过程.这样的解题行为值得称赞,然而要想让学生能在考试中自觉生成这一行为,教师就必须通过解题教学对学生进行长期训练,训练方式很多,案例4中的求解过程的自主陈述是最常见的一种,通过分享“重建图形”解题成功经验,彰显出“重建图形”的解题价值,促进学生“重建图形”应用意识的形成,培养全体学生的良好解题习惯.
5规范书写,追求有序呈现
答卷是学生与阅卷老师之间对话的唯一“工具”,它是学生展示自己知识技能的“舞台”,也是老师了解学生学习状况的“平台”.近几年,网上阅卷成为了中考阅卷的主要方式.在这样的阅卷方式下,考生想要顺利完成师生之间的“对话”,呈现自己在初中阶段的学习收获,答卷的规范与工整显得特别重要.因此,模拟考试试卷讲评课上,应将“规范书写,有序呈现”作为一种解题习惯加以培养,要让学生知晓,“答卷,如同作画,要‘谋篇布局”,在工工整整呈现解题过程的前提下,应力求解答过程的有序呈现,“自左往右,从上往下”书写,决不能象画“作战图”一样将解题过程在答卷上随意“调动”.
案例5在案例4中,呈现的综合题是这次模拟考试的压轴题,题目难度较大,解题步骤很多.试卷讲评课上,笔者选择了学生解题中的部分范例进行了点评,进一步强化“规范书写,有序呈现”解题习惯的养成.现呈现一则范例的交流片断如下.
投影:一位同学的解题过程.
教师:请说说你是怎么解第(1)题的?
学生1:根据直线解析式y=3x+3,可以得到点A和点B的坐标分别为(0,3),(-1,0),由于点C是把△AOB沿y轴翻折得到的,所以C点坐标为(1,0).接下来用待定系数法分别求出“直线BD和抛物线的解析式”.
教师:不错,你说出了第(1)题的解法.说说在答题纸上,你是如何呈现解题过程的.
学生2:我先用铅笔将答题区域“自上而下”分割成宽度差不多的三块.然后,按照“自左往右,从上往下”的顺序书写解题过程.
教师:这么呈现解题过程,有什么好处呢?
学生3:答题区域的划分,让答题在限制的区域内,给人以条理清晰的感觉.
学生4:“自左往右,从上往下”书写解题过程,我们平时就是这么做的.这样呈现的解题过程,不仅写得方便,而且检查起来也很方便.我估计,这样写,阅卷老师看起来一定很舒服!
教师:很不错,这样的“有序呈现”不仅便于检查,更为老师阅卷提供了方便.在他的解题过程中,还有什么值得我们学习的呢?
学生5:解题结论的呈现很清晰,“抛物线的解析式为y=(x-3)(x-1),即y=x2-4x+3”是对前面解题过程的总结,即时呈现解题结论是很好的习惯,值得学习!
学生6:解题的过程很简洁,写出的几乎都是本题的关键步骤,失分很少.我觉得,答题时,应写出解题的关键点,不在关键点上的步骤少写,甚至可以不写.这样一来,自己写得轻松,老师批阅也舒服,减少了无谓失分!
……
在学生发表自己的见解后,笔者表扬了这位同学的“规范书写,有序呈现”的良好解习惯,对书写中的一些细节,如“自左往右,从上往下”、写关键步骤等进一步强调,要求全班同学能在考试中反复演练,保证中考时能“自动化”应用,同学们对此深表赞同.
案例分析规范书写解题过程,不仅节省了答题时间,减少了答题失误,还让阅卷老师看着舒心,批阅省心.案例显示,解题前,学生1对答题区域进行了合理“分割”,初步“圈定”了解题过程的书写范围.接下来,学生1按照“自左往右,从上往下”的顺序书写解题过程,呈现出的解题过程整齐有序,得到了很多同学的赞赏.此外,学生1给出的解题步骤直指“要害”,呈现出的都是解题的关键步骤,清晰明了地呈现出了命题者期待的每一个考点,无关步骤的“缺失”,节约了答题的空间,同时还为学生争取到了宝贵的答题时间.显然,解题范例的展示交流,唤醒了学生的解题经验,让学生体会到良好解题习惯对数学问题解决巨大作用的同时,进一步强化了“规范书写,有序呈现”的解题行为向解题习惯的转化,将学生分析问题和解决问题的能力又提升了一个档次!
解题习惯内涵十分丰富,不仅包括阅读审题的习惯,还包括思路分析、过程书写等方面的习惯,它是学生数学解题能力的重要组成部分.良好的解题习惯,是学生有效解决数学问题的保障,是有效规避解题风险的“抓手”.任何一种良好习惯的形成,都非朝夕之功,需要我们在日常教学中借助一切可用的教学契机强化培养,让学生知道怎么做,是习惯培养的第一步,鼓励学生对好的解题经验和解题行为的反复应用,是习惯养成的关键.“正向”示范,榜样引领,是习惯养成的“推进剂”.在数学课上,我们应为学生树立解题的“榜样”,让他们在观察交流中,感知到良好解题习惯的价值,逐步形成习惯养成的自觉意识,提高问题解决的成效.
以上所述,仅是笔者的一点个人感悟,不足之处,敬请批评指正!

