《找次品》教学例谈

    吴霞

    

    

    摘要：《找次品》为人教版数学五年级下册第八单元的教学内容，这一课虽然只将《找次品》中最简单的一类作为教学内容，但这一课并不好上，根据笔者的摸索和课堂实践，认为要做好本节课的教学，应从“抓本质”“观过程”“看练习”这三点下手，促进学生思维的发展从而达到培养学生解决问题能力的目的。

    关键词：本质 研读 过程 自主探究能力 练习 层次性

    一、透过现象抓本质，应凸显教材例题蕴含思想的研读

    本单元仅仅两个例题，麻雀虽小，但五脏俱全，两个例题承载着小学数学课标倡导的“四基”，正是例题的短而精，才让老师忽略了对教材例题蕴含思想的研读。

    如在例1的教学中，大多数老师只为了教而教，让学生说出三瓶钙片如何称一次就可以找出次品轻的一瓶。殊不知例1的教学，应透过现象看本质，抓住例题蕴含的数学思想：让学生学会从最简单、最小的数字入手寻找次品，知晓找次品的基本思路，让学生懂得通过用天平平衡的原理进行逻辑推理，完全可以确定次品是这三份中哪一份。这样安排，既引导学生用直观、简明的方式清晰地表示出推理过程：如果天平平衡……如果天平不平衡……，同时又为例2探索更多的找次品问题及“分三份”提供了認知和方法上的直观经验。

    例2的编排，不仅在例1的基础上扩大了物品数量（由3扩大到8），而且增加了关键词“至少”“保证”，有了例1简单的找次品基本推理思路做基础，教材安排小精灵直接提出“你们打算怎样表示找次品的过程”，紧接着提示了三种探索方式：

    （1）用直观图表示出推理的过程。

    （2）用表格记录不同的探索方案，以便对比、分析。

    （3）通过设疑，提出探究的线索。

    通过教材提供的这些素材，细细研读，不难发现，与例1相比，例2更能体现找次品方法的过程。在教学过程中，我们只有抓住了这个关键点，才能对症下药，采用一定的教学方法，突出重点，突破难点，从而很好地实现教学目标。

    二、透过结果观过程，应凸显学生自主探究能力的培养

    新课标指出：数学教学活动应突出学生的主体地位，教师应为学生提供合作探究和动手操作的机会，从而激发学生的学习兴趣，提高学生的数学核心素养。在本节课寻找次品“一分为三，尽量均分”环节中，我设置了以下片段：

    （一）初步建模，将待检测物品平均分成三份（当n=3时）

    先请同学们独立思考：如何在这三个物品中找出次品零件？（次品重一些）由于待检测物品的数目小以及同学们进行了简单的推理，同学们很快举起了他们的小手。紧接着我为了训练他们的语言组织能力，让他们把自己的想法对同桌说一说，并让他们相互交流，取长补短。同学们有了自己独立的思考，交流起来个个劲头十足，在反馈阶段，都一致认为先将两个待测物品分别放置在天平的两个托盘里，另一个放在天平外的想象空间托盘里，若天平平衡，则空间托盘里的物品是次品，若天平不平衡，则下沉的是次品，所以只要称一次就能找到次品。对于想象力比较差的同学，可以用手臂代替天平，既直观又创新，学生们动动脑、动动嘴、动动手就能顺利地找出次品，建立三分法模型，即把3分成三份（1、1、1）。

    （二）优化策略，尽量均分（当n=8时）

    按照以上n=3时找次品建模的三分法模型，学生很容易将8分成以下四种情况：（1、1、6），（2、2、4），（3、3、2），（4、4）。紧接着我让学生读题，帮助学生理解关键词“至少”“能保证”的含义，先让学生自己说一说，再师生一起总结：“能保证”就是指每一种找次品的方法我们都要考虑到，不能碰运气;“至少”就是指能保证找到次品的最少次数。关键词理解了，我又引导学生合作探讨：这四种方案，各称了几次？至少要称几次能保证找到次品？经过激烈的讨论交流，我们听到了以下声音：

    小组1：8（4、4）。先将8个零件放在天平的两侧，每边各4个，如果左边下沉的话，将这4个再分成两组，每边2个，再找出下沉的那一组，将其放在天平的两侧，一边放一个，下沉的便是次品，至少要称3次。

    小组2：8（3、3、2）。我们称了2次就能保证找出次品，先将天平两端各放3个零件，剩下2个，若天平平衡，将剩下的两个再称重的那个为次品;若不平衡，就将下沉的那三个再称（1、1、1），也只需称2次。（指定两名学生上黑板，一名学生解释，另一名学生画图，两名学生配合得相当好）

    小组3：我们小组也是称3次，可我们的分法跟第一组不一样，我们小组是把8分成（1、1、6）先称1次，再把6分成（2、2、2）称1次，又把2分成（1、1）称1次，所以要称3次。

    小组4：我们是把8分成（2、2、4）称1次，再把4分成（1、1、2）称1次，再把2分成（1、1）称1次，共称3次。

    听了同学们的反馈，我问道：“你们认为哪种分法用最少的次数保证一定能找出次品？”同学们经过亲身经历和实践，都异口同声地说8（3、3、2）这种方案。见学生们信心十足，我立即见机设疑：“你们能探究其中的原因吗？”给学生足够的交流时间和教学空间，让他们自主探讨、相互交流。

    生1：我认为与分的组数有关。

    生2：我认为分3组，而且尽量有2组数目一样，先在天平两端各放相同数目的物品，如果平衡，那么次品就在旁边的一份里，如果不平衡，就在下沉的那份里。

    生3：我认为分3组时，需要称的次数越少，每组的数目应该越小。

    生4：我还认为分的每组的数相差越小越好，这样每次称完，次品就被锁定在更小的数里，这样称的次数也就少了。

    有了这些精彩的课堂生成，我们不仅实现了本题的任务目标，而且还探索出找次品最优化的方案：“三分法，尽量均分”。透过结果看过程，这些基本方法和基本技能的获得，都是学生亲身经历、自主探索的结果。一个人走得很快，而一群人却可以走得很远，所以在教学的过程中，我们务必要凸显出学生自主学习的主体地位。

    三、透过检测看练习，应凸显练习设计的层次性

    练习是检验学生此节课教学目标是否达成的手段之一，练习的设计应面向全体学生，既要照顾差生，设计一些基础题，又要照顾中等生和优秀学生，设计一些有层次性和梯度性的发散性练习。如在本节课的教学中，我设计了以下三道练习：

    （一）5瓶钙片中有一瓶是次品（轻一些），完成下面找次品的过程。

    设计意图：本题是针对全体学生而设计的一道基础题，目的是巩固找次品的方法，检验教学目标是否达成。

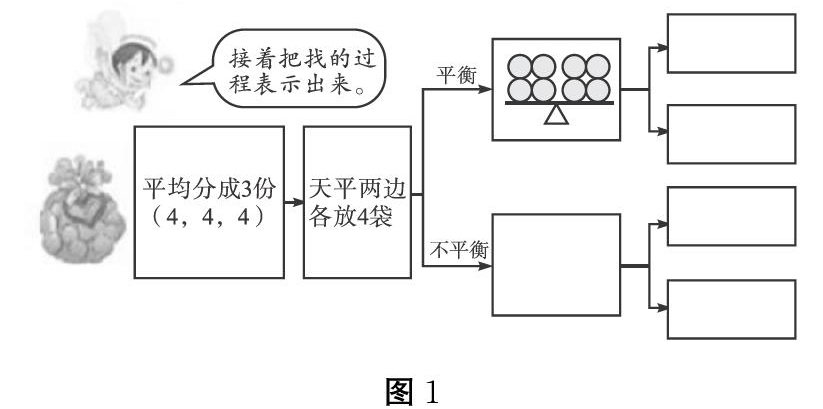
    （二）见图1。设计意图：设计此题的主要目的是检验学生是否掌握了用思维流程图直观形象地表达分析和解决找次品问题的过程，从而培养学生逻辑推理能力和思维发展能力。

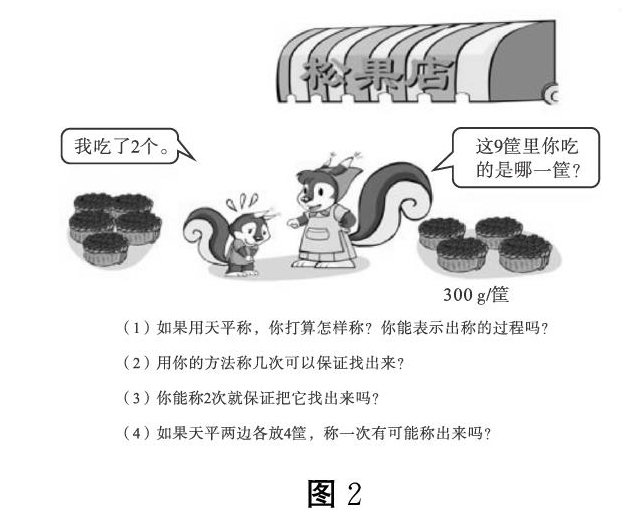
    （三）见图2。设计意图：这题与前两题相比，具有一定的梯度，（1）、（2）题主要让学生自主探究，目的是培养学生自主探索的能力，（3）题主要让学生强化用最优化的方法寻找次品，（4）题主要让学生进一步理解“保证一定能够找出次品的含义”。