紧扣比值定义 选择斜率解法
武长青

界定“线性元件和非线性元件”的标准是“元件的伏安特性曲线是否是通过坐标原点的直线”.无论是否为线性元件,电阻都按R=U/I计算,只有在线性电阻中才能用R=ΔU/ΔI.在伏安特性曲线上,电阻的倒数一定等于线上各点与原点连线的斜率,只有在线性元件中曲线的切线的斜率才等于电阻的倒数,非线性元件中曲线的切线的斜率没有意义.
1问题的提出
伏安特性曲线中如何求电阻?怎样判断电阻的变化?
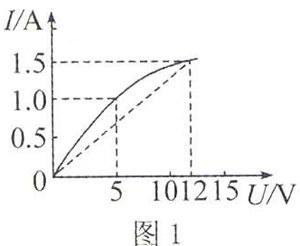
例题1某导体中的电流随其两端的电压变化,如图1实线所示,则下列说法中正确的是
A.加5 V电压时,导体的电阻是5 Ω
B.加12 V电压时,导体的电阻是8 Ω
C.由图可知,随着电压增大,导体的电阻不断减小
D.由图可知,随着电压减小,导体的电阻不断减小
实际教学过程中,学生解答中存在以下的问题:不选A和B,选择D.但部分学生选择D的解法是看伏安特性曲线的切线,切线越来越平缓,电阻越来越大.
出现以上的解法其实是源于同一思维点:“求伏安特性曲线的切线”出发.因无法求5 V、12 V时的切线所以不选A、B,对应着D答案,学生认为R=1/K,切线斜率减小,电阻值增大.这样的解法对吗?伏安特性曲线切线的斜率是电阻的倒数吗?
2紧扣定义确定正解
欧姆定律告诉我们,对于金属和电介质导电时I=U/R.变形可得R=U/I,即电阻阻值应是统一状态下电压和电流的比值.根据这样的比值定义,求出5 V时的电阻是R=5 Ω,12 V时的电阻是R=8 Ω.随着电压的增大线上各点对应的电压与电流的比值不断增大,因此电阻值增大.
3虚构模型剖析错解
学生为何会按“求伏安特性曲线的切线”的思路求解呢?这要从线性元件的伏安特性的理解上寻找根源.由于线性元件的伏安特性曲线的斜率的倒数等于线性元件的电阻.学生将“斜率”的定义进行“自然”迁移,理解成曲线斜率的倒数就是阻值的大小.同时也将线性元件的“线性”这一概念扩大成数学中的线性函数的“线性”.
数学中,线性(linear),指量与量之间按比例、成直线的关系,在数学上可以理解为一阶导数为常数的函数.由赵凯华、陈熙谋编写的高等教育出版社出版的高等学校教材《电磁学》第二版对“线性元件和非线性元件”是这样描述的:以电压U为横坐标、电流强度I为纵坐标画出的曲线,叫做该导体的伏安特性.欧姆定律成立时,伏安特性是一条通过坐标原点的直线,其斜率等于电阻R的倒数,它是一个与电压、电流无关的常量.具有这种性质的电学元件叫做线性元件,可得到界定“线性元件和非线性元件”的标准是“元件的伏安特性曲线是否是通过坐标原点的直线”.
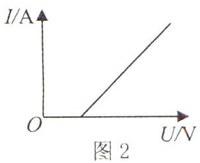
我们可以虚构以下的模型引导学生区别数学“线性”与物理“线性元件”中线性的不同.若某一元件的伏安特性如图2所示,那么该元件是线性元件吗?其阻值随着电压的增大是否改变?
从数学的认识角度出发,此图线为线性图线.认真对照线性元件的定义可知,该元件不是线性元件.
4对比分析深化理解
学生为何会将“斜率”的定义进行“自然”迁移?从授课的过程看:线性元件的伏安特性曲线是过原点的倾斜的直线,1R=k=IU,也能表达成1R=I1U1=I2U2=ΔIΔU=k.在此学生就开始知识迁移.实际上在非线性元件中,1R=I1U1≠I2U2≠ΔIΔU,即对应着(I1,U1)和(I2,U2)的电阻值并不相等.1R不能写成ΔIΔU,不能看成伏安特性曲线上该点切线的斜率,应是某点与坐标原点连线的斜率.
如图3所示,在第一个问题中当电压增大时,k2
从学生已掌握的知识看,显然与a=ΔvΔt进行了类比迁移.这其实是个错误迁移.加速度定义为△v与△t的比值.无论加速度是否恒定都是两者的比值.而电阻则是电压与电流的比值.在阻值不变的前提下,可以根据等比定理写成ΔUΔI,但这并不是电阻的定义式.
我们可以用这样的方法类比分析.在如图4所示的弹簧弹力和形变量的关系图线中,劲度系数是F与x的比值,因此实线表示随着弹簧伸长量的增大,弹簧的劲度系数先不变后减小(劲度系数应等于线上各点与原点的连线的斜率).同样,在如
图5所示的P-T图像中,虽然实线是一条倾斜的直线,但一定质量的同种气体并非做等容变化,而是体积不断减小(体积应等于线上各点与原点的连线的斜率的倒数).在如图6所示的动量-时间图像中图线上任一点切线的斜率等于该时刻物体所受的合外力(F=ΔPΔt),随时间增加合外力减小.在如图7所示的速度-时间图像中物体的加速度保持不变(a=ΔvΔt).
同为“线性”,我们应能在数学、物理范畴内区别理解.必须明确同为求斜率,是“某点与坐标原点的连线的斜率”还是“图线上某点切线的斜率”,我们应根据具体的比值定义内容选择正确、合理的解决方法.



界定“线性元件和非线性元件”的标准是“元件的伏安特性曲线是否是通过坐标原点的直线”.无论是否为线性元件,电阻都按R=U/I计算,只有在线性电阻中才能用R=ΔU/ΔI.在伏安特性曲线上,电阻的倒数一定等于线上各点与原点连线的斜率,只有在线性元件中曲线的切线的斜率才等于电阻的倒数,非线性元件中曲线的切线的斜率没有意义.
1问题的提出
伏安特性曲线中如何求电阻?怎样判断电阻的变化?
例题1某导体中的电流随其两端的电压变化,如图1实线所示,则下列说法中正确的是
A.加5 V电压时,导体的电阻是5 Ω
B.加12 V电压时,导体的电阻是8 Ω
C.由图可知,随着电压增大,导体的电阻不断减小
D.由图可知,随着电压减小,导体的电阻不断减小
实际教学过程中,学生解答中存在以下的问题:不选A和B,选择D.但部分学生选择D的解法是看伏安特性曲线的切线,切线越来越平缓,电阻越来越大.
出现以上的解法其实是源于同一思维点:“求伏安特性曲线的切线”出发.因无法求5 V、12 V时的切线所以不选A、B,对应着D答案,学生认为R=1/K,切线斜率减小,电阻值增大.这样的解法对吗?伏安特性曲线切线的斜率是电阻的倒数吗?
2紧扣定义确定正解
欧姆定律告诉我们,对于金属和电介质导电时I=U/R.变形可得R=U/I,即电阻阻值应是统一状态下电压和电流的比值.根据这样的比值定义,求出5 V时的电阻是R=5 Ω,12 V时的电阻是R=8 Ω.随着电压的增大线上各点对应的电压与电流的比值不断增大,因此电阻值增大.
3虚构模型剖析错解
学生为何会按“求伏安特性曲线的切线”的思路求解呢?这要从线性元件的伏安特性的理解上寻找根源.由于线性元件的伏安特性曲线的斜率的倒数等于线性元件的电阻.学生将“斜率”的定义进行“自然”迁移,理解成曲线斜率的倒数就是阻值的大小.同时也将线性元件的“线性”这一概念扩大成数学中的线性函数的“线性”.
数学中,线性(linear),指量与量之间按比例、成直线的关系,在数学上可以理解为一阶导数为常数的函数.由赵凯华、陈熙谋编写的高等教育出版社出版的高等学校教材《电磁学》第二版对“线性元件和非线性元件”是这样描述的:以电压U为横坐标、电流强度I为纵坐标画出的曲线,叫做该导体的伏安特性.欧姆定律成立时,伏安特性是一条通过坐标原点的直线,其斜率等于电阻R的倒数,它是一个与电压、电流无关的常量.具有这种性质的电学元件叫做线性元件,可得到界定“线性元件和非线性元件”的标准是“元件的伏安特性曲线是否是通过坐标原点的直线”.
我们可以虚构以下的模型引导学生区别数学“线性”与物理“线性元件”中线性的不同.若某一元件的伏安特性如图2所示,那么该元件是线性元件吗?其阻值随着电压的增大是否改变?
从数学的认识角度出发,此图线为线性图线.认真对照线性元件的定义可知,该元件不是线性元件.
4对比分析深化理解
学生为何会将“斜率”的定义进行“自然”迁移?从授课的过程看:线性元件的伏安特性曲线是过原点的倾斜的直线,1R=k=IU,也能表达成1R=I1U1=I2U2=ΔIΔU=k.在此学生就开始知识迁移.实际上在非线性元件中,1R=I1U1≠I2U2≠ΔIΔU,即对应着(I1,U1)和(I2,U2)的电阻值并不相等.1R不能写成ΔIΔU,不能看成伏安特性曲线上该点切线的斜率,应是某点与坐标原点连线的斜率.
如图3所示,在第一个问题中当电压增大时,k2
从学生已掌握的知识看,显然与a=ΔvΔt进行了类比迁移.这其实是个错误迁移.加速度定义为△v与△t的比值.无论加速度是否恒定都是两者的比值.而电阻则是电压与电流的比值.在阻值不变的前提下,可以根据等比定理写成ΔUΔI,但这并不是电阻的定义式.
我们可以用这样的方法类比分析.在如图4所示的弹簧弹力和形变量的关系图线中,劲度系数是F与x的比值,因此实线表示随着弹簧伸长量的增大,弹簧的劲度系数先不变后减小(劲度系数应等于线上各点与原点的连线的斜率).同样,在如
图5所示的P-T图像中,虽然实线是一条倾斜的直线,但一定质量的同种气体并非做等容变化,而是体积不断减小(体积应等于线上各点与原点的连线的斜率的倒数).在如图6所示的动量-时间图像中图线上任一点切线的斜率等于该时刻物体所受的合外力(F=ΔPΔt),随时间增加合外力减小.在如图7所示的速度-时间图像中物体的加速度保持不变(a=ΔvΔt).
同为“线性”,我们应能在数学、物理范畴内区别理解.必须明确同为求斜率,是“某点与坐标原点的连线的斜率”还是“图线上某点切线的斜率”,我们应根据具体的比值定义内容选择正确、合理的解决方法.

