分布式信源编码的压缩感知技术在无线传感器网络中的应用

    武红玉

    

    

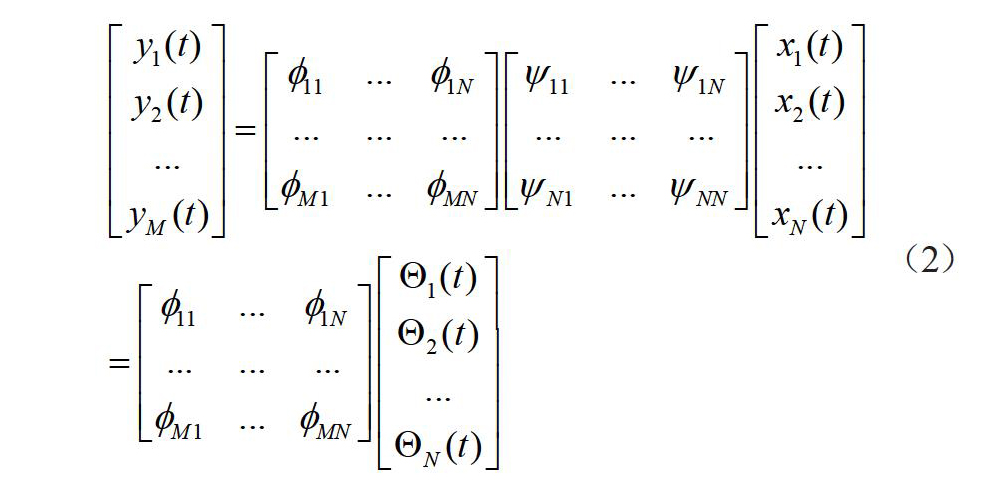
    摘 要：文章提出了分布式压缩感知理论，利用传感器节点的数据相关性，把单个信号的压缩采样扩展到信号群的压缩采样，可以实现无线传感器网络的數据重构，减少节点的通信开销，降低整个网络的能耗。

    关键词：分布式压缩感知；无线传感器网络；通信开销；能耗

    传感器技术、嵌入式计算技术、分布式信息处理技术和通信技术集合组成的无线传感器网络（Wireless Sensor Networks，WSN）是一种多跳的自组织网络，由部署在监测区域的无数具有无线通信能力的传感器节点构成，其目的主要是对被监测对象进行数据的采集和处理，并将采集的相关数据传送给网络观察者。但是发送和接受这些数据信息所消耗的能量无形中给原本能量受限的网络节点也带来压力，所以无线传感器网络的研究重点之一就是如何减少能耗。其中减少网络数据传输量是降低能耗的方法之一，因此对数据的压缩传输也是必不可少的。传统的数据压缩采用的是联合编码方式，不同于分布式信源编码，它需要节点间相互的通信来交换彼此信息，造成了额外的传感器能量的浪费，考虑到压缩感知具有比较高的压缩率，结合分布式信源编码，提出了分布式压缩感知理论，利用传感器节点的数据相关性，把单个信号的压缩采样扩展到信号群的压缩采样，可以实现无线网络的数据重构，减少节点的通信开销，降低整个网络的能耗。

    1 压缩感知理论

    美国学者Tao等[1]于2004年提出的压缩感知（Compressed Sensing，CS）是一种新的信息采集理论。如果信号满足一定条件，就可以实现信号的低速率采集与数据压缩[2-4]。美国学者Baron[5]提出的分布式压缩感知（Distributed Compressive Sensing，DCS）概念，在分布式信源编码的基础上取得了较快的发展，近几年来成了国内外研究的热点，尤其为分布式压缩感知在无线传感器的领域提供了较好的研究方向。

    传统的时域采样定理：只有当fs≥2fc时，信号经过采样后仍能恢复出原来的信号，其中fs为采样频率，fc为信号的截止频率。采用这样传统的信息处理技术，对于无线传感器网络来说，采样后的数据非常大，在对信号处理的时候，只是对其中少量的系数编码，其余大量的经过计算的小系数作为冗余信息被丢弃，这样就造成了大量的资源浪费，影响信息技术的发展，因此压缩感知理论的研究就特别有现实意义。

    在压缩感知理论中，同时对信号进行采样和压缩，则传感器的采样和计算成本大幅度降低，信号的恢复则需要合适的重构算法来实现。压缩感知处理数据的过程与传统的比较最大不同就在于在采样的过程中同时完成了数据的压缩，使得采样的数据量大大减小。尽管压缩感知以较少的采样重建原始信号，但在信号恢复过程的计算有一定复杂度，实质就是将采样的复杂度转移到了译码端的复杂度。这个方法在处理超宽度信号时，其优点就凸显出来了。

    2 压缩感知数学模型的提出

    2.1 信号的稀疏表示

    压缩感知的第一个关键问题就是信号的稀疏化表示。稀疏化的实质就是将当前域的信号通过某种变换，在其他域中的描述方法。例如时域的信号经过傅里叶变换变为频域的信号，这样处理的目的是将当前能量分散的时域信号转换为能量比较集中的频域中，更有利于信号的进一步处理。这种对信号进行变换的关系即为信号的稀疏基，也成为基字典。

    有信号理论可知，X可以用一组基Ψ=[Ψ1，…，Ψn，…，ΨN]的线性组合表示

    （1）

    其中θi=〈X，Ψi〉，θ与X是N×1矩阵，Ψ是N×N矩阵，当信号X在某个基上仅有K>>N个非零系数时，称X在Ψ上是K-稀疏的，Ψ为信号X的稀疏基。目前常用的稀疏基有正（余）弦基、小波基等。

    如果信号不具有稀疏性，首先需要对信号进行某种合适的变换，使之进行稀疏化，称为稀疏字典。反之，如果信号本身具有稀疏性，则可以从已经存在的大量系统中选择稀疏字典，比如傅里叶变换、小波变换等。信号的稀疏表示就是用尽可能少的稀疏系数保留信号的大部分有效信息，使人们更容易获取信号包含的信息，更方便进一步对信号进行加工处理，因此受到了广大研究者的关注。

    2.2 观测矩阵的设计

    压缩感知的第二个问题就是矩阵的设计问题。由压缩感知理论得知，通过投影变换到的稀疏矩阵Θ=ψTx，就需要设计一个压缩采样系统的观测器，其主要目的是从M次观测中重构出长度为N的信号X。其中，ψ为基矩阵，Θ为稀疏矩阵，为观测矩阵。M小于N。从公式（1）可以看出，如果观测过程中，X的信息破坏，信号的恢复就不可能实现。

    （2）

    因此如果观测矩阵的设计需要考虑两个问题：

    基矩阵ψ和观测矩阵的关系问题；稀疏矩阵Θ和K稀疏的信号之间的关系问题。

    3 信号的重构

    感知中第3个要素就是信号的重构，它决定了信号是否能恢复回来。相比较于奈奎斯特的局部采样，压缩感知是对所有信号的感知，可以认为是一种全局的测量。根据压缩感知理论，编码端只要少量的采样，减少了采样的能耗，但解码端承接了信号压缩带来的代价，增加了信号重构的复杂性，由此增加了更多的能量消耗，因此，信号重构算法的好坏影响到了信号压缩感知能否应用到实际环境中来。

    信号重构的算法是保证测量矩阵尽可能减少采样数据，目前重构算法的主要研究有3种[6]：

    （1）贪婪追踪算法。这类方法是通过每次迭代时选择一个局部最优解来逐步逼近原始信号。优势在于计算量小、速度快。

    （2）凸优化算法。这类方法是将非凸问题转化为凸问题求解找到信号的逼近。优点是重构效果比较好、误差小，但是计算量大。

    （3）组合算法。这类方法要求信号的采样支持通过分组测试快速重建，例如傅里叶变换、链式追踪等。

    每个算法都有优点和缺点，信号重构的主要问题就是如何构造一个稳定的、计算复杂度低的、观测数量比较少的重构算法来恢复原始信号。

    4 分布式压缩感知理论

    虽然压缩感知理论的应用比较广泛，但是在无线网络传感器方面应用的还不多，一般的压缩理论研究如何利用单节点感知数据内部的相关结构进行压缩编码，但由于无线传感器网络节点众多，以及节点有一定的存储能力，文章利用节点间的空间相关性提出了分布式压缩感知算法。

    假设S的位置为（0，0），事件区域EA内节点的位置为n（x，y），n（xr，yr）分别位于坐标（x，y），（xr，yr），信息数据S（x，y），S（xr，yr），变差函数定义为：

    （3）

    其中，（x-xr）2+（y-yr）2=r2，变差函数越小，数据的相关性就越强。在无线传感器网络监控的事件区域EA内，节点n（0，0）的信息数据S（0，0）与周围节点的数据有以下的相关性：

    （4）

    U=D表示S（0，0）由节点n（r，θ）的S（r，θ）获取，概率为1-β，U=Q表示随机变量Y获取S（0，0），概率为β。Y和Z的概率密度为fY（y），fZ（z）。

    fZ（z）可表示为： （5）

    通过对无线传感器网络监控的区域数据进行变差函数计算，从而得出时间区域EA的范围。EA范围内的节点ni（i=1，2，…，N）构成一个簇，选出节点作为簇首nh（h∈{1，2，…，N）），由nh收集EA范围内所有的感知数据Xi：Xi=Si+Ni（i=1，2，…，N），其中Si为节点ni的信息数据，Ni为独立的高斯随机变量 。下面是对EA范围内的感知数据X进行分布式压缩编码处理。

    （1）首先对X进行K项稀释获得稀释变量Θ；（2）利用QR的混沌矩阵，对Θ进行观测；（3）簇首将观测值传送给sink节点，并进行分布式压缩感知的解码处理，来重构原始信号X。

    5 结语

    本文提出的分布式压缩感知对无线传感器网络采集的数据进行压缩，有效地节省了传感器采集的能量消耗，从一定程度上也延长了传感器节点的生存周期，提高了传感器网络的带宽。