用“拆解法”破解初中数学综合题

    曹爱东

    

    

    

    摘 要：本研究提出的“拆解法”是将数学综合题化难为易、化繁为简、化整为零的一种行之有效的解题方法. 这种解题方法按照数学问题所含知识点之间的联系，通过观察、分析它们的结构特征，把综合题拆成几个贴近学生认知水平、容易解决的小问题，通过各个破解，进而解决问题. 它更符合多数学生尤其是学困生的认知水平，更好地还原难题的本来面目，让学生在拾级而上的解题过程中不断收获、不断成长，消除攻克难题的畏惧心理，体会数学学习的乐趣.

    关键词：数学解题;难题拆解;综合题破解

    美国著名数学家哈尔莫斯（Halmos，1916-）提出“数学的真正组成部分是问题和解”，而要解决越来越复杂的数学问题，除必须掌握有关数学内容的基本知识，加强必要的训练外，还需要掌握一定的解题方法. “拆解法”是将初中数学综合题化难为易、化繁为简、化整为零的一种行之有效的解题方法.

    1“拆解法”的内涵

    1.1 问题背景

    如何解答数学综合题，既是学生们在学习数学时深感头痛、苦苦探求的课题，也是教师们在工作实践中需要展开研究的课题[1].本研究者一直思索是否有一种相对应用广泛的通法可以解决所有综合题？经过多年的教学探索和实践，现在有了结果.

    1.2 理论依据

    德国数学家希尔伯特（David Hilbert，1862-1943）说过：“在讨论数学问题时，我相信特殊化比一般化起着更为重要的作用.” 可能在大多数场合，我们寻找一个问题的答案而未能成功的原因，就在于有一些比手头问题更简单、更容易的问题没有解决，或者没有完全解决. 这一切都有赖于要找出这些比较容易的问题，并能运用尽可能完善的方法和能够推广的概念来解决它们. 这种方法是克服数学困难的重要的杠杆之一.

    著名美国数学家和数学教育家波利亚（George Polya，1887～1985）在《怎样解题》一书中说：“如果你不能解决所提出的问题，那么可先去解决一个更特殊的问题或解决这个问题的一部分.”

    我国数学家华罗庚（1910-1985）也强调：解题时先足够地退，退到我们最易看清楚问题的地方，认透了、鉆深了，然后再上去[2].

    基于以上了解，并根据方法论的基本原理和数学解题的基本思想、基本方法，我们可以使用“拆解法”将综合题分成几个小问题，按层次解决.

    1.3 定义、适用原则及范围

    定义：所谓“拆解法”就是按照数学问题所含知识点之间的联系，通过观察、分析它们的结构特征，把综合题拆成几个贴近学生认知水平、容易解决的小问题，化整为零，通过各个破解，进而解决问题的一种数学解题方法.

    原则：在熟悉数学基础知识和掌握基本解题方法的基础上运用“拆解法”.

    范围：所有的中等难度及压轴试题都适用，适用于所有层次学生的学习，特别是学困生.

    1.4 目的、方法与意义

    目的：有利于夯实双基，提炼典型的思维方法，让解题思路更具体、更清晰、更有条理性，使复杂问题简单化，有效提高学生的综合解题能力.

    方法：把复杂问题分拆成若干个简单的问题，然后各个击破.

    意义：操作性强、应用范围广、适用学生多，尤其为学困生低起点、高输出解决综合题提供可能.

    2 “拆解法”的应用举例

    2.1 试题呈现

    题目 （2019年北京中考第27题）已知∠AOB=30°，点H为射线OA上一定点，OH=3+1，点P为射线OB上一点，点M为线段OH上一动点，连接PM，满足∠OMP为钝角，以点P为中心，将线段PM顺时针旋转150°，得到线段PN，连接ON.

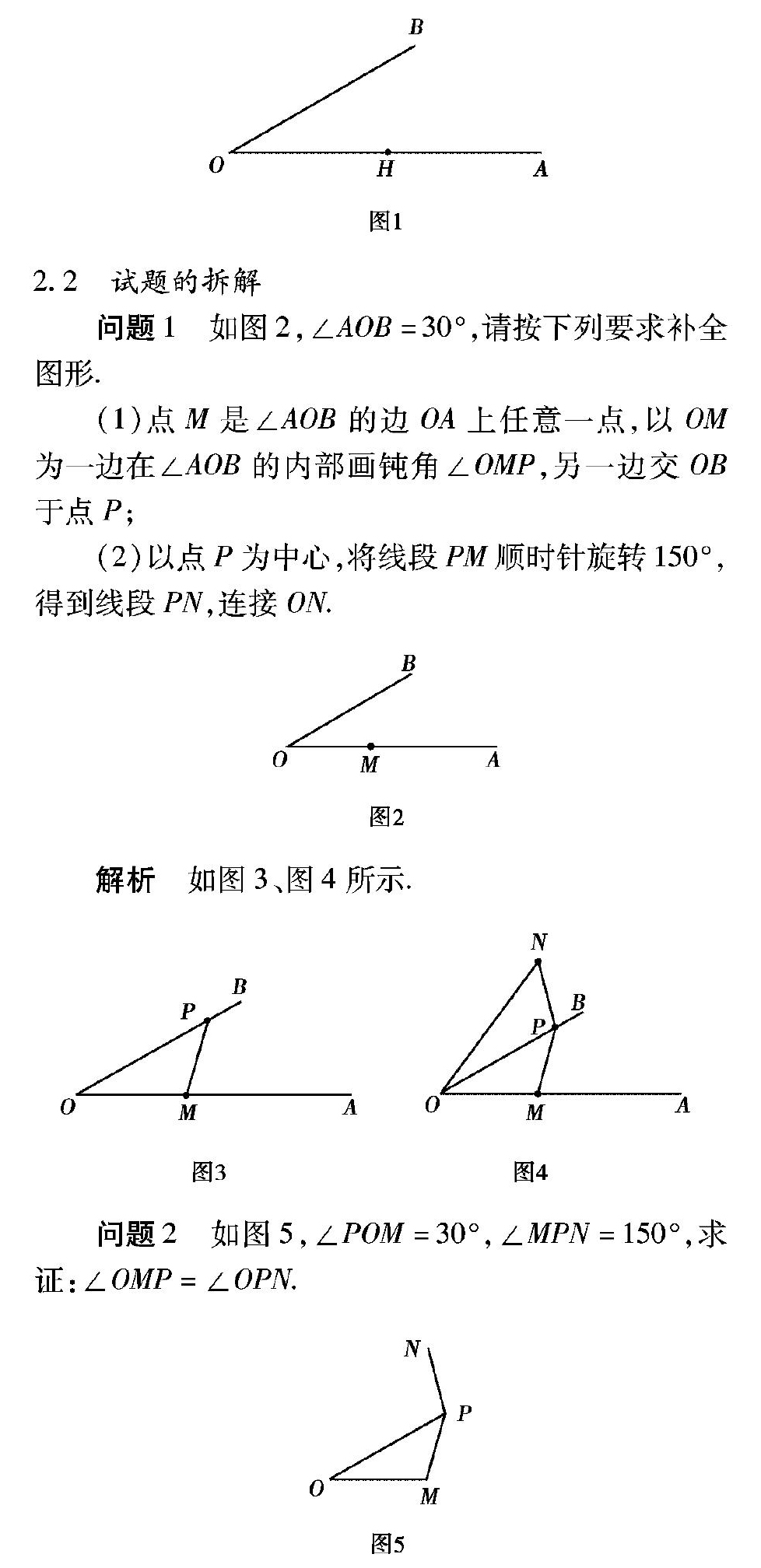
    （1）依题意补全图1;

    （2）求证：∠OMP=∠OPN;

    （3）点M关于点H的对称点为点Q，连接QP.写出一个OP的值，使得对于任意的点M总有ON=QP，并证明.